Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Zadania z treścią/Prędkość/1 ruchomy obiekt

Wyszukiwanie zadań

Rowerzysta jedzie z miejscowości 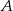A do odległej o 48 km miejscowości 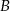B . Gdyby zwiększył swoją prędkość o x kilometrów na godzinę, to jechałby 4 godziny, gdyby zaś zmniejszył swoją prędkość o x kilometrów na godzinę, to jechałby 6 godzin. Wyznacz prędkość rowerzysty.

Syzyf codziennie stoi przed zadaniem wtoczenia ciężkiej kamiennej kuli na szczyt pewnej góry.

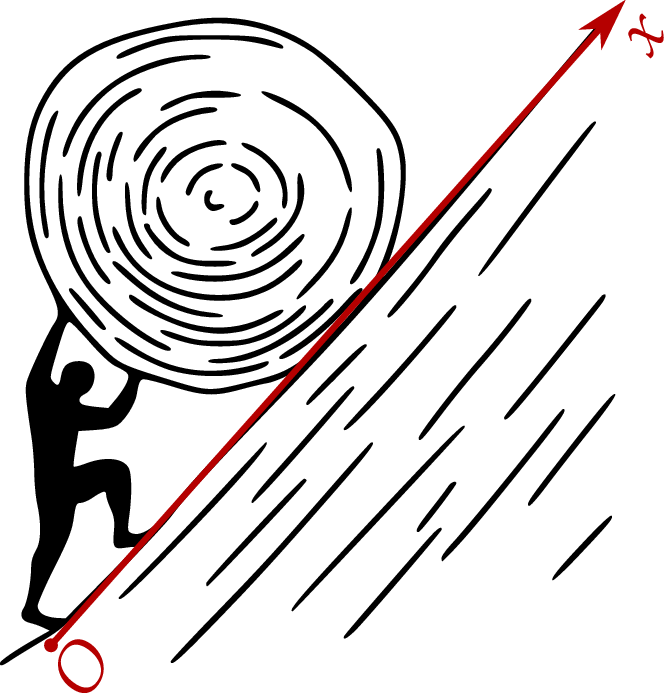
ZINFO-FIGURE

W chwili 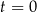t = 0 znajduje się on w punkcie 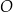O oddalonym od szczytu o 4 km, a położenie x Syzyfa wtaczającego kulę jest opisane zależnością

x (t) = −t3 + 16,5t2 + 180t dla t ∈ [0,24],

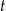gdzie x jest wyrażone w metrach, a t – w godzinach. Oś 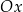Ox jest skierowana do wierzchołka góry i jest styczna w każdym punkcie do zbocza góry. Oblicz najmniejszą odległość, na jaką Syzyf zbliży się do wierzchołka góry, oraz największą prędkość, z jaką wtacza kamień pod górę.

Motocyklista drogę z miasta 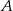A do miasta 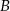B pokonał ze średnią prędkością 84 km/h. Pokonanie drogi powrotnej zajęło mu o godzinę dłużej, a średnia prędkość wyniosła 56 km/h. Oblicz odległość między miastami 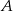A i B .

Ukryj Podobne zadania

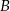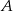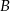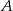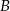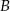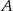Miejscowości A i B są połączone linią kolejową. Pociąg przebywa trasę z A do B ze średnią prędkością 80 km/h. W drodze powrotnej średnia prędkość pociągu jest większa o 20 km/h i dzięki temu pociąg pokonuje trasę od B do A w czasie o godzinę krótszym. Jaka jest długość linii kolejowej między miejscowościami 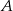A i B ?

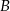Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 km/h mniejsza od średniej prędkości, z jaką schodził ze wzgórza.

Ukryj Podobne zadania

Turysta zwiedzał zabytkowy młyn stojący w dolinie rzeki. Droga łącząca parking z młynem ma długość 1,8 km. Łączny czas wędrówki turysty z parkingu do młyna i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 54 minuty. Oblicz, z jaką średnią prędkością turysta schodził w dolinę, jeżeli prędkość ta była o 0,9 km/h większa od średniej prędkości, z jaką wracał na parking.

Codzienna trasa listonosza ma kształt trójkąta równobocznego, którego wierzchołki stanowią bloki 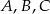A ,B,C . Z bloku 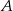A do bloku 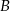B listonosz idzie z prędkością 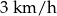3 km/h . Z bloku 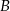B do bloku 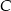C idzie z prędkością dwukrotnie większą. Średnia prędkość na całej trasie jest równa 4 km/h. Oblicz, z jaką średnią prędkością listonosz porusza się od bloku 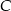C do bloku A .

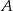Szkolne koło turystyczne zorganizowało dla swoich członków pieszą wycieczkę po okolicach Łodzi. Grupa wyszła o godz. 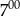700 . W ciągu pierwszych dwóch godzin turyści przeszli 8 km. Następnie przez 1,5 godziny odpoczywali w lesie. Do celu wędrówki pozostała trasa, którą grupa pokonała w ciągu 2 godzin idąc z prędkością 3 km/h. Po półgodzinnym ponownym odpoczynku turyści udali się w drogę powrotną do Łodzi, idąc z prędkością 2 km/h.

  • Narysuj wykres funkcji przyporządkowującej czasowi wędrówki (w godzinach) odległość turystów (w kilometrach) od Łodzi.
  • Ile łącznie kilometrów przebyła grupa turystów?
  • Podaj średnią prędkość marszu turystów na całej trasie.
  • O której godzinie turyści dotarli do Łodzi?

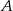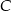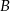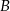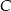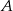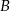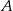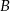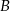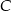Pan Michał jechał z miejscowości A do miejscowości C przez miejscowość B . Droga z B do C jest o 60 km dłuższa niż droga z A do B . Trasę pomiędzy miejscowościami A i B pan Michał pokonał ze średnią prędkością 70 km/h. Z miejscowości B do C jechał średnio 90 km/h. Średnia prędkość całego przejazdu wyniosła 80 km/h. Jaką drogę przejechał pan Michał z 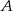A do C ?

Ukryj Podobne zadania

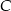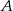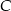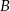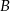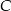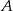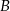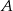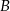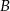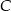Pan Piotr jechał z miejscowości A do miejscowości C przez miejscowość B . Droga z B do C jest o 80 km dłuższa niż droga z A do B . Trasę pomiędzy miejscowościami A i B pan Piotr pokonał ze średnią prędkością 60 km/h. Z miejscowości B do C jechał średnio 80 km/h. Średnia prędkość całego przejazdu wyniosła 70 km/h. Jaką drogę przejechał pan Piotr z 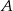A do C ?

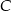Samochód przejechał 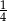1 4 trasy ze średnią prędkością 80 km/h. Na całej trasie średnia prędkość samochodu była równa 64 km/h.Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.

Ukryj Podobne zadania

Samochód przejechał połowę trasy ze średnią prędkością 40 km/h. Na całej trasie średnia prędkość samochodu była równa 48 km/h. Oblicz z jaką średnią prędkością samochód przejechał pozostałą część trasy.

W czasie wycieczki rowerowej uczniowie mieli do przebycia trasę długości 84 km. Podzielili tę trasę na odcinki równej długości i codziennie przejeżdżali wyznaczony odcinek. Gdyby na przebycie całej trasy zużyli o dwa dni więcej, to mogliby dziennie przejeżdżać o 7 km mniej. Ile kilometrów przebywali uczniowie dziennie i ile dni potrzebowali na pokonanie trasy?

Ukryj Podobne zadania

Pewien turysta pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.

Gąsienica pełźnie po gałęzi do najbliższego smakowitego liścia, który jest odległy o 63,5 cm. Gąsienica jest jednak osłabiona i pełznie coraz wolniej. W pierwszej minucie udało jej się przebyć 32 cm, w drugiej pokonała drogę długości 16 cm, w trzeciej przepełznęła 8 cm itd. Po ilu minutach gąsienica dopełznie do liścia?

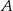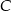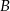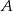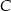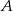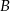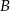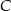Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości A do miejscowości C przez miejscowość B , która znajduje się w połowie drogi z A do C . Wartość prędkości średniej samochodu na trasie z A do B była równa 40 km/h, a na trasie z B do C – 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 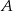A do C .

Ukryj Podobne zadania

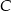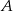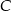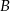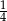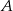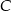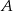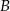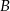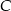Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości A do miejscowości C przez miejscowość B , która znajduje się w 14 drogi z A do C . Wartość prędkości średniej samochodu na trasie z A do B była równa 80 km/h, a na trasie z B do C – 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 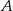A do C .

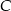Pociąg osobowy mija obserwatora w ciągu 5 s, a obok peronu długości 300 m przejeżdża w ciągu 25 s.

  • Oblicz długość pociągu i jego prędkość.
  • Określ, jak długo pociąg będzie mijał pociąg towarowy długości 150 m jadący równoległym torem w przeciwnym kierunku z prędkością 36 km/h.

Stasiu wybrał się na spacer po lesie. Na wykresie przedstawiono przebytą przez niego drogę w zależności od czasu.

PIC

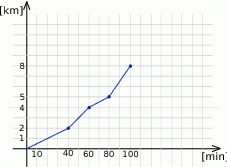
  • Oblicz z jaką średnią prędkością poruszał się w trakcie spaceru. Wynik podaj w kilometrach na godzinę.
  • W której minucie spaceru przebył dokładnie połowę drogi?
  • Z jaką największą, i z jaką najmniejszą prędkością się poruszał? Wynik podaj w kilometrach na godzinę.

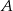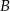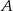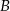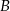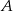Pomiędzy miastami A i B kursuje autobus. Droga między tymi miastami prowadzi przez wzgórze. Autobus jadąc pod górę rozwija prędkość 25 km/h, a z góry 50 km/h. Podróż z A do B trwa 3,5 h, a z B do A 4 h. Jaka jest odległość z 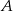A do B ?

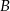Rowerzysta w ciągu pierwszej godziny przejechał 21 km, a w ciągu każdej następnej godziny – odcinek o 0,75 km krótszy od poprzedniego. Jaką drogę pokonał rowerzysta i w jakim czasie, jeśli w ciągu ostatniej godziny przejechał 18 km?

Rowerzysta jedzie ze stałą prędkością 20km/h.

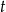  • Napisz wzór wyrażający drogę s rowerzysty w ciągu t godzin.
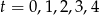  • Sporządź tabelkę wartości s dla t = 0,1,2,3,4 .
  • Naszkicuj wykres zależności s od t .

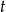Kuba pożyczył od taty samochód, którym wyruszył z domu na spotkanie ze swoją dziewczyną. Przed wyjazdem obliczył, że jadąc ze średnią prędkością 60 km/h przybędzie na spotkanie dokładnie o umówionej godzinie. Po przejechaniu (z zaplanowaną prędkością) 60% drogi "złapał gumę", a zmiana koła zajęła mu 16 minut. Teraz, aby zdążyć na spotkanie, musiałby jechać z prędkością 120 km/h. Oblicz odległość od domu Kuby do miejsca spotkania z ukochaną.

Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.

Ukryj Podobne zadania

Po zmodernizowaniu linii kolejowych przeciętna prędkość pociągów ekspresowych kursujących na 400-kilometrowej trasie wzrosła o 20 km/godz, a czas podróży skrócił się o godzinę. Oblicz, z jaką średnia prędkością jeżdżą obecnie pociągi ekspresowe na tej trasie.

Turysta przeszedł trasę długości 24 km ze stałą prędkością. Gdyby prędkość tę zwiększył o 1,2 km/h, to tę samą drogę przeszedłby w czasie o 1 godzinę krótszym. Oblicz rzeczywistą prędkość turysty i czas, w którym przebył trasę.

Samochód przebył w pewnym czasie 210 km. Gdyby jechał o pół godziny krócej to średnia prędkość z jaką przejechał tę trasę byłaby większa o 10 km/h. Oblicz, z jaką średnią prędkością jechał ten samochód.

Samochód przejechał trasę długości 84 km. Gdyby jechał ze średnią prędkością większą o 12 km/h, to przejechałby tę trasę w czasie o 21 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten samochód.

Kierowca obliczył, że trasę 220 km pokona w czasie 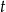t , jeśli będzie jechał ze średnią prędkością v . Wyjechał o 20 minut później niż zamierzał, więc aby dojechać na zaplanowaną godzinę, musiał zwiększyć prędkość o 5 km/h. Oblicz średnią prędkość z jaką planował jechać kierowca.

Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 36 minut.

Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

Pewien kierowca, jadąc z miasta 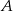A do miasta 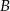B , zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta 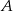A , jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?

Grupa rowerzystów jechała ze stałą prędkością do miasta oddalonego o 120 km. Gdyby jechali ze średnią prędkością o 5 km/godz. większą, to przejechaliby tę odległość w czasie o 2 godziny krótszym. Wyznacz średnią prędkość grupy i czas przejazdu.

Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 24 minut.

Kolarz przejechał trasę długości 60 km. Gdyby jechał ze średnią prędkością większą o 1 km/h, to przejechałby tę trasę w czasie o 6 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 60 km. Jadąc z domu nad jezioro poruszał się z prędkością o 2 km/h większą niż w drodze powrotnej i pokonał trasę w czasie o 10 minut krótszym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 80 km. Jadąc z domu nad jezioro poruszał się z prędkością o 4 km/h mniejszą niż w drodze powrotnej i pokonał trasę w czasie o 20 minut dłuższym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?

Rejsowy samolot z Warszawy do Rzymu przelatuje nad Austrią każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. We wtorek jego średnia prędkość była o 10% większa niż prędkość przelotowa, a w czwartek średnia prędkość była o 10% mniejsza od zakładanej prędkości przelotowej. Czas przelotu nad Austrią w czwartek różnił się od wtorkowego o 12 minut. Jak długo trwał przelot tego samolotu nad Austrią we wtorek?

Ukryj Podobne zadania

Pociąg pokonuje każdorazowo trasę pomiędzy Katowicami i Łodzią z taką samą zakładaną średnią prędkością. Pewnego dnia pociąg pokonał tę trasę w czasie o 10% krótszym od zakładanego, a następnego dnia w czasie o 15% dłuższym od zakładanego. Różnica prędkości średnich w tych dwóch dniach wyniosła 25 km/h. Ile wynosi zakładana średnia prędkość z jaką pociąg towarowy pokonuje trasę między Katowicami a Łodzią?

Rejsowy samolot z Warszawy do Paryża przelatuje nad Niemcami każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. W poniedziałek jego średnia prędkość była o 20% mniejsza niż prędkość przelotowa, a w środę średnia prędkość była o 20% większa od zakładanej prędkości przelotowej. Czas przelotu nad Niemcami w poniedziałek różnił się od czasu przelotu w środę o 28 minut. Jak długo trwał przelot tego samolotu nad Niemcami w poniedziałek?

Koszt godziny pływania pewnego rodzaju łodzi jest sumą kosztu stałego i kosztu zmiennego zależnego od prędkości łodzi. Wiadomo, że koszt stały jest równy 2880 zł/h, a koszt zmienny 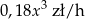0,18x 3 zł/h , gdzie 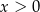x > 0 oznacza prędkość łodzi (w km/h).

  • Przy jakich prędkościach łodzi koszt przepłynięcia 1 km będzie mniejszy niż 306 zł?
  • Przy jakiej prędkości łodzi koszt przepłynięcia 1 km będzie najmniejszy? Oblicz ten koszt.
Strona 1 z 2