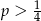Ze zbioru kolejnych liczb naturalnych 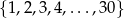 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 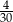 B)
B) 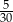 C)
C) 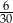 D)
D) 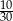
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Zbiory liczb
Ze zbioru kolejnych liczb naturalnych 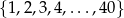 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 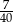 B)
B) 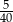 C)
C) 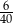 D)
D) 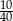
Ze zbioru kolejnych liczb naturalnych 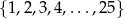 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
A) 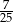 B)
B) 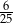 C)
C) 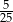 D)
D) 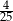
Ze zbioru 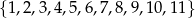 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 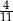 B)
B) 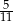 C)
C) 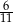 D)
D) 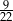
Ze zbioru liczb 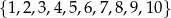 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru 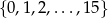 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 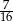 B)
B)  C)
C) 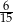 D)
D) 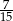
Ze zbioru 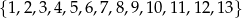 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 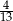 B)
B) 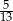 C)
C) 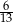 D)
D) 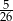
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 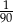 B)
B) 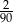 C)
C) 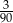 D)
D) 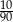
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 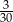 B)
B) 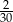 C)
C) 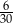 D)
D) 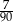
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 50 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 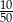 B)
B) 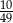 C)
C) 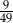 D)
D) 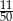
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 40 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 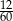 B)
B) 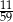 C)
C) 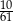 D)
D) 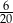
Ze zbioru dzielników naturalnych liczby 8 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 4 jest równe
A) 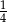 B)
B) 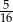 C)
C) 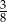 D)
D) 
Ze zbioru dzielników naturalnych liczby 12 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 6 jest równe
A) 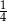 B)
B) 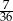 C)
C) 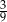 D)
D) 
Ze zbioru 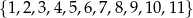 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 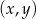 , gdzie
, gdzie  jest pierwszą wylosowaną liczbą,
jest pierwszą wylosowaną liczbą, 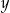 jest drugą wylosowaną liczbą. Wszystkich par
jest drugą wylosowaną liczbą. Wszystkich par 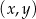 takich, że suma
takich, że suma 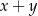 jest liczbą parzystą jest
jest liczbą parzystą jest
A) 20 B) 25 C) 50 D) 61
Losujemy jedną liczbę ze zbioru 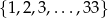 . Niech
. Niech 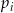 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 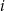 przy dzieleniu przez 10. Wtedy
przy dzieleniu przez 10. Wtedy
A) 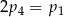 B)
B) 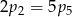 C)
C) 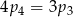 D)
D) 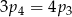
Losujemy jedną liczbę ze zbioru 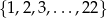 . Niech
. Niech 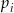 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 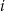 przy dzieleniu przez 4. Wtedy
przy dzieleniu przez 4. Wtedy
A) 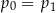 B)
B) 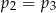 C)
C) 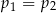 D)
D) 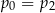
Ze zbioru liczb 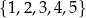 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb mniejszych od 4 jest równe prawdopodobieństwu wylosowania dwóch liczb większych od 2. | P | F |
Prawdopodobieństwo tego, że pierwsza liczba jest większa od drugiej jest równe 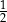 . . | P | F |
Ze zbioru liczb naturalnych pięciocyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 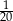 C)
C) 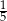 D)
D) 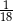
Ze zbioru liczb naturalnych zawartych w przedziale 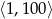 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 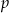 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
A) 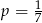 B)
B) 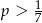 C)
C) 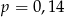 D)
D) 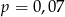
Ze zbioru liczb naturalnych zawartych w przedziale 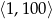 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 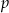 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 6. Wówczas
A) 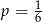 B)
B) 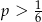 C)
C) 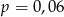 D)
D) 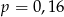
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 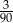 B)
B) 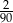 C)
C) 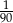 D)
D) 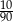
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 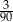 B)
B) 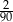 C)
C) 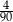 D)
D) 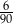
Ze zbioru liczb całkowitych, które są zawarte w przedziale 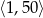 losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
A) 0,0048 B) 0,0028 C) 0,0024 D) 0,0052
Ze zbioru pięćdziesięciu kolejnych liczb naturalnych od 1 do 50 losujemy dwie liczby  i
i 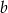 takie, że
takie, że 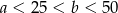 . Prawdopodobieństwo, że liczba
. Prawdopodobieństwo, że liczba 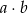 jest podzielna przez 50 jest równe
jest podzielna przez 50 jest równe
A) 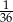 B)
B) 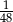 C)
C) 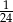 D)
D) 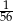
Ze zbioru kolejnych liczb naturalnych  losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 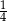 B)
B) 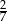 C)
C) 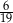 D)
D) 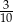
Ze zbioru kolejnych liczb naturalnych 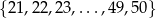 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
A) 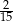 B)
B)  C)
C) 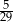 D)
D) 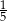
Ze zbioru liczb 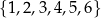 losujemy dwa razy po jednej liczbie ze zwracaniem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
losujemy dwa razy po jednej liczbie ze zwracaniem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb, których suma dzieli się przez 9 jest większe od 0,1. | P | F |
| Prawdopodobieństwo tego, że pierwsza liczba dzieli drugą jest mniejsze niż 0,38. | P | F |
Z każdego ze zbiorów 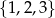 i
i 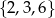 wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech
wybieramy po jednej liczbie i obliczamy ich iloczyn. Niech 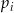 będzie prawdopodobieństwem otrzymania
będzie prawdopodobieństwem otrzymania 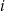 w wyniku tego działania. Wtedy
w wyniku tego działania. Wtedy
A) 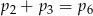 B)
B) 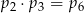 C)
C) 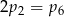 D)
D) 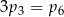
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że w zapisie dziesiętnym wylosowanej liczby jest dokładnie jedna cyfra 3?
A) 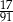 B)
B) 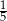 C)
C) 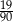 D)
D) 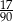
Spośród wszystkich liczb dwucyfrowych dodatnich losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 20 jest równe
A) 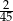 B)
B) 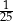 C)
C) 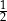 D)
D) 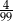
Ze zbioru cyfr 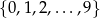 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
A) 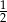 B)
B) 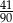 C)
C)  D)
D) 
Ze zbioru cyfr 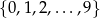 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
A) 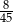 B)
B) 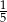 C)
C)  D)
D) 
Ze zbioru cyfr 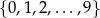 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wyjęte w kolejności losowania cyfry utworzą liczbę nieparzystą, jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wyjęte w kolejności losowania cyfry utworzą liczbę nieparzystą, jest równe
A)  B)
B) 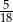 C)
C) 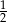 D)
D) 
Ze zbioru 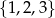 wybieramy dwie liczby (mogą się powtarzać), a ze zbioru
wybieramy dwie liczby (mogą się powtarzać), a ze zbioru 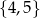 jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
jedną liczbę. Na ile sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
A) 2 B) 3 C) 4 D) 6
Ze zbioru liczb naturalnych dwucyfrowych nie większych niż 35 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 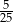 B)
B) 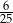 C)
C) 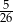 D)
D) 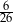
Ze zbioru liczb 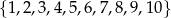 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby parzystej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb 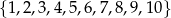 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby podzielnej przez 3 lub 4 jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 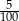 C)
C) 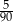 D)
D) 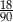
Ze zbioru kolejnych liczb naturalnych 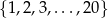 losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
losujemy jedną liczbę. Prawdopodobieństwo, że wylosujemy liczbę podzielną przez 3 jest równe
A) 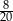 B)
B) 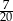 C)
C) 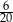 D)
D) 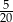
Ze zbioru liczb 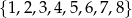 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 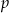 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 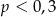 B)
B) 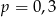 C)
C) 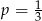 D)
D) 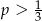
Ze zbioru liczb 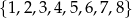 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 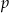 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 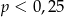 B)
B) 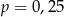 C)
C) 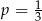 D)
D) 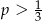
Ze zbioru liczb 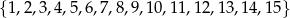 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 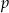 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 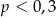 B)
B) 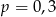 C)
C) 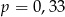 D)
D) 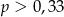
Ze zbioru liczb 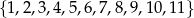 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 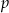 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 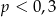 B)
B) 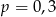 C)
C) 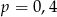 D)
D) 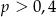
Ze zbioru 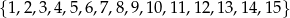 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 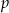 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 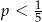 B)
B) 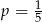 C)
C) 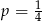 D)
D)