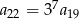Dany jest ciąg geometryczny 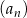 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 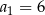 . Jeżeli
. Jeżeli 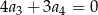 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 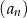 jest
jest
A) 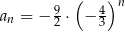 B)
B) 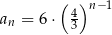 C)
C) 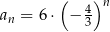 D)
D) 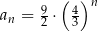
/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny/Różne
Dany jest ciąg geometryczny 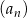 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 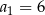 . Jeżeli
. Jeżeli 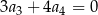 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 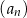 jest
jest
A) 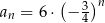 B)
B) 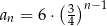 C)
C) 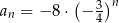 D)
D) 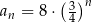
W rosnącym ciągu geometrycznym stosunek wyrazu czwartego do drugiego jest równy 8. Iloraz tego ciągu jest równy
A) 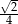 B) 4 C)
B) 4 C) 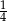 D)
D) 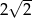
Dany jest ciąg geometryczny 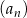 , określony dla
, określony dla 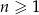 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 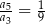 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 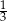 B)
B) 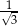 C) 3 D)
C) 3 D) 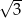
Dany jest ciąg geometryczny 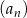 , określony dla
, określony dla 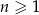 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 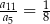 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 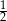 B)
B) 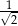 C)
C) 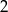 D)
D) 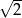
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 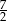 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 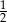 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 1 C) -0,25 D) -1
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 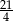 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 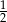 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) 0,75 C) 0,375 D) -0,75
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 39. Iloraz tego ciągu jest równy 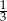 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 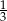 B) 1 C)
B) 1 C) 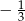 D) 3
D) 3
Trzy liczby tworzą ciąg geometryczny. Iloczyn tych liczb jest równy 216. Drugi wyraz tego ciągu jest równy
A) 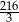 B) 6 C) 36 D) 12
B) 6 C) 36 D) 12
Trzy liczby tworzą ciąg geometryczny. Iloczyn tych liczb jest równy 125. Drugi wyraz tego ciągu jest równy
A) 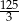 B) 75 C) 25 D) 5
B) 75 C) 25 D) 5
Trzy liczby tworzą ciąg geometryczny. Iloczyn tych liczb jest równy 64. Drugi wyraz tego ciągu jest równy
A) 4 B) 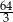 C) 16 D) 32
C) 16 D) 32
Suma trzech pierwszych wyrazów malejącego ciągu geometrycznego jest równa 10,5. Drugi wyraz tego ciągu jest równy 3. Czwarty wyraz tego ciągu jest równy
A) 1,5 B) 3,5 C) 0,75 D) 2,25
Dany jest nieskończony rosnący ciąg geometryczny 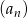 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 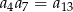 B)
B) 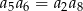 C)
C) 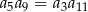 D)
D) 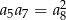
Pięć liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 59049. Trzeci wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Siedem liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 2187. Czwarty wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Ciąg geometryczny 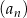 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 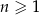 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 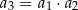 . Niech
. Niech 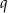 oznacza iloraz ciągu
oznacza iloraz ciągu 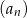 . Wtedy
. Wtedy
A) 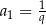 B)
B) 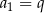 C)
C) 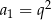 D)
D) 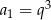
Ciąg geometryczny 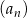 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 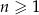 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 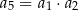 . Niech
. Niech 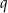 oznacza iloraz ciągu
oznacza iloraz ciągu 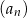 . Wtedy
. Wtedy
A) 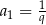 B)
B) 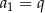 C)
C) 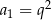 D)
D) 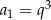
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 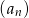 jest określona wzorem
jest określona wzorem 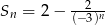 . Wtedy iloraz
. Wtedy iloraz 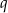 tego ciągu jest równy
tego ciągu jest równy
A) 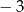 B)
B) 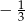 C)
C) 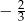 D)
D) 
Dany jest nieskończony rosnący ciąg geometryczny 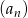 o wyrazach dodatnich, gdzie
o wyrazach dodatnich, gdzie 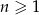 . Wtedy
. Wtedy
A) 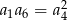 B)
B) 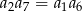 C)
C) 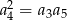 D)
D) 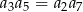
W rosnącym ciągu geometrycznym 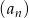 , określonym dla
, określonym dla 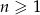 , spełniony jest warunek
, spełniony jest warunek 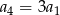 . Iloraz
. Iloraz 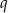 tego ciągu jest równy
tego ciągu jest równy
A) 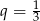 B)
B) 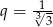 C)
C) 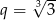 D)
D) 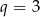
W rosnącym ciągu geometrycznym 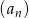 , określonym dla
, określonym dla 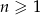 , spełniony jest warunek
, spełniony jest warunek 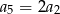 . Iloraz
. Iloraz 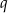 tego ciągu jest równy
tego ciągu jest równy
A) 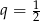 B)
B) 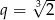 C)
C) 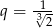 D)
D) 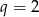
Ciąg geometryczny 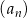 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 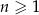 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 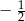 . Wtedy
. Wtedy
A) 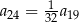 B)
B) 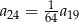 C)
C) 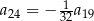 D)
D) 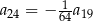
W rosnącym ciągu geometrycznym 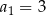 oraz
oraz 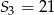 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 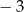 B)
B) 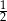 C) 2 D) 3
C) 2 D) 3
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 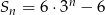 , gdzie
, gdzie 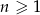 , to czwarty wyraz tego ciągu jest równy
, to czwarty wyraz tego ciągu jest równy
A) 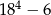 B) 480 C) 324 D) 156
B) 480 C) 324 D) 156
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 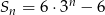 , gdzie
, gdzie 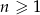 , to trzeci wyraz tego ciągu jest równy
, to trzeci wyraz tego ciągu jest równy
A) 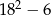 B) 108 C) 324 D) 156
B) 108 C) 324 D) 156
Jeżeli suma częściowa ciągu geometrycznego wyraża się wzorem 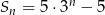 , gdzie
, gdzie 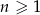 , to czwarty wyraz tego ciągu jest równy
, to czwarty wyraz tego ciągu jest równy
A) 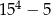 B) 270 C) 400 D) 130
B) 270 C) 400 D) 130
Wszystkie wyrazy ciągu geometrycznego 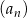 określonego dla
określonego dla 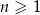 są dodatnie i
są dodatnie i 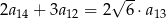 . Stąd wynika, że iloraz
. Stąd wynika, że iloraz 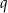 tego ciągu jest równy
tego ciągu jest równy
A) 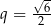 B)
B) 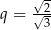 C)
C) 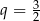 D)
D) 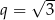
W rosnącym ciągu geometrycznym 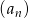 , określonym dla
, określonym dla 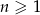 , spełniony jest warunek
, spełniony jest warunek 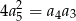 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 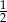 B)
B) 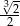 C)
C) 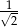 D)
D) 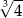
W rosnącym ciągu geometrycznym 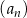 , określonym dla
, określonym dla 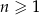 , spełniony jest warunek
, spełniony jest warunek 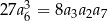 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 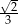 B)
B) 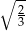 C)
C)  D)
D) 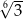
Dany jest nieskończony rosnący ciąg geometryczny 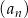 o wyrazach dodatnich. Iloraz
o wyrazach dodatnich. Iloraz 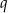 tego ciągu jest jednym z pierwiastków równania kwadratowego
tego ciągu jest jednym z pierwiastków równania kwadratowego 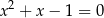 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia
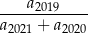
jest równa
A) 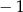 B)
B) 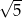 C)
C) 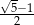 D) 1
D) 1
Który z podanych ciągów jest ciągiem geometrycznym?
A) 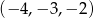 B)
B) 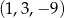 C)
C) 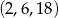 D)
D) 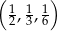
Dany jest nieskończony ciąg geometryczny 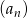 , w którym
, w którym 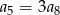 . Wtedy
. Wtedy
A) 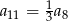 B)
B) 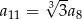 C)
C) 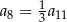 D)
D) 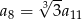
Dany jest nieskończony ciąg geometryczny 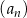 , w którym
, w którym 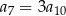 . Wtedy
. Wtedy
A) 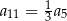 B)
B) 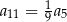 C)
C) 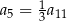 D)
D) 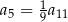
Wszystkie wyrazy nieskończonego ciągu geometrycznego 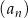 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 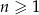 , są dodatnie i
, są dodatnie i 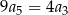 . Wtedy iloraz tego ciągu jest równy
. Wtedy iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 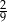 D)
D) 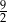
Iloraz nieskończonego ciągu geometrycznego 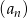 jest równy
jest równy 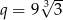 . Wynika stąd, że
. Wynika stąd, że
A) 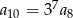 B)
B) 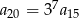 C)
C) 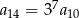 D)
D)