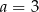Układ liczb 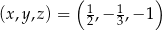 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
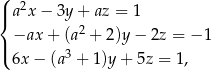
dla
A) 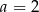 B)
B) 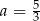 C)
C) 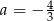 D)
D) 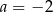
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Układ liczb 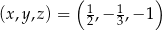 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
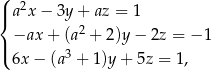
dla
A) 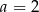 B)
B) 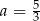 C)
C) 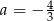 D)
D) 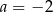
Układ równań 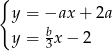 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 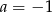 i
i 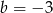 B)
B) 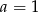 i
i 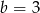 C)
C) 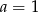 i
i 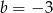 D)
D) 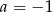 i
i 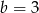
Układ równań 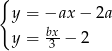 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 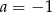 i
i 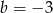 B)
B) 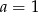 i
i 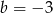 C)
C) 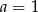 i
i 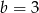 D)
D) 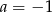 i
i 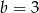
Układ równań 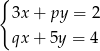 z niewiadomymi
z niewiadomymi  i
i 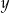 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 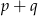 jest równa
jest równa
A) 6 B) 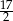 C)
C) 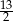 D) 15
D) 15
Układ równań 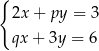 z niewiadomymi
z niewiadomymi  i
i 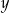 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 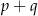 jest równa
jest równa
A) 6 B) 1 C) 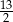 D)
D) 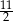
Rozwiązaniem układu równań 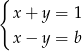 z niewiadomymi
z niewiadomymi  i
i 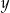 jest para liczb dodatnich. Wynika stąd, że
jest para liczb dodatnich. Wynika stąd, że
A) 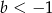 B)
B) 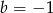 C)
C) 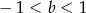 D)
D) 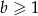
Rozwiązaniem układu równań 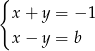 z niewiadomymi
z niewiadomymi  i
i 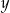 jest para liczb ujemnych. Wynika stąd, że
jest para liczb ujemnych. Wynika stąd, że
A) 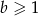 B)
B) 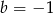 C)
C) 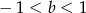 D)
D) 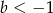
Para liczb 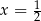 i
i 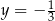 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 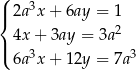 dla
dla
A) 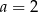 B)
B) 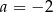 C)
C) 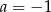 D)
D) 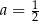
Układ równań 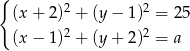 z niewiadomymi
z niewiadomymi 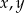 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 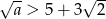 B)
B) 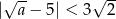 C)
C) 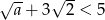 D)
D) 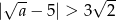
Układ równań 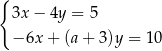 jest sprzeczny dla
jest sprzeczny dla
A) 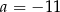 B)
B) 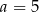 C)
C) 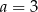 D)
D) 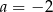
Układ równań 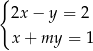 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 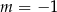 B)
B) 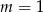 C)
C) 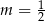 D)
D) 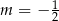
Układ równań 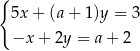 jest sprzeczny dla
jest sprzeczny dla  równego
równego
A) 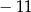 B) 9 C) 4 D)
B) 9 C) 4 D) 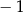
Układ równań 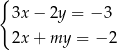 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 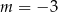 B)
B) 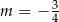 C)
C) 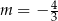 D)
D) 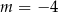
Układ równań 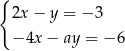 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 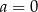 B)
B) 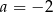 C)
C) 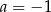 D)
D) 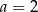
Układ równań 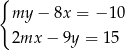 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 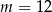 B)
B) 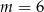 C)
C) 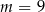 D)
D) 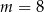
Układ równań 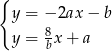 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 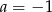 i
i 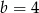 B)
B) 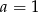 i
i 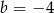 C)
C) 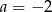 i
i 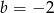 D)
D) 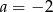 i
i 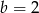
Rozwiązaniem układu równań 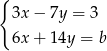 z niewiadomymi
z niewiadomymi  i
i 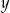 jest para liczb, których suma jest równa 0. Wynika stąd, że
jest para liczb, których suma jest równa 0. Wynika stąd, że
A) 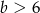 B)
B) 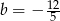 C)
C) 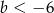 D)
D) 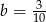
Układ równań 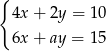 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 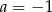 B)
B) 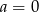 C)
C) 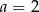 D)
D) 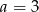
Układ równań 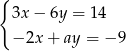 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 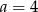 B)
B) 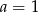 C)
C) 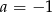 D)
D) 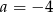
Układ równań 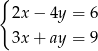 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 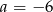 B)
B) 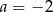 C)
C) 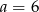 D)
D) 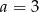
Układ równań 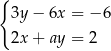 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 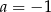 B)
B) 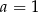 C)
C) 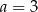 D)
D) 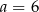
Układ równań 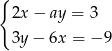 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 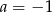 B)
B) 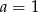 C)
C) 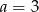 D)
D) 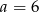
Para liczb 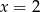 i
i 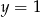 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 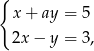 gdy
gdy
A) 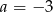 B)
B) 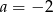 C)
C) 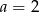 D)
D) 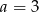
Para liczb 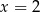 i
i 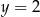 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 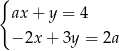 dla
dla
A) 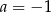 B)
B) 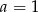 C)
C) 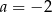 D)
D) 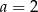
Para liczb 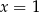 ,
, 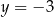 spełnia układ równań
spełnia układ równań
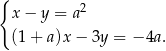
Wtedy  jest równe
jest równe
A) 2 B) 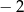 C)
C) 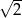 D)
D) 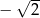
Para liczb 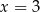 i
i 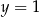 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 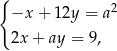 dla
dla
A) 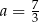 B)
B) 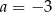 C)
C) 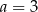 D)
D) 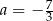
Para liczb 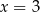 ,
, 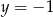 spełnia układ równań
spełnia układ równań
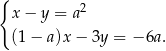
Wtedy  jest równe
jest równe
A) 2 B) 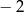 C)
C) 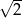 D)
D) 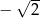
Para liczb 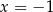 i
i 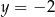 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 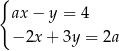 dla
dla
A) 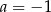 B)
B) 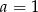 C)
C) 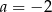 D)
D) 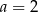
Para liczb 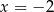 i
i 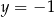 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 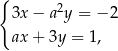 dla
dla
A) 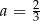 B)
B) 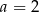 C)
C) 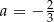 D)
D) 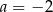
Para liczb 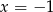 i
i 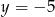 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 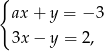 gdy
gdy
A) 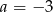 B)
B) 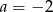 C)
C) 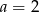 D)
D) 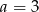
Interpretacją geometryczną układu równań 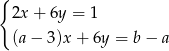 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 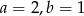 B)
B) 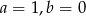 C)
C) 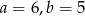 D)
D) 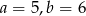
Interpretacją geometryczną układu równań 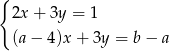 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 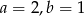 B)
B) 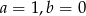 C)
C) 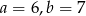 D)
D) 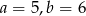
Interpretacją geometryczną układu równań 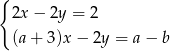 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 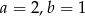 B)
B) 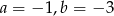 C)
C) 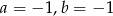 D)
D) 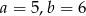
Trójka liczb 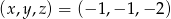 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 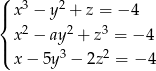 gdy
gdy
A) 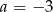 B)
B) 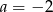 C)
C) 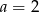 D)
D) 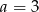
Trójka liczb 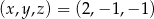 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 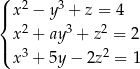 gdy
gdy
A) 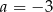 B)
B) 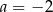 C)
C) 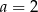 D)
D)