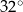W kwadracie 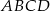 narysowano dwa półokręgi o średnicach
narysowano dwa półokręgi o średnicach 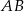 i
i 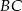 (patrz rysunek).
(patrz rysunek).
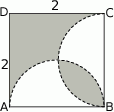
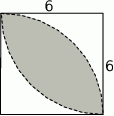
Pole zacieniowanego obszaru jest równe
A) 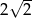 B)
B) 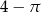 C) 1 D) 2
C) 1 D) 2
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W kwadracie  narysowano dwa półokręgi o średnicach
narysowano dwa półokręgi o średnicach 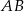 i
i 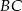 (patrz rysunek).
(patrz rysunek).

Pole zacieniowanego obszaru jest równe
A) 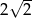 B)
B) 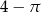 C) 1 D) 2
C) 1 D) 2
Liczba 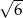 nie jest równa
nie jest równa
A) wysokości trójkąta równobocznego o boku długości 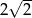
B) długości przekątnej kwadratu o boku długości 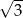
C) polu trójkąta równobocznego o boku długości 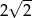
D) polu kwadratu o boku długości 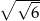
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych elementów i podano długości dwóch fragmentów tego wzoru.
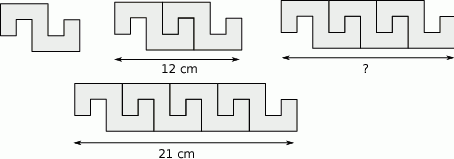
Fragment wzoru złożony z 3 elementów ma długość
A) 15 cm B) 15,75 cm C) 16,5 cm D) 18 cm
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych elementów i podano długości dwóch fragmentów tego wzoru.
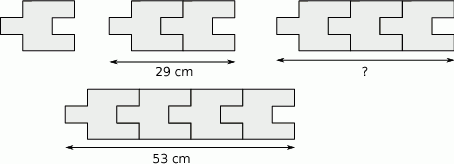
Fragment wzoru złożony z 3 elementów ma długość
A) 41 cm B) 42 cm C) 45 cm D) 48 cm
Na rysunku przedstawiono sposób ułożenia wzoru z jednakowych równoległoboków i trapezów równoramiennych oraz podano długości trzech fragmentów tego wzoru.

Fragment wzoru oznaczony na rysunku znakiem zapytania ma długość
A) 42 cm B) 36 cm C) 54 cm D) 38 cm
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 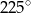 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa 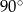 . . | P | F |
| Jeden z dwóch kątów przyległych jest trzy razy większy od drugiego kąta. | P | F |
Dwie przecinające się proste utworzyły cztery kąty. Suma miar trzech z tych kątów jest równa 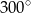 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma miar kątów ostrych wyznaczonych przez te proste jest równa  . . | P | F |
| Jeden z dwóch kątów przyległych jest dwa razy większy od drugiego kąta. | P | F |
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie dwóch kwadratów jednostkowych z kwadratu o boku długości 6, a figura II powstała przez usunięcie dwóch kwadratów jednostkowych z prostokąta o bokach długości 4 i 8.
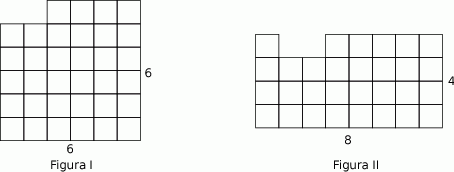
Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Obwód figury I jest równy obwodowi kwadratu o boku 6. | P | F |
| Obwód figury II jest większy od obwodu figury I. | P | F |
Na rysunku przedstawiono dwie figury. Figura I powstała przez usunięcie trzech kwadratów jednostkowych z kwadratu o boku długości 5, a figura II powstała przez usunięcie czterech kwadratów jednostkowych z prostokąta o bokach długości 3 i 7.
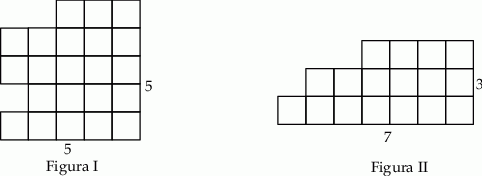
Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Obwód figury I jest równy obwodowi figury II. | P | F |
| Obwód figury II jest równy obwodowi kwadratu o boku 5. | P | F |
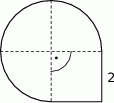
W kwadracie o boku 6 narysowano dwie ćwiartki okręgu o promieniu 6 (patrz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole zacieniowanej figury jest równe 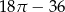 | P | F |
| Obwód zacieniowanej figury jest mniejszy od 21. | P | F |
Narysowana poniżej figura składa się z kwadratu o boku 2 i trzech ćwiartek koła.
Obwód tej figury jest równy
A) 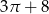 B)
B) 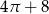 C)
C) 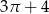 D)
D) 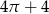
Narysowana poniżej figura składa się z dwóch kwadratów o boku 2 i dwóch ćwiartek koła.
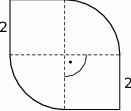
Obwód tej figury jest równy
A) 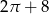 B)
B) 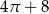 C)
C) 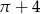 D)
D) 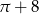
Z kartki w kształcie kwadratu o boku 6 odcięto ćwierć koła o promieniu 6 (patrz rysunek).
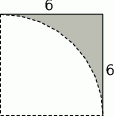
Pole powierzchni pozostałej zacieniowanej części kartki jest równe
A) 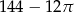 B)
B) 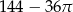 C)
C) 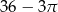 D)
D) 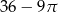
Na rysunku przedstawiono trzy figury: prostokąt, kwadrat, trójkąt.
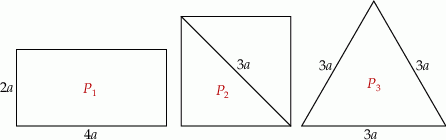
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Spośród przedstawionych figur największe pole ma figura 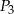 . . | P | F |
Spośród podanych figur najmniejsze pole ma figura  . . | P | F |
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 2 i 1 oraz kąt prosty o wierzchołku  .
.
Następnie od wierzchołka 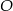 kąta prostego odmierzyła na jednym ramieniu kąta odcinek
kąta prostego odmierzyła na jednym ramieniu kąta odcinek 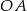 o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek
o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek 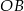 o długości równej przekątnej prostokąta. Długość odcinka
o długości równej przekątnej prostokąta. Długość odcinka 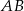 jest równa
jest równa
A) 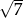 B)
B) 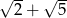 C)
C) 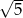 D)
D) 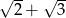
Ewa narysowała kwadrat o boku 1, prostokąt o bokach 3 i 1 oraz kąt prosty o wierzchołku  .
.
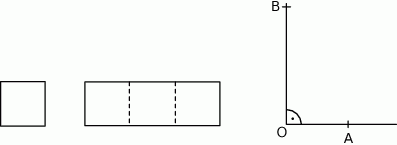
Następnie od wierzchołka  kąta prostego odmierzyła na jednym ramieniu kąta odcinek
kąta prostego odmierzyła na jednym ramieniu kąta odcinek  o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek
o długości równej przekątnej kwadratu, a na drugim ramieniu – odcinek  o długości równej przekątnej prostokąta. Długość odcinka
o długości równej przekątnej prostokąta. Długość odcinka  jest równa
jest równa
A) 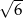 B)
B) 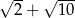 C)
C) 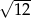 D)
D) 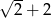
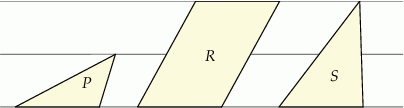
W zeszycie w linie narysowano dwa równoległoboki i trójkąt w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole równoległoboku  jest równe 4.
jest równe 4.
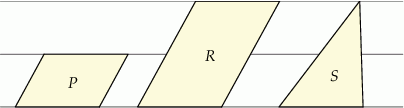
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku  jest równe 8. jest równe 8. | P | F |
Pole trójkąta  jest równe 4. jest równe 4. | P | F |
W zeszycie w linie narysowano dwa trójkąty i równoległobok w sposób pokazany na rysunku. Odległości między sąsiednimi liniami są jednakowe. Podstawy wszystkich tych figur mają taką samą długość. Pole trójkąta  jest równe 4.
jest równe 4.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku  jest równe 12. jest równe 12. | P | F |
Pole trójkąta 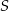 jest równe 8. jest równe 8. | P | F |
Na rysunku przedstawiono sześciokąt foremny o boku równym 2 cm. Przekątna 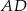 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
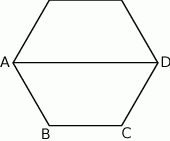
Wysokość trapezu 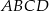 jest równa
jest równa
A) 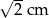 B)
B) 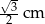 C)
C) 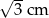 D) 2 cm
D) 2 cm
Na rysunku przedstawiono sześciokąt foremny o boku równym 4 cm. Przekątna 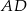 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
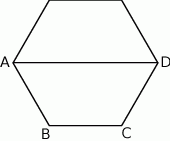
Pole trapezu 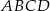 jest równe
jest równe
A) 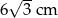 B)
B) 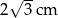 C)
C) 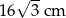 D)
D) 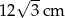
Na rysunku przedstawiono sześciokąt foremny  o boku równym 1 cm.
o boku równym 1 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przekątna 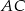 ma długość ma długość 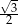 . . | P | F |
Przekątna 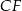 ma długość ma długość 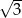 . . | P | F |
Łukasz wyciął z kartki papieru trójkąt równoramienny 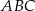 , a następnie zagiął w nim dwa narożniki tak, że wierzchołki
, a następnie zagiął w nim dwa narożniki tak, że wierzchołki  i
i  trójkąta znalazły się w środku
trójkąta znalazły się w środku  jego podstawy. Powstał w ten sposób pięciokąt
jego podstawy. Powstał w ten sposób pięciokąt  .
.
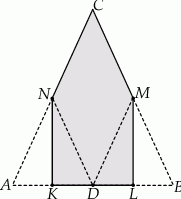
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole pięciokąta  stanowi 75% pola trójkąta stanowi 75% pola trójkąta  . . | P | F |
Obwód pięciokąta 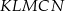 jest taki sam jak obwód trójkąta jest taki sam jak obwód trójkąta 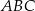 . . | P | F |
Trójkąt równoboczny rozcięto na 16 przystających trójkątów (rysunek I). Z otrzymanych trójkątów ułożono dwa sześciokąty i mniejszy trójkąt równoboczny (rysunek II).
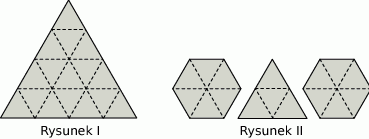
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód dużego trójkąta z rysunku I jest równy sumie obwodów figur na rysunku II. | P | F |
| Suma pól sześciokątów z rysunku II stanowi 75% pola dużego trójkąta z rysunku I. | P | F |
Z kwadratu odcięto trójkąty tak, że linie cięcia przeprowadzono przez środki boków tego kwadratu (rysunek I). Z odciętych trójkątów ułożono trójkąt  (rysunek II).
(rysunek II).
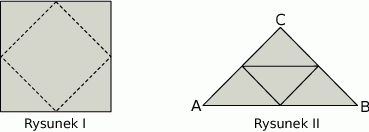
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt  jest prostokątny i równoramienny. jest prostokątny i równoramienny. | P | F |
Pole trójkąta  jest połową pola kwadratu. jest połową pola kwadratu. | P | F |
Suma kątów wewnętrznych pięciokąta foremnego jest równa
A)  B)
B) 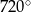 C)
C) 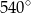 D)
D) 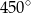
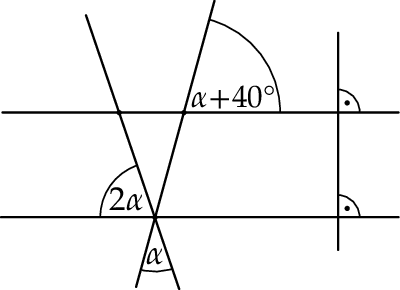
Na rysunku przedstawiono proste 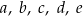 oraz zaznaczono miary niektórych kątów. Proste
oraz zaznaczono miary niektórych kątów. Proste 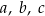 są wzajemnie równoległe. Proste
są wzajemnie równoległe. Proste 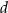 i
i  są wzajemnie prostopadłe i przecinają się w punkcie
są wzajemnie prostopadłe i przecinają się w punkcie 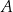 leżącym na prostej
leżącym na prostej 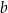 .
.
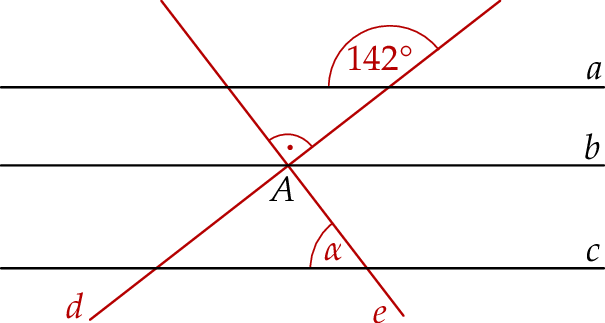
Miara kąta  jest równa
jest równa
A) 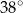 B)
B) 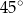 C)
C) 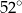 D)
D) 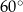
Ponumeruj poniższe czynności od 1 do 4 według kolejności prowadzącej do skonstruowania symetralnej odcinka 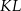 .
.
. . . . . Kreślimy okręgi o promieniu  i środkach w
i środkach w 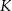 i
i 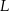 .
.
. . . . . Prowadzimy prostą przechodzącą przez punkty wspólne okręgów.
. . . . . Wybieramy odcinek  większy od połowy długości odcinka
większy od połowy długości odcinka 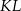 .
.
. . . . . Wyznaczamy punkty wspólne okręgów.
Narysowana poniżej figura składa się z kwadratu i trzech ćwiartek kół.
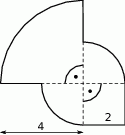
Pole tej figury jest równe
A) 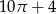 B)
B) 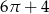 C)
C) 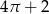 D)
D) 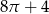
Brzeg narysowanej figury składa się 5 półokręgów.

Pole tej figury jest równe
A) 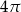 B)
B) 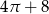 C)
C) 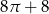 D)
D) 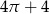
Narysowana poniżej figura składa się z kwadratu i trzech ćwiartek kół.
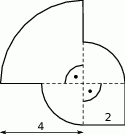
Obwód tej figury jest równy
A) 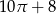 B)
B) 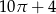 C)
C) 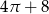 D)
D) 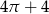
Na przeciwprostokątnej trójkąta prostokątnego o przyprostokątnych długości 1 i 3 zbudowano prostokąt o jednym boku długości 1.
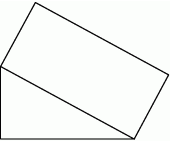
Długość przekątnej tego prostokąta jest równa
A) 3 B) 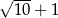 C)
C) 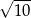 D)
D) 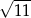
Piotrek na dużej kartce w kratkę narysował figurę złożoną z 60 połączonych odcinków, które kolejno ponumerował liczbami naturalnymi od 1 do 60. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z 17 początkowych odcinków. Kolejne odcinki tej figury Piotrek narysował według tej samej reguły, którą zastosował do narysowania odcinków 1–17.
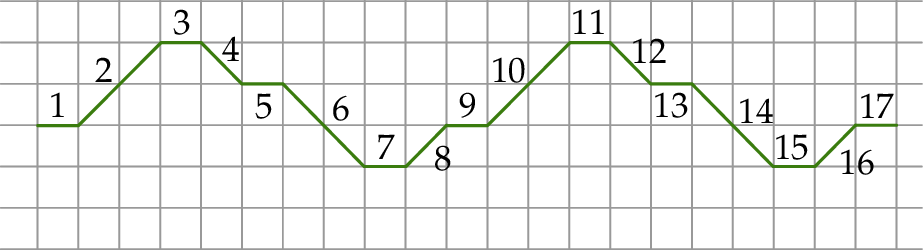
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 39 oraz 53 są wzajemnie równoległe. | P | F |
| Proste zawierające odcinki o numerach 27 oraz 49 są wzajemnie prostopadłe. | P | F |
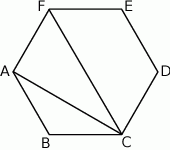
W sześciokącie 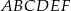 poprowadzono trzy przekątne wychodzące z wierzchołka
poprowadzono trzy przekątne wychodzące z wierzchołka 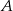 i utworzone przez nie kąty spełniają warunki:
i utworzone przez nie kąty spełniają warunki: 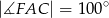 ,
, 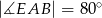 ,
, 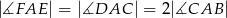 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
 | P | F |
 | P | F |
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 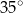 B)
B) 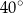 C)
C) 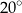 D)
D)