Dla jakich wartości parametru 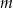 równanie
równanie 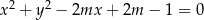 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
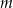 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 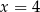 ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich wartości parametru 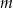 równanie
równanie 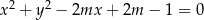 opisuje okrąg?
opisuje okrąg?
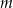 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 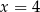 ?
?Znajdź równanie okręgu stycznego do prostej 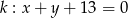 i do prostej
i do prostej 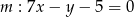 w punkcie
w punkcie 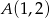 .
.
Napisz równanie okręgu stycznego do osi 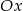 układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej
układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej 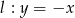 i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do
i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do 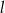 .
.
Okrąg o środku 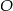 jest wpisany w trójkąt
jest wpisany w trójkąt 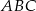 , gdzie
, gdzie 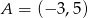 . Wiedząc, że okrąg ten jest styczny do boków
. Wiedząc, że okrąg ten jest styczny do boków 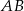 i
i 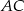 odpowiednio w punktach
odpowiednio w punktach 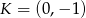 i
i 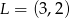 oblicz długość odcinka
oblicz długość odcinka 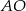 .
.
Wyznacz równanie okręgu przechodzącego przez punkt 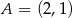 i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Napisz równanie okręgu o środku w punkcie 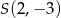 , stycznego do osi
, stycznego do osi 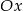 .
.
Środek okręgu, stycznego do osi 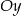 i do prostej o równaniu
i do prostej o równaniu 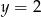 , ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
, ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
Napisz równanie okręgu o promieniu 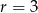 , stycznego do obu osi układu.
, stycznego do obu osi układu.
Prosta o równaniu 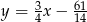 jest styczna od okręgu o środku
jest styczna od okręgu o środku 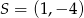 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Prosta o równaniu 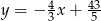 jest styczna od okręgu o środku
jest styczna od okręgu o środku 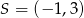 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Wyznacz środek okręgu wpisanego w trójkąt, którego boki zwierają się w prostych o równaniach 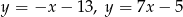 oraz
oraz 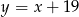 .
.
Napisz równanie okręgu przechodzącego przez punkt 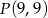 i stycznego do osi
i stycznego do osi  w punkcie
w punkcie 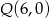 .
.
Do okręgu należy punkt 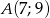 , oraz jest on styczny do osi
, oraz jest on styczny do osi 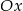 w punkcie
w punkcie 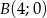 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Punkt 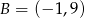 należy do okręgu stycznego do osi
należy do okręgu stycznego do osi 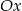 w punkcie
w punkcie 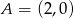 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Do okręgu należy punkt 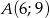 , oraz jest on styczny do osi
, oraz jest on styczny do osi 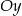 w punkcie
w punkcie 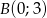 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Napisz równanie okręgu przechodzącego przez punkt 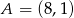 i stycznego do osi
i stycznego do osi 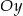 w punkcie
w punkcie 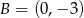 .
.
Wyznacz równanie okręgu o środku 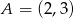 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 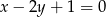 .
.
Wyznacz równanie okręgu o środku 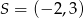 stycznego do prostej
stycznego do prostej 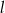 o równaniu
o równaniu 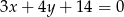 .
.
Wyznacz równanie okręgu o środku 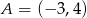 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 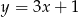 .
.
Znajdź równanie okręgu o środku w punkcie 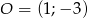 , wiedząc, że okrąg jest styczny do prostej
, wiedząc, że okrąg jest styczny do prostej 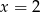 .
.
Dany jest okrąg o środku w punkcie 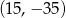 i promieniu 16. Sprawdź czy okrąg ten jest styczny do
i promieniu 16. Sprawdź czy okrąg ten jest styczny do
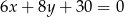 ,
, 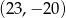 i promieniu 2?
i promieniu 2?Uzasadnij swoją odpowiedź.
Znajdź równanie okręgu przechodzącego przez punkt 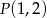 i stycznego jednocześnie do prostych
i stycznego jednocześnie do prostych 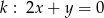 i
i 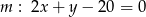 .
.
Napisz równanie okręgu stycznego do osi 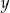 w punkcie
w punkcie 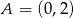 i przechodzącego przez punkt
i przechodzącego przez punkt 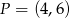 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 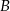 i
i 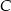 , aby trójkąt
, aby trójkąt 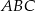 był równoboczny.
był równoboczny.
Okrąg  ma środek
ma środek 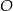 i jest styczny prostej
i jest styczny prostej 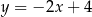 w punkcie
w punkcie 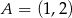 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu  , jeżeli
, jeżeli ![−→ OA = [2,1]](https://img.zadania.info/zad/7820974/HzadT5x.gif) .
.
Okrąg jest styczny do osi układu współrzędnych w punktach 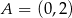 i
i 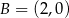 oraz jest styczny do prostej
oraz jest styczny do prostej 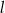 w punkcie
w punkcie 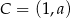 , gdzie
, gdzie 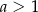 . Wyznacz równanie prostej
. Wyznacz równanie prostej 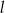 .
.
Okrąg jest styczny do osi układu współrzędnych w punktach 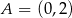 i
i 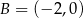 oraz jest styczny do prostej
oraz jest styczny do prostej 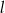 w punkcie
w punkcie 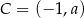 , gdzie
, gdzie 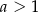 . Wyznacz równanie prostej
. Wyznacz równanie prostej 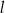 .
.
Wyznacz równanie okręgu stycznego do osi 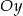 , którego środkiem jest punkt
, którego środkiem jest punkt 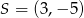 .
.
Okrąg o środku w punkcie 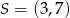 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 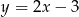 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 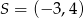 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 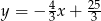 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 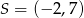 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 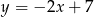 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 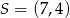 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 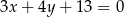 . Oblicz promień tego okręgu oraz współrzędne punktu styczności.
. Oblicz promień tego okręgu oraz współrzędne punktu styczności.
Napisz równanie okręgu, który jest styczny do prostej 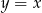 w punkcie
w punkcie 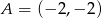 , oraz który odcina z prostej
, oraz który odcina z prostej 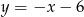 cięciwę o długości 8.
cięciwę o długości 8.
Z punktu 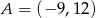 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 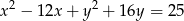 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Z punktu 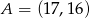 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 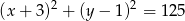 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
