Wartość wyrażenia 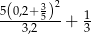 wynosi
wynosi
A)  B)
B)  C)
C) 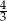 D)
D) 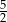
/Szkoła średnia/Zadania testowe/Liczby/Liczby wymierne
Wartość wyrażenia 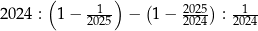 jest równa
jest równa
A) 0 B) 1 C) 2024 D) 2026
Iloraz liczb 5670 i 6615 jest równy
A) 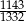 B)
B) 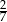 C)
C)  D)
D) 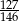
Iloraz liczb 2016 i 4704 jest równy
A) 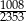 B)
B) 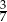 C)
C)  D)
D) 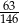
Liczbą wymierną nie jest liczba
A) 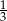 B)
B) 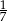 C)
C) 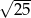 D)
D) 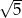
Liczbą wymierną nie jest liczba
A) 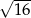 B)
B) 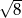 C)
C) 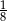 D)
D) 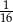
Liczbą wymierną nie jest liczba
A) 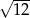 B)
B) 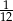 C)
C) 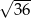 D)
D) 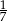
Ile liczb wymiernych znajduje się w zbiorze
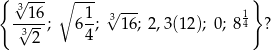
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się wśród liczb

A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się wśród liczb
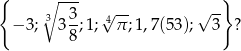
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się wśród liczb
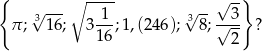
A) 2 B) 3 C) 4 D) 5
Ile liczb wymiernych znajduje się w zbiorze
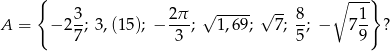
A) 3 B) 4 C) 5 D) 6
Różnica 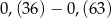 jest równa
jest równa
A) 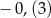 B)
B) 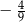 C)
C) 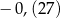 D)
D) 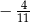
Suma dwóch liczb niewymiernych
A) może być liczbą całkowitą B) nie może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) nie może być liczbą wymierną
Które z poniższych zdań jest prawdziwe?
A) Liczba przeciwna do liczby wymiernej jest liczbą niewymierną
B) Liczba 1 jest jednocześnie liczbą wymierną i niewymierną
C) Odwrotność każdej liczby całkowitej jest liczbą całkowitą
D) Liczba 0 jest liczbą wymierną
Różnica dwóch liczb niewymiernych
A) nie może być liczbą wymierną B) nie może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) może być liczbą całkowitą
Iloczyn dwóch liczb niewymiernych
A) nie może być liczbą całkowitą B) może być liczbą całkowitą
C) jest zawsze liczbą niewymierną D) nie może być liczbą wymierną
Rozwinięcie dziesiętne nieskończone ma liczba
A) 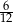 B)
B) 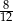 C)
C) 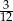 D)
D) 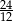
Rozwinięcie dziesiętne nieskończone ma liczba
A) 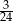 B)
B) 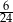 C)
C) 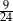 D)
D) 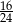
Rozwinięcie dziesiętne nieskończone ma liczba
A) 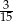 B)
B) 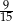 C)
C) 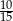 D)
D) 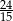
Różnica 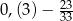 jest równa
jest równa
A) 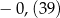 B)
B) 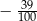 C)
C) 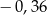 D)
D) 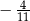
Różnica 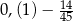 jest równa
jest równa
A) 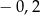 B)
B) 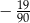 C)
C) 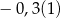 D)
D) 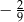
Do przedziału 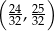 należy liczba
należy liczba
A) 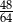 B)
B) 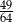 C)
C) 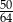 D)
D) 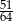
Do przedziału 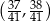 należy liczba
należy liczba
A) 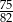 B)
B) 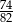 C)
C) 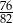 D)
D) 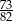
Do przedziału 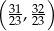 należy liczba
należy liczba
A) 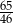 B)
B)  C)
C) 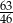 D)
D) 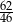
Wielkości  i
i 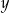 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 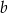 | 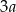 |  |
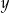 | 48 | 8 |  | 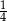 |
Stąd wynika, że
A) 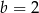 B)
B) 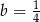 C)
C) 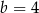 D)
D) 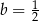
Liczbę 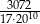 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Piętnastą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Piętnastą cyfrą po przecinku jego rozwinięcia jest
A) 6 B) 4 C) 7 D) 0
Liczbą wymierną jest liczba
A) 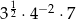 B)
B) 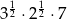 C)
C) 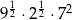 D)
D) 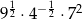
Liczbą wymierną jest liczba
A) 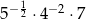 B)
B) 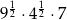 C)
C) 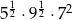 D)
D) 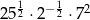
Liczbą niewymierną jest liczba
A) 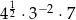 B)
B) 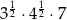 C)
C) 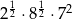 D)
D) 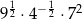
W zbiorze 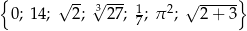
A) jest dokładnie 1 liczba wymierna B) są dokładnie 2 liczby wymierne
C) są dokładnie 3 liczby wymierne D) są dokładnie 4 liczby wymierne
W zbiorze 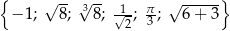
A) jest dokładnie 1 liczba wymierna B) są dokładnie 2 liczby wymierne
C) są dokładnie 3 liczby wymierne D) są dokładnie 4 liczby wymierne
W zbiorze 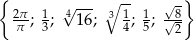
A) są dokładnie 2 liczby wymierne B) są dokładnie 3 liczby wymierne
C) są dokładnie 4 liczby wymierne D) jest dokładnie 5 liczb wymiernych
Dany jest zbiór 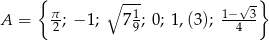 . Liczb wymiernych w zbiorze
. Liczb wymiernych w zbiorze 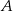 jest
jest
A) pięć B) dwie C) trzy D) cztery
Liczbą wymierną nie jest:
A) 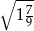 B)
B) 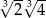 C)
C) 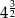 D)
D) 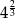
Do zbioru liczb wymiernych nie należy liczba
A) 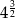 B)
B) 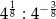 C)
C) 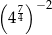 D)
D) 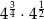
Liczbą wymierną jest:
A) 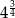 B)
B) 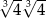 C)
C) 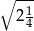 D)
D) 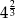
Rozwinięcie dziesiętne skończone ma liczba:
A) 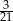 B)
B) 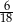 C)
C) 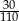 D)
D) 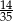
Wielkości  i
i 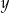 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 3 | 8 |
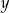 | 36 | 24 | 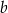 |
Stąd wynika, że
A) 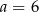 ,
, 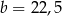 B)
B) 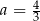 ,
, 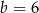 C)
C) 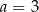 ,
, 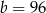 D)
D) 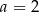 ,
, 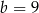
Wielkości  i
i 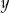 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 | 3 |  | 2 |
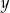 | 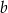 | 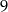 | 36 |
Stąd wynika, że
A) 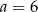 ,
, 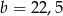 B)
B) 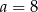 ,
, 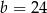 C)
C) 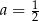 ,
, 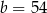 D)
D) 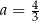 ,
, 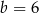
Dany jest zbiór 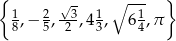 . Ile liczb należących do zbioru
. Ile liczb należących do zbioru 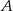 ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
A) 2 B) 3 C) 4 D) 5
Dany jest zbiór 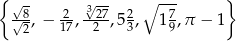 . Ile liczb należących do zbioru
. Ile liczb należących do zbioru 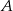 ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
A) 5 B) 4 C) 3 D) 2
W rozwinięciu dziesiętnym ułamka 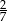 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 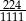 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 6
W rozwinięciu dziesiętnym ułamka 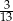 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 6 B) 9 C) 2 D) 3
W rozwinięciu dziesiętnym ułamka 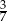 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 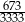 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 9
W rozwinięciu dziesiętnym ułamka 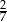 na czterdziestym miejscu po przecinku stoi cyfra
na czterdziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 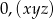 . Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 732 B) 273 C) 244 D) 723
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 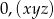 . Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka  jest więc równy
jest więc równy
A) 79 B) 273 C) 237 D) 244
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 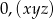 . Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 372 B) 273 C) 244 D) 124

