Zbiór liczb, które na osi liczbowej są równoodległe od liczb 4 i 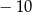 , można opisać za pomocą równania
, można opisać za pomocą równania
A) 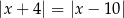 B)
B) 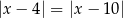
C) 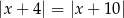 D)
D) 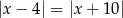
/Szkoła średnia/Zadania testowe/Równania/Z wartością bezwzględną
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 5 i 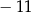 , można opisać za pomocą równania
, można opisać za pomocą równania
A) 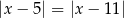 B)
B) 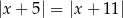
C) 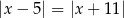 D)
D) 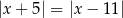
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 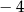 i 10, można opisać za pomocą równania
i 10, można opisać za pomocą równania
A) 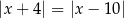 B)
B) 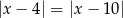
C) 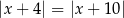 D)
D) 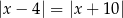
Liczba 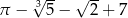 jest rozwiązaniem równania
jest rozwiązaniem równania 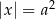 z niewiadomą
z niewiadomą  . Która z podanych liczb jest również rozwiązaniem tego równania?
. Która z podanych liczb jest również rozwiązaniem tego równania?
A) 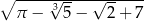 B)
B) 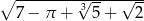
C) 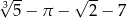 D)
D) 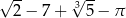
Zbiorem wszystkich rozwiązań równania 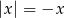 jest
jest
A) 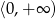 B)
B) 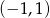 C)
C) 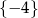 D)
D) 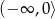
Zbiorem wszystkich rozwiązań równania 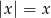 jest
jest
A) 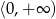 B)
B) 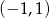 C)
C) 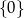 D)
D) 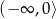
Równanie 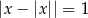 ? ma
? ma
A) nieskończenie wiele rozwiązań. B) jedno rozwiązanie.
C) dwa rozwiązania. D) zero rozwiązań.
Ile rozwiązań ma równanie 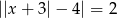 ?
?
A) 0 B) 2 C) 4 D) 6
Ile rozwiązań ma równanie 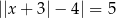 ?
?
A) 0 B) 2 C) 4 D) 6
Ile rozwiązań ma równanie 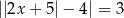 ?
?
A) 0 B) 1 C) 2 D) 4
Równanie 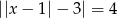 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Ile rozwiązań ma równanie 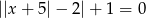 ?
?
A) 0 B) 2 C) 4 D) 6
Równanie 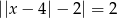 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Rozwiązaniem równania 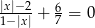 są liczby
są liczby
A) 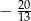 i
i 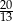 B)
B) 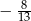 i
i 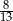 C) -8 i 8 D) -20 i 20
C) -8 i 8 D) -20 i 20
Zbiór liczb, których odległości na osi liczbowej od liczby -9 jest równa 5, można opisać równaniem
A) 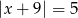 B)
B) 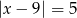 C)
C) 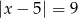 D)
D) 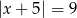
Zbiór liczb, których odległości na osi liczbowej od liczby -7 jest równa 9, można opisać równaniem
A) 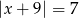 B)
B) 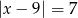 C)
C) 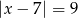 D)
D) 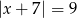
Zbiór liczb, których odległości na osi liczbowej od liczby -5 jest równa 9, można opisać równaniem
A) 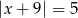 B)
B) 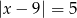 C)
C) 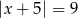 D)
D) 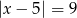
Równanie 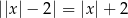
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Równanie 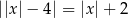
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Liczbami spełniającymi równanie 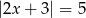 są
są
A) 1 i 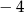 B) 1 i 2 C)
B) 1 i 2 C) 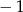 i 4 D)
i 4 D) 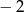 i 2
i 2
Liczbami spełniającymi równanie 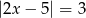 są
są
A) 1 i 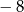 B) 1 i 4 C)
B) 1 i 4 C) 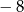 i 4 D)
i 4 D) 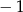 i 4
i 4
Liczbami spełniającymi równanie 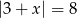 są
są
A) 11 i 5 B) 3 i 8 C) 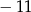 i 5 D)
i 5 D) 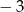 i 8
i 8
Liczba różnych pierwiastków równania 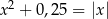 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Dane jest równanie 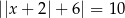 . Iloczyn rozwiązań tego równania jest równy
. Iloczyn rozwiązań tego równania jest równy
A) 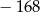 B)
B) 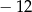 C) 216 D) 3024
C) 216 D) 3024
Wskaż liczbę, która spełnia równanie 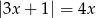 .
.
A) 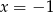 B)
B) 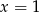 C)
C) 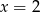 D)
D) 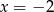
Wskaż liczbę, która spełnia równanie 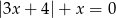 .
.
A) 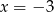 B)
B) 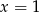 C)
C) 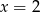 D)
D) 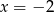
Wskaż liczbę, która spełnia równanie 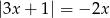 .
.
A) 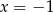 B)
B) 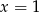 C)
C) 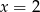 D)
D) 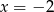
Wskaż liczbę, która spełnia równanie 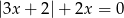 .
.
A) 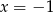 B)
B) 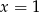 C)
C) 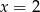 D)
D) 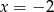
Wskaż 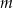 , dla którego rozwiązaniem równania
, dla którego rozwiązaniem równania 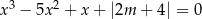 jest liczba 2.
jest liczba 2.
A) 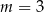 lub
lub 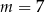 B)
B) 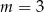 lub
lub 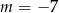
C) 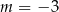 lub
lub 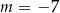 D)
D) 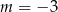 lub
lub 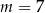
Wskaż liczbę, która spełnia równanie 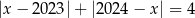 .
.
A) 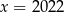 B)
B) 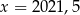 C)
C) 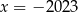 D)
D) 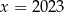
Liczba różnych pierwiastków równania 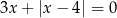 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 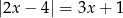 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie cztery rozwiązania.
Liczba różnych pierwiastków równania 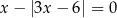 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 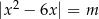 o niewiadomej
o niewiadomej  ma cztery rozwiązania dla
ma cztery rozwiązania dla 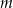
A) 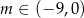 B)
B) 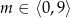 C)
C) 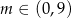 D)
D) 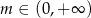
Równanie 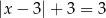 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania
C) nieskończenie wiele rozwiązań D) zero rozwiązań
Równanie 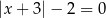
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Równanie 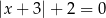
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Równanie 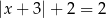
A) jest sprzeczne B) jest tożsamościowe
C) ma jedno rozwiązanie D) ma dwa rozwiązania
Wskaż liczbę, która spełnia równanie 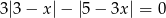
A)  B)
B) 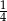 C)
C)  D)
D) 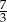
Liczby 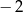 i
i 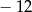 są rozwiązaniami równania
są rozwiązaniami równania
A) 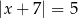 B)
B) 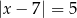 C)
C) 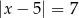 D)
D) 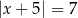
Liczby 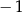 i 9 są rozwiązaniami równania
i 9 są rozwiązaniami równania
A) 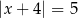 B)
B) 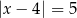 C)
C) 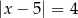 D)
D) 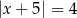
Liczby 2 i 8 są rozwiązaniami równania
A) 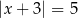 B)
B) 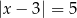 C)
C) 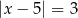 D)
D) 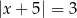
Liczba rozwiązań równania 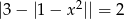 jest równa
jest równa
A) 6 B) 4 C) 2 D) 5

