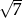Przekątna prostopadłościanu o wymiarach 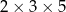 ma długość
ma długość
A) 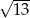 B)
B) 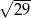 C)
C) 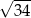 D)
D) 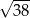
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przekątna prostopadłościanu o wymiarach 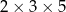 ma długość
ma długość

A) 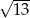 B)
B) 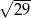 C)
C) 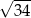 D)
D) 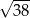
Przekątna prostopadłościanu o wymiarach 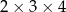 ma długość
ma długość
A) 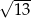 B)
B) 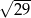 C) 5 D) 6
C) 5 D) 6
Przekątna prostopadłościanu o wymiarach 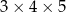 ma długość
ma długość
A) 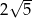 B)
B) 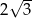 C)
C) 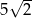 D)
D) 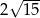
Pudełko w kształcie prostopadłościanu ma wymiary 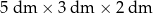 (zobacz rysunek).
(zobacz rysunek).
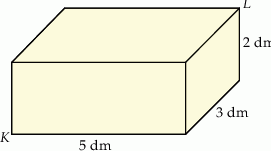
Przekątna  tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 5,83 dm B) 6,16 dm C) 3,61 dm D) 5,39 dm
Bloczek betonowy fundamentowy ma kształt prostopadłościanu o wymiarach 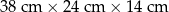 (zobacz rysunek).
(zobacz rysunek).
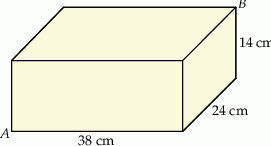
Przekątna 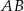 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 4,71 dm B) 4,49 dm C) 4,05 dm D) 4,7 dm
Pudełko w kształcie prostopadłościanu ma wymiary 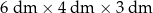 (zobacz rysunek).
(zobacz rysunek).
Przekątna 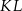 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 6,83 dm B) 6,16 dm C) 7,81 dm D) 5,39 dm
Dane są dwa prostopadłościany podobne: 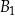 oraz
oraz 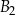 . Objętość prostopadłościanu
. Objętość prostopadłościanu 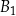 jest równa
jest równa 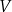 , a objętość prostopadłościanu
, a objętość prostopadłościanu 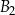 jest równa
jest równa 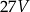 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 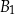 jest równe
jest równe 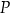 . Pole powierzchni całkowitej prostopadłościanu
. Pole powierzchni całkowitej prostopadłościanu 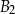 jest równe
jest równe
A) 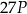 , , | B) 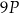 , , | C) 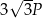 |
ponieważ stosunek pól powierzchni całkowitych prostopadłościanów podobnych jest równy
| 1) | stosunkowi objętości tych prostopadłościanów. |
| 2) | pierwiastkowi kwadratowemu ze stosunku objętości tych prostopadłościanów. |
| 3) | kwadratowi stosunku długości odcinków odpowiadających w obu prostopadłościanach. |
Przekrojem prostopadłościanu zawierającym przekątną podstawy i przekątne sąsiednich ścian bocznych wychodzących z tego samego wierzchołka jest
A) kwadrat B) prostokąt C) trójkąt D) trapez
Długości trzech wychodzących z jednego wierzchołka krawędzi prostopadłościanu są trzema kolejnymi liczbami naturalnymi parzystymi. Najdłuższa krawędź tego prostopadłościanu ma długość 10. Pole powierzchni całkowitej tego prostopadłościanu jest równe
A) 376 B) 466 C) 480 D) 720
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość najmniejszej z utworzonych części?
A) 15% B) 25% C) 17% D) 12,5%
Prostopadłościan dzielimy na części prowadząc dwie płaszczyzny równoległe do jego podstaw, które dzielą krawędź boczną w stosunku 5:1:2. Jaki procent objętości całego prostopadłościanu stanowi objętość największej z utworzonych części?
A) 62,5% B) 37,5% C) 65% D) 75%
Z prostopadłościanu 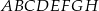 odcięto ostrosłup
odcięto ostrosłup 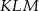 w ten sposób, że punkty
w ten sposób, że punkty 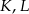 i
i 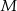 są środkami krawędzi
są środkami krawędzi 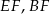 i
i 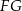 (zobacz rysunek).
(zobacz rysunek).
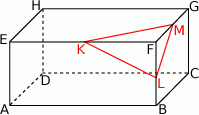
Ile razy objętość odciętego ostrosłupa jest mniejsza od objętości pozostałej części prostopadłościanu?
A) 48 razy. B) 47 razy. C) 46 razy. D) 24 razy.
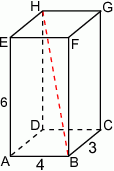
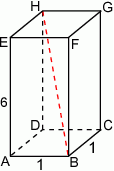
Wymiary prostopadłościanu  podane są na rysunku. Przekątna
podane są na rysunku. Przekątna  prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy  pod kątem
pod kątem  takim, że
takim, że
A) 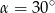 B)
B) 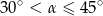 C)
C) 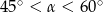 D)
D) 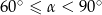
Wymiary prostopadłościanu  podane są na rysunku. Przekątna
podane są na rysunku. Przekątna  prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy  pod kątem
pod kątem  takim, że
takim, że
A) 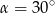 B)
B) 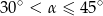 C)
C) 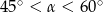 D)
D) 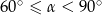
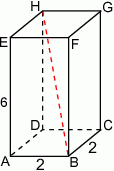
Wymiary prostopadłościanu  podane są na rysunku. Przekątna
podane są na rysunku. Przekątna  prostopadłościanu jest nachylona do płaszczyzny podstawy
prostopadłościanu jest nachylona do płaszczyzny podstawy  pod kątem
pod kątem  takim, że
takim, że
A) 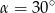 B)
B) 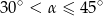 C)
C) 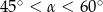 D)
D) 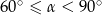
W prostopadłościanie o objętości 3400 skrócono o 10% najkrótsze krawędzie, a następnie wydłużono najdłuższe krawędzie tak, aby otrzymany prostopadłościan miał objętość 3519. O ile procent wydłużono najdłuższe krawędzie prostopadłościanu?
A) 18% B) 12% C) 15% D) 20%
Dany jest prostopadłościan o wymiarach 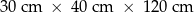 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 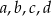 , o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
, o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i  .
.
C) tylko od odcinków 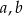 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dany jest prostopadłościan o wymiarach 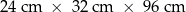 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 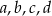 , o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
, o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
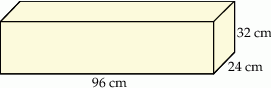
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 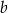 .
.
C) tylko od odcinków 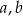 i
i  .
.
D) od wszystkich czterech danych odcinków.
Pole powierzchni całkowitej prostopadłościanu o wymiarach 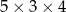 jest równe
jest równe
A) 94 B) 60 C) 47 D) 20
Pole powierzchni całkowitej prostopadłościanu o wymiarach 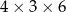 jest równe
jest równe
A) 94 B) 54 C) 108 D) 72
Podstawą prostopadłościanu jest prostokąt o wymiarach 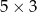 , a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
, a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
A) 2 B) 3 C) 4 D) 5
Długości trzech krawędzi prostopadłościanu, mających wspólny koniec, są kolejnymi liczbami nieparzystymi. Jedna z tych krawędzi ma długość  . Objętość tego prostopadłościanu może być równa:
. Objętość tego prostopadłościanu może być równa:
A) 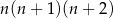 B)
B) 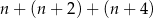
C) 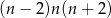 D)
D) 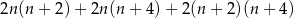
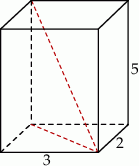
Dany jest prostopadłościan 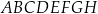 o krawędziach długości
o krawędziach długości 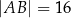 ,
, 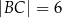 i
i 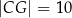 . Wewnątrz tego prostopadłościanu znajduje się punkt
. Wewnątrz tego prostopadłościanu znajduje się punkt  (zobacz rysunek).
(zobacz rysunek).
Suma odległości punktu 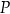 od wszystkich ścian prostopadłościanu
od wszystkich ścian prostopadłościanu  jest równa
jest równa
A) 45 B) 20 C) 25 D) 32
Dany jest prostopadłościan o krawędziach długości  ,
, 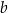 i
i  , gdzie
, gdzie 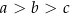 . Suma długości wszystkich krawędzi tego prostopadłościanu jest równa 116. Pole powierzchni całkowitej prostopadłościanu jest równe 552. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Suma długości wszystkich krawędzi tego prostopadłościanu jest równa 116. Pole powierzchni całkowitej prostopadłościanu jest równe 552. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami krawędzi tego prostopadłościanu zapisano w układzie równań
A) 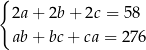 B)
B) 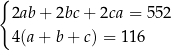 C)
C) 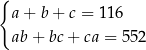
D) 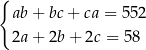 E)
E) 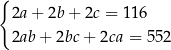 F)
F) 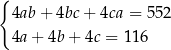
Stosunek długości trzech krawędzi prostopadłościanu o objętości 240 jest równy 2:3:5. Pole powierzchni tego prostopadłościanu jest równe:
A) 124 B) 248 C) 496 D) 62
Dany jest prostopadłościan o wymiarach 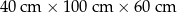 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
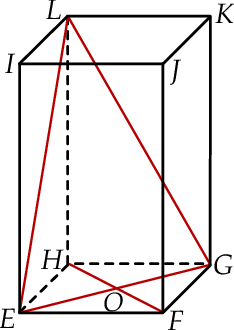
W graniastosłupie prawidłowym czworokątnym  wierzchołki
wierzchołki  połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
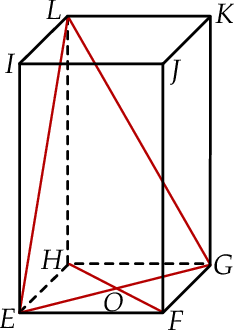
Wskaż kąt między wysokością 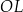 trójkąta
trójkąta 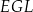 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 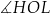 B)
B) 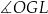 C)
C) 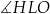 D)
D) 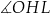
W graniastosłupie prawidłowym czworokątnym  wierzchołki
wierzchołki  połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
Wskaż kąt między wysokością  trójkąta
trójkąta  i krawędzią boczną tego graniastosłupa.
i krawędzią boczną tego graniastosłupa.
A) 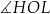 B)
B) 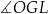 C)
C) 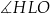 D)
D) 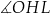
W prostopadłościanie 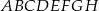 mamy:
mamy: 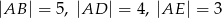 . Który z odcinków
. Który z odcinków 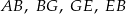 jest najdłuższy?
jest najdłuższy?
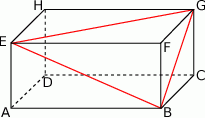
A) 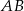 B)
B) 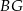 C)
C) 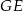 D)
D) 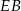
W prostopadłościanie 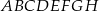 mamy:
mamy: 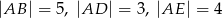 . Który z odcinków
. Który z odcinków 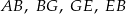 jest najdłuższy?
jest najdłuższy?
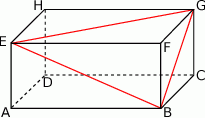
A) 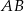 B)
B) 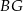 C)
C) 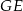 D)
D) 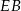
Długość, szerokość i wysokość prostopadłościanu są w stosunku 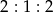 . Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
A) 4 B) 8 C) 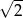 D) 2
D) 2
Długość, szerokość i wysokość prostopadłościanu są w stosunku 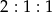 . Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
A) 6 B) 24 C) 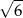 D) 12
D) 12
Długość, szerokość i wysokość prostopadłościanu są w stosunku 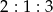 . Przekątna prostopadłościanu ma długość 14. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 14. Pole podstawy prostopadłościanu jest równe
A) 28 B) 14 C) 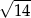 D)
D)