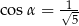Okrąg jest styczny do boku 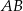 trójkąta
trójkąta 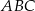 w punkcie
w punkcie 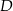 oraz przecina boki
oraz przecina boki 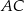 i
i 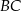 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 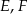 i
i 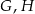 (zobacz rysunek). Kat
(zobacz rysunek). Kat 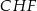 ma miarę
ma miarę 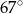 .
.
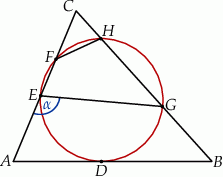
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 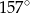 B)
B) 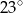 C)
C) 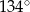 D)
D) 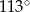
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Okrąg jest styczny do boku 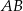 trójkąta
trójkąta 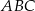 w punkcie
w punkcie 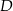 oraz przecina boki
oraz przecina boki 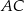 i
i 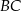 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 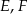 i
i 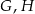 (zobacz rysunek). Kat
(zobacz rysunek). Kat 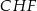 ma miarę
ma miarę 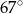 .
.

Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 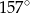 B)
B) 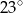 C)
C) 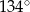 D)
D) 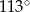
Okrąg jest styczny do boku 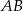 trójkąta
trójkąta 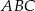 w punkcie
w punkcie 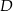 oraz przecina boki
oraz przecina boki 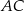 i
i 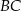 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 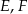 i
i 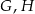 (zobacz rysunek). Kat
(zobacz rysunek). Kat 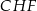 ma miarę
ma miarę 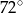 .
.
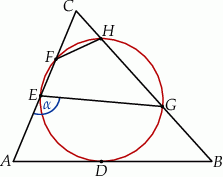
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 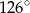 B)
B) 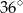 C)
C) 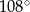 D)
D) 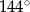
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 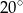 i
i 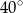 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 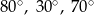 B)
B) 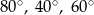 C)
C) 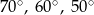 D)
D) 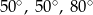
Kąty między bokiem trójkąta ostrokątnego a wysokościami opuszczonymi z należących do tego boku wierzchołków mają miary 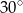 i
i 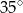 . Kąty tego trójkąta mają miary:
. Kąty tego trójkąta mają miary:
A) 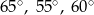 B)
B) 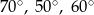 C)
C) 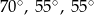 D)
D) 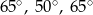
Dany jest trójkąt o bokach długości 4, 5 oraz 6. Cosinus największego kąta wewnętrznego tego trójkąta jest równy
A) 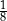 B)
B) 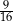 C)
C)  D)
D) 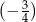
Sinusy dwóch kątów ostrych trójkąta są odpowiednio równe 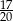 i
i 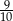 . Jeżeli
. Jeżeli  jest miarą najmniejszego kąta tego trójkąta, to
jest miarą najmniejszego kąta tego trójkąta, to
A) 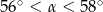 B)
B) 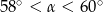 C)
C) 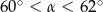 D)
D) 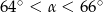
Dany jest trójkąt 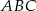 o kącie
o kącie 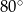 przy wierzchołku
przy wierzchołku 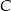 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 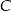 ma miarę
ma miarę 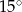 . Wynika stąd, że kąt
. Wynika stąd, że kąt 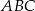 jest równy
jest równy
A) 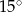 B)
B) 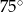 C)
C) 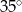 D)
D) 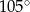
Dany jest trójkąt 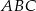 o kącie
o kącie 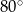 przy wierzchołku
przy wierzchołku 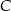 . Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka
. Kąt między dwusieczną tego kąta a wysokością poprowadzoną z wierzchołka 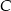 ma miarę
ma miarę 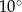 . Wynika stąd, że kąt
. Wynika stąd, że kąt 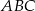 jest równy
jest równy
A) 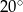 B)
B) 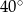 C)
C) 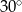 D)
D) 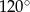
Dany jest trójkąt 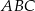 , w którym
, w którym 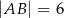 ,
, 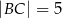 ,
, 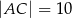 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 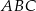 jest równy jest równy 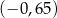 . . | P | F |
Trójkąt 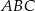 jest rozwartokątny. jest rozwartokątny. | P | F |
Dany jest trójkąt 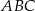 , w którym
, w którym 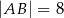 ,
, 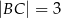 ,
, 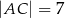 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 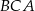 jest równy jest równy 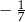 . . | P | F |
Trójkąt 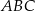 jest ostrokątny. jest ostrokątny. | P | F |
Wierzchołki trójkąta 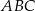 leżą na okręgu i środek
leżą na okręgu i środek 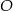 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 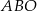 ma miarę
ma miarę 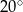 , to kąt
, to kąt 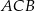 ma miarę
ma miarę
A) 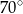 B)
B) 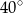 C)
C) 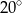 D)
D) 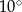
Wierzchołki trójkąta 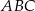 leżą na okręgu i środek
leżą na okręgu i środek 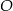 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 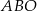 ma miarę
ma miarę 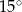 , to kąt
, to kąt 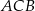 ma miarę
ma miarę
A) 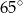 B)
B) 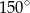 C)
C) 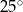 D)
D) 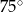
Na trójkącie ostrokątnym 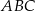 opisano okrąg o środku
opisano okrąg o środku 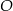 . Miara kąta
. Miara kąta 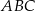 jest równa
jest równa 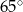 . Miara kąta
. Miara kąta 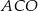 jest równa
jest równa
A) 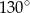 B)
B) 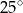 C)
C) 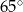 D)
D) 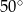
Wierzchołki trójkąta 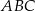 leżą na okręgu i środek
leżą na okręgu i środek 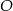 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 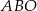 ma miarę
ma miarę 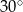 , to kąt
, to kąt 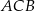 ma miarę
ma miarę
A) 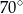 B)
B) 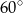 C)
C) 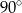 D)
D) 
Wierzchołki trójkąta 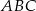 leżą na okręgu o środku
leżą na okręgu o środku 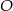 .
. 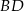 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 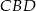 ma miarę
ma miarę 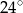 , to kąt
, to kąt 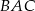 ma miarę
ma miarę
A) 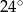 B)
B) 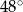 C)
C) 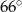 D)
D) 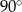
Wierzchołki trójkąta 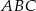 leżą na okręgu o środku
leżą na okręgu o środku 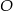 .
. 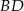 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 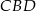 ma miarę
ma miarę 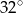 , to kąt
, to kąt 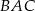 ma miarę
ma miarę
A) 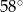 B)
B) 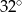 C)
C) 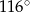 D)
D) 
Wierzchołki trójkąta 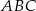 leżą na okręgu o środku
leżą na okręgu o środku 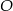 .
. 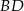 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 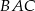 ma miarę
ma miarę 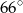 , to kąt
, to kąt 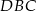 ma miarę
ma miarę
A) 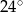 B)
B) 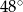 C)
C) 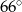 D)
D) 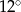
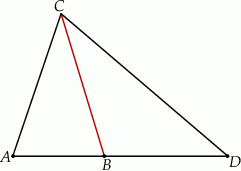
Punkty 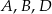 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 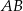 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
Jeżeli 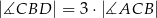 , to
, to 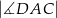 wynosi
wynosi
A) 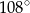 B)
B) 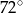 C)
C) 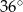 D)
D) 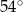
Odcinki 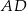 i
i 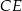 są wysokościami trójkąta
są wysokościami trójkąta 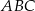 .
.
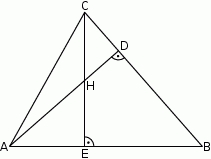
Zatem
A) 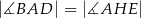 B)
B) 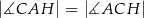
C) 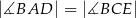 D)
D) 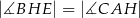
W trójkącie stosunek miar kątów jest równy 3:4:5. Zatem najmniejszy kąt tego trójkąta ma miarę
A) 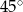 B)
B) 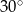 C)
C) 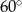 D)
D) 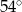
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 3:4:5. Najmniejszy kąt wewnętrzny tego trójkąta ma miarę
A) 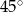 B)
B) 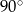 C)
C) 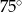 D)
D) 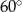
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 2:4:9. Największy kąt wewnętrzny tego trójkąta ma miarę
A) 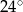 B)
B) 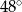 C)
C) 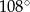 D)
D) 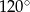
Naprzeciwko boków 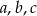 trójkąta
trójkąta 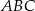 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 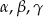 . Wiadomo, że
. Wiadomo, że 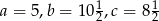 . Wówczas
. Wówczas
A) 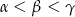 B)
B) 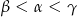 C)
C) 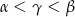 D)
D) 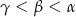
Naprzeciwko boków 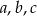 trójkąta
trójkąta 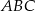 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 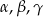 . Wiadomo, że
. Wiadomo, że 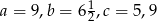 . Wówczas
. Wówczas
A) 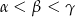 B)
B) 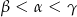 C)
C) 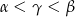 D)
D) 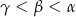
Naprzeciwko boków 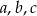 trójkąta
trójkąta 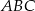 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 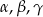 . Wiadomo, że
. Wiadomo, że 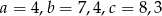 . Wówczas
. Wówczas
A) 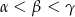 B)
B) 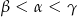 C)
C) 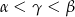 D)
D) 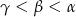
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 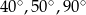 B)
B) 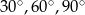 C)
C) 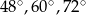 D)
D) 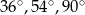
Na rysunku przedstawiono okrąg o środku 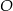 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 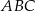 .
.
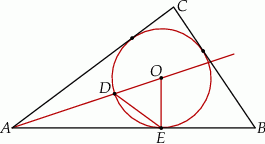
Okrąg ten przecina bok 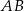 w punkcie
w punkcie 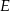 , a odcinek
, a odcinek 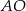 w punkcie
w punkcie 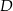 . Jeżeli
. Jeżeli 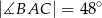 , to miara kąta
, to miara kąta 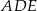 jest równa
jest równa
A) 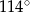 B)
B) 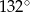 C)
C) 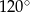 D)
D) 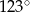
Jeden kąt trójkąta ma miarę 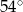 . Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
A) 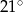 i
i 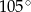 B)
B) 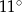 i
i 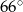 C)
C) 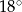 i
i 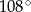 D)
D) 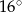 i
i 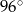
Jeden kąt trójkąta ma miarę 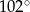 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 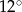 i
i 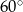 B)
B) 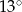 i
i 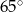 C)
C) 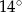 i
i 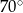 D)
D) 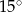 i
i 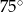
Jeden z kątów wewnętrznych trójkąta ma 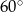 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 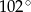 B)
B) 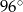 C)
C) 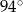 D)
D) 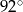
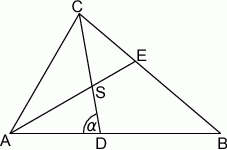
Dany jest trójkąt 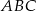 , w którym
, w którym 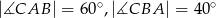 . Odcinki
. Odcinki 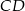 i
i 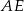 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 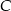 i
i 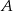 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
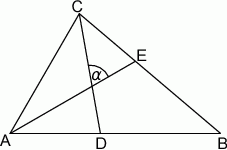
A) 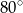 B)
B) 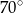 C)
C) 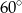 D)
D) 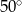
Dany jest trójkąt 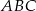 , w którym
, w którym 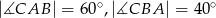 . Odcinki
. Odcinki 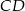 i
i 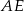 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 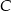 i
i 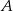 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
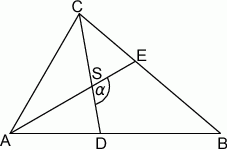
A) 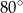 B)
B) 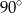 C)
C) 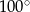 D)
D) 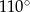
Dany jest trójkąt 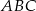 , w którym
, w którym 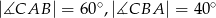 . Odcinki
. Odcinki 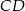 i
i 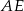 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 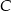 i
i 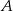 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 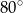 B)
B) 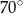 C)
C) 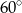 D)
D) 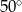
Punkty 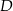 ,
, 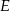 i
i 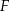 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 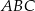 z jego bokami i
z jego bokami i 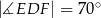 (zobacz rysunek).
(zobacz rysunek).
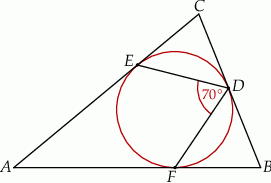
Miara kąta 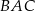 jest równa
jest równa
A) 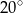 B)
B) 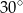 C)
C) 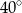 D)
D) 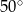
W trójkącie 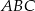 miary kątów wynoszą:
miary kątów wynoszą: 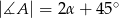 ,
, 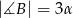 ,
, 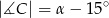 . Wówczas
. Wówczas
A) 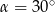 B)
B) 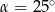 C)
C) 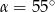 D)
D) 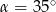
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 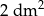 ?
?
A) 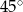 B)
B) 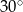 C)
C) 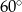 D)
D) 
Wiadomo, że sinus kąta  trójkąta przedstawionego na rysunku jest równy
trójkąta przedstawionego na rysunku jest równy 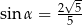 .
.
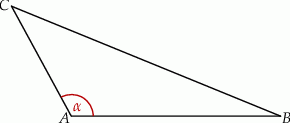
Wtedy
A) 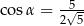 B)
B) 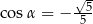 C)
C) 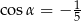 D)
D)