Obwód trójkąta 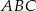 wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt
wynosi 24 cm. Połączono środki boków tego trójkąta i otrzymano trójkąt 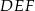 , którego obwód jest równy
, którego obwód jest równy
A) 6 cm B) 8 cm C) 12 cm D) 18 cm
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Dowolny/Oblicz długość
Trójkąt 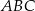 ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 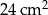 . Najdłuższa wysokość trójkąta
. Najdłuższa wysokość trójkąta 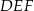 podobnego do trójkąta
podobnego do trójkąta 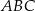 w skali 1:3 ma długość
w skali 1:3 ma długość
A) 4 cm B) 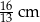 C) 2 cm D)
C) 2 cm D) 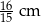
Środkowe w trójkącie 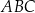 przecinają się w punkcie
przecinają się w punkcie 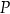 odległym od wierzchołka
odległym od wierzchołka 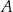 o 6 cm. Wobec tego środkowa poprowadzona na bok
o 6 cm. Wobec tego środkowa poprowadzona na bok 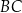 ma długość
ma długość
A) 12 cm B) 9 cm C) 15 cm D) 10 cm
Środkowe w trójkącie 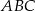 przecinają się w punkcie
przecinają się w punkcie 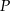 odległym od wierzchołka
odległym od wierzchołka 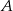 o 6 cm. Środkowa opuszczona na bok
o 6 cm. Środkowa opuszczona na bok 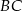 przecina ten bok w punkcie
przecina ten bok w punkcie 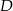 . Wobec tego długość odcinka
. Wobec tego długość odcinka 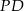 wynosi
wynosi
A) 1 cm B) 2 cm C) 3 cm D) 6 cm
Środkowe w trójkącie 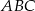 przecinają się w punkcie
przecinają się w punkcie 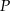 , przy czym długość środkowej opuszczonej na bok
, przy czym długość środkowej opuszczonej na bok 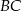 ma długość 9 cm. Wobec tego długość odcinka
ma długość 9 cm. Wobec tego długość odcinka 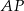 wynosi
wynosi
A) 6 cm B) 3 cm C) 2 cm D) 5 cm
Punkt 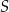 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 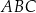 . Długość odcinka
. Długość odcinka 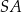 jest równa 10. Długość środkowej poprowadzonej z wierzchołka
jest równa 10. Długość środkowej poprowadzonej z wierzchołka 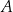 do boku
do boku 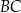 jest równa
jest równa
A) 10 B) 15 C) 20 D) 30
Oblicz długość odcinka 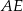 wiedząc, że
wiedząc, że 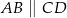 i
i 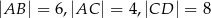 .
.
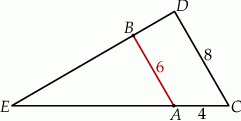
A) 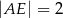 B)
B) 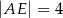 C)
C) 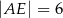 D)
D) 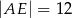
Oblicz długość odcinka 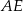 wiedząc, że
wiedząc, że 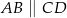 i
i 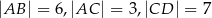 .
.
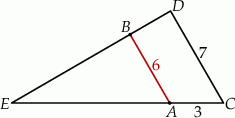
A) 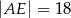 B)
B) 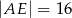 C)
C) 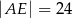 D)
D) 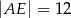
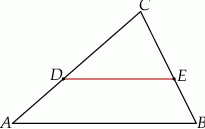
W trójkącie 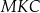 bok
bok 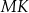 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 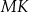 przecina boki
przecina boki 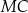 i
i 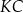 – odpowiednio – w punktach
– odpowiednio – w punktach 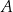 oraz
oraz 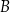 takich, że
takich, że 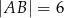 i
i 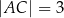 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 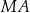 jest równa
jest równa
A) 18 B) 15 C) 9 D) 12
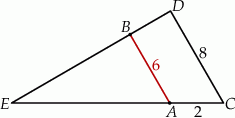
Oblicz długość odcinka 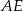 wiedząc, że
wiedząc, że 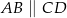 i
i 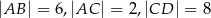 .
.
A) 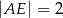 B)
B) 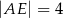 C)
C) 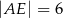 D)
D) 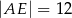
W trójkącie 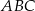 punkt
punkt 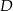 leży na boku
leży na boku 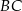 , a punkt
, a punkt 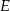 leży na boku
leży na boku 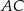 . Odcinek
. Odcinek 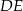 jest równoległy do boku
jest równoległy do boku 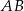 , a ponadto
, a ponadto 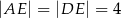 ,
, 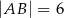 (zobacz rysunek).
(zobacz rysunek).
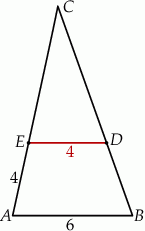
Odcinek 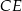 ma długość
ma długość
A) 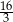 B)
B)  C) 8 D) 6
C) 8 D) 6
W trójkącie 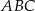 punkt
punkt 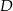 leży na boku
leży na boku 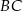 , a punkt
, a punkt 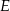 leży na boku
leży na boku 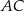 . Odcinek
. Odcinek 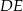 jest równoległy do boku
jest równoległy do boku 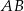 , a ponadto
, a ponadto 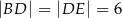 ,
, 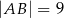 (zobacz rysunek).
(zobacz rysunek).
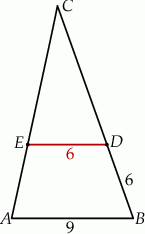
Odcinek 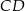 ma długość
ma długość
A) 8 B) 4 C) 9 D) 12
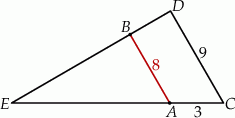
Oblicz długość odcinka 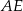 wiedząc, że
wiedząc, że 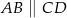 i
i 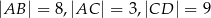 .
.
A) 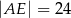 B)
B) 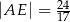 C)
C) 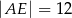 D)
D) 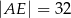
Jeżeli odcinki 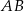 i
i 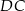 są równoległe, to długość odcinka
są równoległe, to długość odcinka 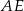 (patrz rys.) jest równa
(patrz rys.) jest równa
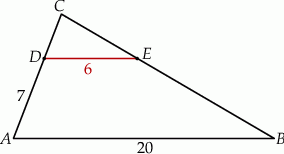
A) 9 B) 10 C) 11 D) 12
Odcinki 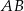 i
i 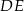 są równoległe. Długości odcinków
są równoległe. Długości odcinków 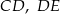 i
i 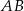 są odpowiednio równe 2, 5 i 15.
są odpowiednio równe 2, 5 i 15.
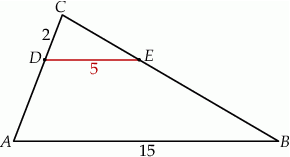
Długość odcinka 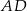 jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Odcinki 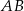 i
i 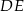 są równoległe. Długości odcinków
są równoległe. Długości odcinków 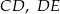 i
i 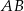 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
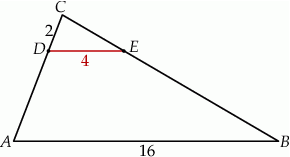
Długość odcinka 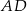 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Odcinki 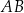 i
i 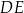 są równoległe. Długości odcinków
są równoległe. Długości odcinków 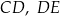 i
i 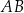 są odpowiednio równe 1, 3 i 9.
są odpowiednio równe 1, 3 i 9.
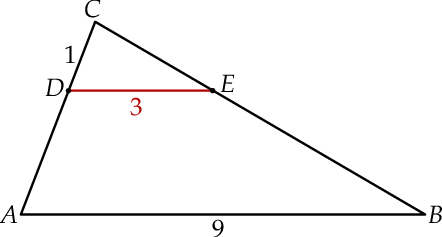
Długość odcinka 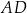 jest równa
jest równa
A) 2 B) 3 C) 5 D) 6
W trójkącie 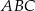 bok
bok 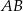 ma długość 4, a bok
ma długość 4, a bok 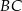 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 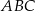 przecina bok
przecina bok 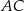 w punkcie
w punkcie 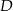 takim, że
takim, że 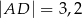 (zobacz rysunek).
(zobacz rysunek).
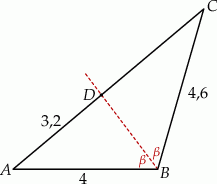
Odcinek 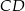 ma długość
ma długość
A) 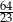 B)
B) 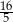 C)
C) 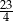 D)
D) 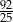
Odcinki 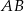 i
i 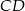 są równoległe. Długości odcinków
są równoległe. Długości odcinków 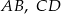 i
i 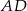 są podane na rysunku.
są podane na rysunku.
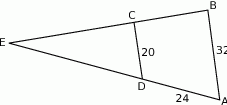
Długość odcinka 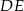 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
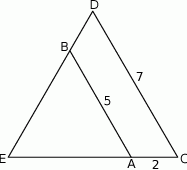
Odcinki 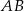 i
i 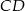 są równoległe i
są równoległe i 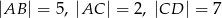 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 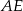 jest równa
jest równa
A) 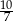 B)
B) 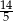 C) 3 D) 5
C) 3 D) 5
Odcinki 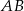 i
i 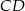 są równoległe i
są równoległe i 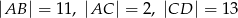 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 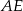 jest równa
jest równa
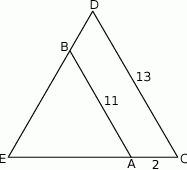
A) 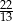 B)
B) 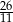 C) 11 D) 13
C) 11 D) 13
Odcinki 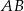 i
i 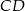 są równoległe. Długości odcinków
są równoległe. Długości odcinków 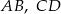 i
i 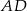 są podane na rysunku.
są podane na rysunku.
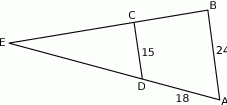
Długość odcinka 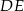 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
Dany jest trójkąt 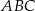 o bokach
o bokach 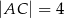 ,
, 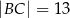 ,
, 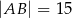 . Sinus kąta
. Sinus kąta 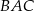 jest równy
jest równy  , a dwusieczne kątów
, a dwusieczne kątów 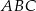 i
i 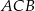 przecinają się w punkcie
przecinają się w punkcie 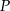 (zobacz rysunek).
(zobacz rysunek).
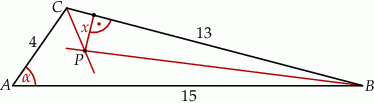
Odległość  punktu
punktu 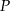 od prostej
od prostej 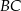 jest równa
jest równa
A) 2 B) 1 C)  D)
D) 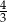
Pole trójkąta ostrokątnego o bokach 5 i 6 jest równe 9. Długość trzeciego boku tego trójkąta jest równa
A) 5 B) 6 C) 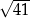 D)
D) 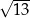
W trójkącie 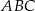 bok
bok 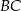 ma długość 13, a wysokość
ma długość 13, a wysokość 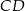 tego trójkąta dzieli bok
tego trójkąta dzieli bok 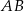 na odcinki o długościach
na odcinki o długościach 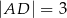 i
i 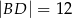 (zobacz rysunek obok).
(zobacz rysunek obok).
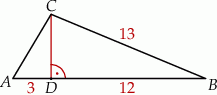
Długość boku 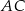 jest równa
jest równa
A) 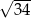 B)
B) 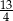 C)
C) 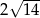 D)
D) 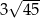
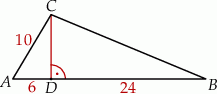
W trójkącie 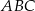 bok
bok 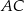 ma długość 10, a wysokość
ma długość 10, a wysokość 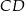 tego trójkąta dzieli bok
tego trójkąta dzieli bok 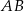 na odcinki o długościach
na odcinki o długościach 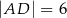 i
i 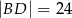 (zobacz rysunek obok).
(zobacz rysunek obok).
Długość boku 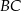 jest równa
jest równa
A) 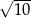 B)
B) 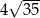 C)
C) 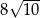 D)
D) 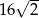
Liczby naturalne 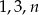 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 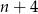 B)
B) 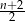 C)
C)  D) 3
D) 3
Liczby naturalne 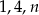 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 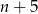 B)
B) 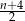 C) 4 D)
C) 4 D) 
Obwód trójkąta 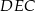 wynosi
wynosi 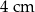 . Wiadomo, że
. Wiadomo, że 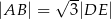 oraz
oraz 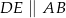 . Zatem obwód trójkąta
. Zatem obwód trójkąta 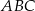 jest równy
jest równy
A) 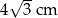 B)
B) 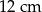 C)
C) 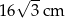 D)
D) 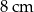
Obwód trójkąta 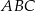 jest równy 40 cm. Punkt
jest równy 40 cm. Punkt 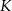 leży na boku
leży na boku 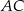 , a punkt
, a punkt 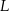 na boku
na boku 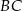 tak, że odcinek
tak, że odcinek 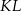 jest równoległy do boku
jest równoległy do boku 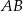 trójkąta i
trójkąta i 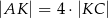 . Obwód trójkąta
. Obwód trójkąta 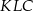 jest równy:
jest równy:
A) 10 cm B) 4 cm C) 8 cm D) 5 cm
Pole trójkąta, w którym wysokość jest o 3 cm dłuższa od podstawy jest równe 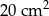 Wysokość trójkąta jest równa:
Wysokość trójkąta jest równa:
A) 5 cm B) 8 cm C) 2 cm D) 11 cm
W trójkącie 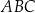 bok
bok 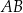 ma długość
ma długość 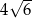 . Ponadto
. Ponadto 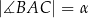 ,
, 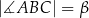 oraz
oraz 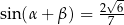 . Długość okręgu opisanego na trójkącie
. Długość okręgu opisanego na trójkącie 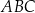 jest równa
jest równa
A) 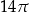 B)
B) 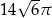 C)
C) 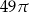 D)
D) 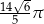
W trójkącie 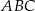 punkt
punkt 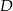 leży na boku
leży na boku 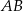 , punkt
, punkt 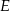 leży na boku
leży na boku 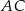 , a ponadto odcinek
, a ponadto odcinek 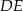 jest równoległy do boku
jest równoległy do boku 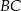 i
i 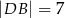 . Pole trójkąta
. Pole trójkąta 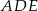 jest równe 12, a pole trapezu
jest równe 12, a pole trapezu 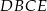 jest równe 15 (zobacz rysunek).
jest równe 15 (zobacz rysunek).
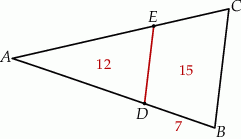
Odcinek 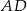 ma długość
ma długość
A) 5,6 B) 12 C) 14 D) 9
W trójkącie 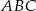 na rysunku obok dane są:
na rysunku obok dane są: 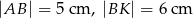 oraz
oraz 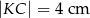 . Wiadomo, że
. Wiadomo, że 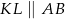 .
.
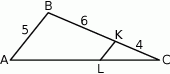
Wówczas:
A) 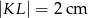 B)
B) 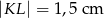 C)
C) 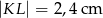 D)
D) 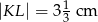
W trójkącie 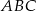 punkt
punkt 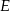 leży na boku
leży na boku 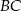 , a punkt
, a punkt 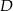 leży na boku
leży na boku 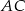 . Odcinek
. Odcinek 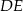 jest równoległy do boku
jest równoległy do boku 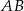 , a ponadto
, a ponadto 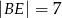 ,
, 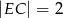 i
i 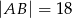 (zobacz rysunek).
(zobacz rysunek).
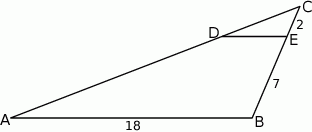
Długość odcinka 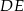 jest równa
jest równa
A) 5 B) 3 C) 6 D) 4
W trójkącie 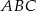 punkt
punkt 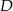 leży na boku
leży na boku 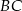 , a punkt
, a punkt 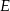 leży na boku
leży na boku 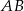 . Odcinek
. Odcinek 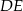 jest równoległy do boku
jest równoległy do boku 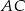 , a ponadto
, a ponadto  ,
, 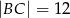 i
i 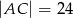 (zobacz rysunek).
(zobacz rysunek).
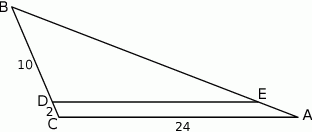
Długość odcinka 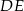 jest równa
jest równa
A) 22 B) 20 C) 12 D) 11
Dany jest trójkąt 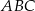 , w którym
, w którym 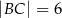 . Miara kąta
. Miara kąta 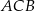 jest równa
jest równa 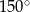 (zobacz rysunek).
(zobacz rysunek).
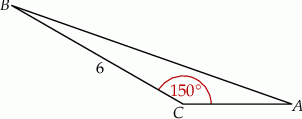
Wysokość trójkąta 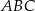 opuszczona z wierzchołka
opuszczona z wierzchołka 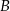 jest równa
jest równa
A) 3 B) 4 C) 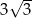 D)
D) 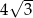
W trójkącie 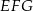 bok
bok 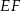 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 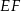 przecina boki
przecina boki 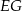 i
i 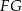 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 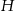 oraz
oraz 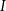 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 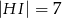 i
i 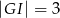 . Wtedy długość odcinka
. Wtedy długość odcinka 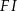 jest równa
jest równa
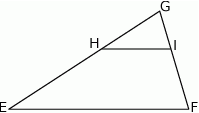
A) 6 B) 9 C) 12 D) 17
W trójkącie 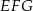 bok
bok 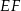 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 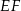 przecina boki
przecina boki 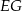 i
i 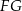 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 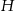 oraz
oraz 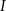 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 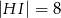 i
i 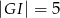 . Wtedy długość odcinka
. Wtedy długość odcinka 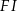 jest równa
jest równa
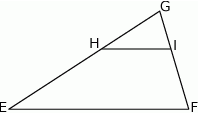
A) 6 B) 9 C) 10 D) 12
Odcinki 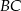 i
i 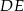 są równoległe i
są równoległe i 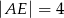 ,
, 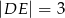 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 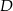 jest środkiem odcinka
jest środkiem odcinka 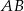 . Długość odcinka
. Długość odcinka 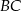 jest równa
jest równa
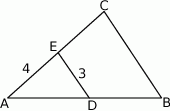
A) 4 B) 6 C) 8 D) 16
Odcinki 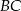 i
i 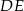 są równoległe i
są równoległe i 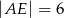 ,
, 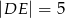 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 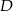 jest środkiem odcinka
jest środkiem odcinka 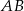 . Długość odcinka
. Długość odcinka 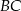 jest równa
jest równa
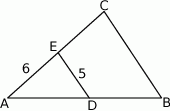
A) 10 B) 6 C) 8 D) 30
Dany jest trójkąt 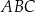 , w którym
, w którym 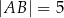 ,
, 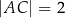 oraz
oraz 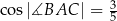 . Długość boku
. Długość boku 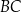 tego trójkąta jest równa
tego trójkąta jest równa
A) 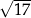 B)
B) 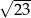 C)
C) 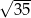 D)
D) 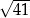
Z trójkąta 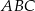 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 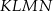 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
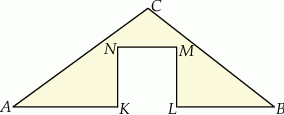
A) 64 B) 60 C) 75 D) 70

