Wyznacz najmniejszą i największą wartość funkcji 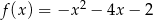 w przedziale
w przedziale 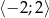 .
.
/Szkoła średnia/Funkcje/Kwadratowa/Ekstrema
Wyznacz najmniejszą i największą wartość funkcji 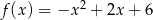 w przedziale
w przedziale 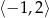 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 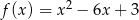 w przedziale
w przedziale 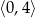 .
.
Oblicz najmniejszą i największą wartość funkcji 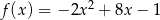 w przedziale
w przedziale 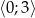 .
.
Wyznacz wartość największą i najmniejszą funkcji kwadratowej 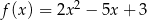 w przedziale
w przedziale 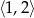 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 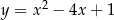 w przedziale
w przedziale 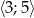 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 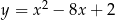 w przedziale
w przedziale 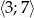 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 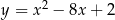 w przedziale
w przedziale 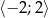 .
.
Oblicz najmniejszą i największą wartość funkcji 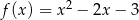 w przedziale
w przedziale 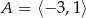 .
.
Oblicz najmniejszą i największą wartość funkcji 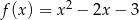 w przedziale
w przedziale 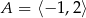 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 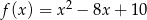 w przedziale
w przedziale 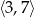 .
.
Wyznacz największą i najmniejszą wartość funkcji 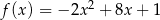 osiąganą w przedziale
osiąganą w przedziale 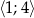 .
.
Wyznacz największą i najmniejszą wartość funkcji 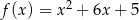 osiąganą w przedziale
osiąganą w przedziale 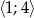 .
.
Oblicz największą i najmniejszą wartość funkcji 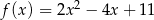 w przedziale
w przedziale 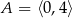 .
.
Oblicz najmniejszą i największą wartość funkcji 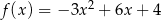 w przedziale
w przedziale 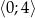 .
.
Wyznacz największą i najmniejszą wartość funkcji 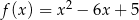 osiąganą w przedziale
osiąganą w przedziale 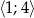 .
.
Określ zbiór wartości funkcji: 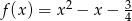 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 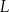 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
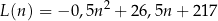
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 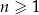 i
i 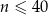 . Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
. Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
Właściciel pewnej piekarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 28 kolejnych dni. Przyjmijmy, że liczbę 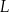 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
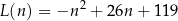
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 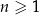 i
i 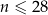 . W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
. W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
Dane są dwie funkcje kwadratowe 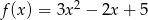 i
i 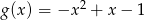 . Wyznacz największą wartość funkcji
. Wyznacz największą wartość funkcji 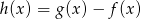 .
.
Wyznacz najmniejszą wartość funkcji 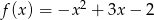 w przedziale
w przedziale 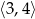 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 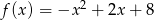 w przedziale
w przedziale 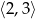 .
.
Wyznacz największą wartość funkcji 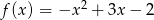 w przedziale
w przedziale 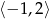 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 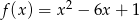 w przedziale
w przedziale 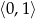 .
.
Wyznacz najmniejszą wartość funkcji 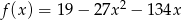 na przedziale
na przedziale 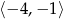 .
.
Oblicz największą wartość funkcji kwadratowej 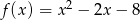 w przedziale
w przedziale 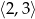 .
.
Oblicz największą wartość funkcji 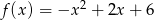 w przedziale
w przedziale 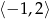 .
.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 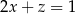 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 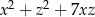 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Liczby rzeczywiste 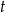 i
i 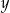 spełniają warunek
spełniają warunek 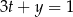 . Wyznacz takie wartości
. Wyznacz takie wartości 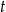 i
i 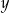 , dla których wyrażenie
, dla których wyrażenie 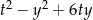 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Wyznacz zbiór wartości funkcji 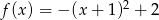 .
.
Wyznacz zbiór wartości funkcji 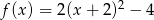 .
.
Wyznacz zbiór wartości funkcji 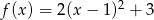 .
.
Wyznacz najmniejszą i największą wartość funkcji: 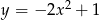 w przedziale
w przedziale 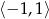 .
.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 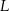 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
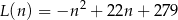
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 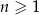 i
i 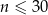 . Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
. Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
Wyznacz najmniejszą i największą wartość funkcji 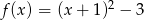 w przedziale
w przedziale 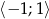 .
.
Wyznacz najmniejszą wartość funkcji kwadratowej 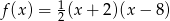 w przedziale
w przedziale 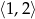 .
.
Wyznacz najmniejszą wartość funkcji 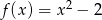 w przedziale
w przedziale 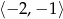 .
.
Funkcja kwadratowa jest określona wzorem 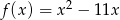 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 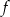 w przedziale
w przedziale 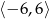 .
.
Funkcja kwadratowa jest określona wzorem 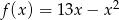 . Oblicz największą wartość funkcji
. Oblicz największą wartość funkcji 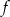 w przedziale
w przedziale 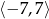 .
.
Wyznacz najmniejszą i największą wartość funkcji 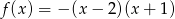 w przedziale
w przedziale 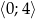 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 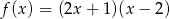 w przedziale
w przedziale 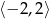 .
.
Wyznacz najmniejszą i największą wartość funkcji 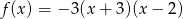 w przedziale
w przedziale 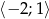 .
.
Wyznacz najmniejszą i największą wartość funkcji 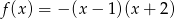 w przedziale
w przedziale 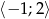 .
.

