Pięćdziesiąty wyraz ciągu arytmetycznego 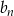 jest równy 5. Oblicz
jest równy 5. Oblicz 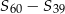 , gdzie
, gdzie 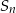 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 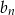 .
.
/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez kolejne wyrazy
Ciąg 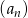 , gdzie
, gdzie 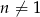 jest ciągiem arytmetycznym w którym
jest ciągiem arytmetycznym w którym 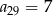 . Oblicz
. Oblicz 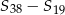 , gdzie
, gdzie 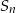 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 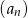 .
.
W ciągu arytmetycznym 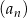 , określonym dla
, określonym dla 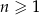 , dane są wyrazy:
, dane są wyrazy: 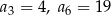 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których wyrazy ciągu
, dla których wyrazy ciągu 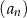 są mniejsze od 200.
są mniejsze od 200.
W ciągu arytmetycznym 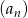 dane są wyrazy:
dane są wyrazy: 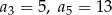 . Oblicz, ile wyrazów ciągu
. Oblicz, ile wyrazów ciągu 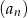 jest mniejszych niż 83.
jest mniejszych niż 83.
Pierwszy wyraz malejącego ciągu arytmetycznego 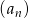 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu 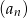 oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
W ciągu arytmetycznym suma pierwszego i trzeciego wyrazu jest równa 2, a iloraz pierwszego i czwartego jest równy 1.
- Napisz wzór ogólny ciągu oraz wzór na sumę
 początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu. - Wyznacz
 , dla których suma
, dla których suma  kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 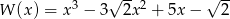 , a jednym z nich jest
, a jednym z nich jest 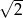 .
.
- Znajdź pierwszy wyraz tego ciągu.
- Oblicz sumę
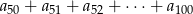 .
.
Ciąg 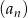 jest arytmetyczny oraz
jest arytmetyczny oraz 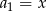 i
i 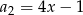 . Wiedząc, że
. Wiedząc, że 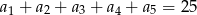 oblicz
oblicz  oraz sumę
oraz sumę 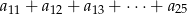 .
.
Znajdź ogólny wyraz ciągu arytmetycznego 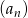 wiedząc, że
wiedząc, że 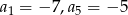 .
.
W rosnącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40. Wyznacz pierwszy wyraz tego ciągu.
Liczby 3 i 7 są dwoma początkowymi wyrazami pewnego rosnącego ciągu arytmetycznego. Oblicz dwudziesty wyraz tego ciągu i sumę jego dwudziestu początkowych wyrazów.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 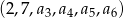 .
.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 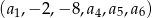 .
.
Oblicz wartości pozostałych wyrazów ciągu arytmetycznego: 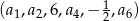 .
.
Oblicz sumę pierwszych 14 wyrazów ciągu arytmetycznego 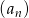 jeżeli
jeżeli 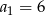 oraz
oraz 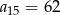 .
.
Oblicz sumę pierwszych 4 wyrazów ciągu arytmetycznego 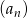 jeżeli
jeżeli 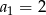 oraz
oraz 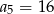
W ciągu arytmetycznym 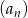 pierwszy wyraz
pierwszy wyraz 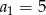 , a czwarty wyraz
, a czwarty wyraz 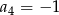 . Oblicz sumę dwudziestu początkowych wyrazów tego ciągu.
. Oblicz sumę dwudziestu początkowych wyrazów tego ciągu.
Pierwszy wyraz ciągu arytmetycznego jest równy 4, piąty wyraz tego ciągu jest równy 16. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
W ciągu arytmetycznym 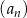 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 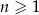 ,
, 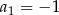 i
i 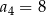 . Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
. Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
Pierwszy wyraz ciągu arytmetycznego jest równy 2, czwarty wyraz tego ciągu jest równy 14. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
Oblicz sumę pierwszych 10 wyrazów ciągu arytmetycznego 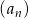 jeżeli
jeżeli 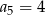 oraz
oraz 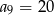 .
.
Pierwszy wyraz ciągu arytmetycznego jest równy 3, czwarty wyraz tego ciągu jest równy 15. Oblicz sumę sześciu początkowych wyrazów tego ciągu.
W ciągu arytmetycznym 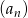 pierwszy wyraz
pierwszy wyraz 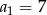 , a czwarty wyraz
, a czwarty wyraz 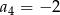 . Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
. Oblicz sumę osiemnastu początkowych wyrazów tego ciągu.
Oblicz sumę pierwszych 8 wyrazów ciągu arytmetycznego 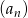 jeżeli
jeżeli 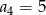 oraz
oraz 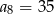 .
.
W ciągu arytmetycznym mamy dane 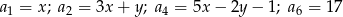 . Niech
. Niech 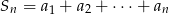 . Dla jakich
. Dla jakich  zachodzi równość
zachodzi równość 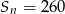 ?
?
Liczby
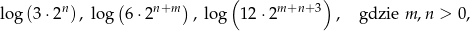
są odpowiednio pierwszym, piątym i dziewiątym wyrazem ciągu arytmetycznego. Wyznacz różnicę tego ciągu.
Dany jest ciąg arytmetyczny o pierwszym wyrazie 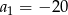 i różnicy
i różnicy 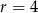 . Wyznacz liczbę
. Wyznacz liczbę  , dla której suma częściowa
, dla której suma częściowa 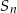 jest równa 780.
jest równa 780.
W ciągu arytmetycznym 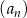 , określonym dla
, określonym dla 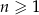 , wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Oblicz dla jakich wartości
, wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15. Oblicz dla jakich wartości  suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 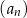 jest mniejsza od 729.
jest mniejsza od 729.
Liczby 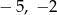 oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego
oraz 1 w podanej kolejności są trzema początkowymi wyrazami ciągu arytmetycznego 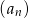 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 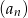 należy do przedziału
należy do przedziału 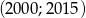 .
.
Liczby 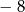 i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego
i 3 w podanej kolejności są dwoma początkowymi wyrazami ciągu arytmetycznego 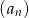 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 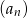 należy do przedziału
należy do przedziału 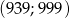 .
.
Drugi wyraz ciągu arytmetycznego jest równy 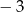 , dziesiąty wyraz jest równy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
, dziesiąty wyraz jest równy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
W ciągu arytmetycznym 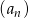 trzeci wyraz jest równy 11, a siódmy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
trzeci wyraz jest równy 11, a siódmy 21. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Wiedząc, że ciąg 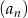 jest arytmetyczny i mając dane:
jest arytmetyczny i mając dane: 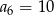 i
i 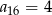 , oblicz
, oblicz 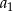 oraz różnicę
oraz różnicę  tego ciągu.
tego ciągu.
Trzeci wyraz ciągu arytmetycznego jest równy 10, a siódmy 42. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Dany jest ciąg arytmetyczny 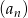 określony dla
określony dla 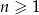 , w którym
, w którym 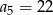 oraz
oraz 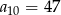 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 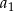 i różnicę
i różnicę  tego ciągu.
tego ciągu.
Znajdź ogólny wyraz ciągu arytmetycznego 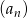 wiedząc, że
wiedząc, że 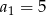 oraz
oraz 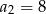 .
.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego jeśli 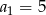 oraz
oraz 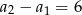 .
.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego 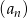 , jeśli
, jeśli 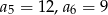 .
.
Oblicz sześć początkowych wyrazów ciągu arytmetycznego 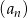 , jeśli
, jeśli 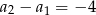 oraz
oraz 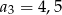 .
.
Oblicz 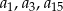 oraz sumę
oraz sumę 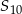 dziesięciu pierwszych wyrazów ciągu arytmetycznego
dziesięciu pierwszych wyrazów ciągu arytmetycznego 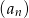 jeżeli
jeżeli 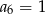 i
i 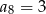 .
.
Oblicz 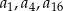 oraz sumę
oraz sumę 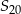 dwudziestu pierwszych wyrazów ciągu arytmetycznego
dwudziestu pierwszych wyrazów ciągu arytmetycznego 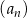 jeżeli
jeżeli 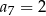 i
i 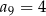 .
.
Oblicz 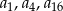 oraz sumę
oraz sumę 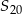 dwudziestu pierwszych wyrazów ciągu arytmetycznego
dwudziestu pierwszych wyrazów ciągu arytmetycznego 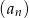 jeżeli
jeżeli 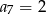 i
i 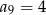 .
.

