Dane jest równanie 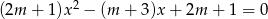 z niewiadomą
z niewiadomą  . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 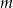 , dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.
, dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.
/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Nierówności z pierwiastkami
Wyznacz wszystkie wartości parametru 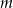 , dla których równanie
, dla których równanie 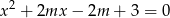 ma dwa różne pierwiastki należące do przedziału
ma dwa różne pierwiastki należące do przedziału 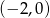 .
.
Dana jest funkcja kwadratowa 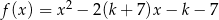 określona dla dowolnego
określona dla dowolnego 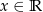 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 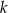 , dla których funkcja
, dla których funkcja 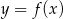 ma dwa różne miejsca zerowe należące do przedziału
ma dwa różne miejsca zerowe należące do przedziału 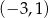 .
.
Wyznacz wszystkie wartości parametru 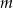 , dla których dwa różne pierwiastki rzeczywiste
, dla których dwa różne pierwiastki rzeczywiste 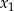 i
i 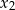 równania
równania 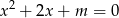 spełniają nierówność
spełniają nierówność 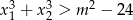 .
.
Dla jakiej wartości parametru 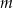 dwa różne pierwiastki
dwa różne pierwiastki 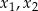 równania
równania
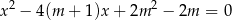
spełniają warunek 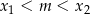 .
.
Wyznacz wszystkie wartości parametru 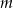 , dla których równanie
, dla których równanie 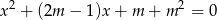 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 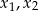 spełniające warunek:
spełniające warunek: 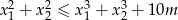 .
.
Wyznacz wszystkie wartości parametru 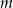 , dla których równanie
, dla których równanie 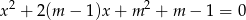 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 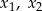 takie, że
takie, że 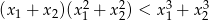 .
.
Dla jakich wartości parametru 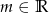 suma sześcianów dwóch różnych miejsc zerowych funkcji
suma sześcianów dwóch różnych miejsc zerowych funkcji 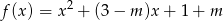 jest nieujemna?
jest nieujemna?
Wyznacz wszystkie wartości parametru 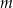 , dla których równanie
, dla których równanie
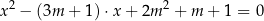
ma dwa różne rozwiązania rzeczywiste 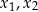 spełniające warunek
spełniające warunek
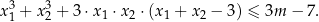
Dany jest trójmian kwadratowy 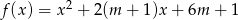 . Wyznacz wszystkie rzeczywiste wartości parametru
. Wyznacz wszystkie rzeczywiste wartości parametru 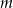 , dla których ten trójmian ma dwa różne pierwiastki
, dla których ten trójmian ma dwa różne pierwiastki 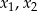 tego samego znaku, spełniające warunek
tego samego znaku, spełniające warunek 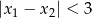 .
.
Dany jest trójmian kwadratowy 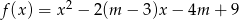 . Wyznacz wszystkie rzeczywiste wartości parametru
. Wyznacz wszystkie rzeczywiste wartości parametru 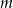 , dla których ten trójmian ma dwa różne pierwiastki
, dla których ten trójmian ma dwa różne pierwiastki 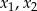 tego samego znaku, spełniające warunek
tego samego znaku, spełniające warunek 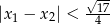 .
.
Wyznacz wszystkie wartości parametru 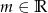 , dla których równanie
, dla których równanie 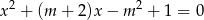 ma dwa różne pierwiastki
ma dwa różne pierwiastki 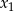 i
i 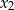 takie, że
takie, że 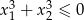 .
.
Wyznacz wszystkie wartości parametru 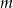 , dla których równanie
, dla których równanie 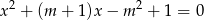 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 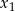 i
i 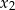
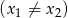 , spełniające warunek
, spełniające warunek 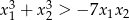 .
.
Wyznacz wszystkie wartości parametru 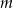 , dla których równanie
, dla których równanie
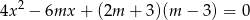
ma dwa różne rozwiązania rzeczywiste 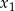 i
i 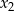 , przy czym
, przy czym 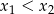 , spełniające warunek
, spełniające warunek
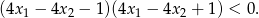
Wyznacz wszystkie wartości parametru 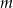 , dla których równanie
, dla których równanie
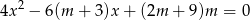
ma dwa różne rozwiązania rzeczywiste 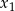 i
i 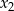 , przy czym
, przy czym 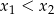 , spełniające warunek
, spełniające warunek
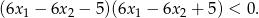
Dla jakich wartości parametru 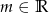 suma odwrotności kwadratów dwóch różnych miejsc zerowych funkcji
suma odwrotności kwadratów dwóch różnych miejsc zerowych funkcji 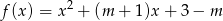 jest większa od 1?
jest większa od 1?
Wyznacz wszystkie wartości parametru 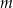 , dla których równanie
, dla których równanie
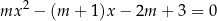
ma dokładnie dwa różne rozwiązania rzeczywiste 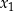 oraz
oraz 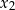 , spełniające warunki:
, spełniające warunki:
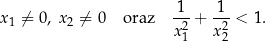
Wyznacz wszystkie wartości parametru 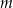 , dla których równanie
, dla których równanie
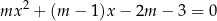
ma dokładnie dwa różne rozwiązania rzeczywiste 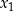 oraz
oraz 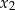 , spełniające warunki:
, spełniające warunki:
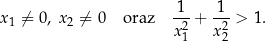
Wyznacz wszystkie wartości 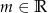 , dla których równanie
, dla których równanie 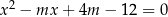 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność
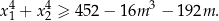
Wyznacz wszystkie wartości parametru 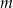 , dla których równanie
, dla których równanie
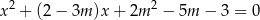
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 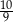 .
.
Dla jakich wartości parametru 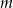 równanie
równanie 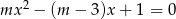 ma różne pierwiastki
ma różne pierwiastki 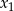 i
i 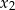 spełniające warunek
spełniające warunek 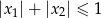 ?
?
Dla jakich wartości parametru 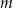 równanie
równanie 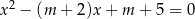 ma dwa pierwiastki różnych znaków
ma dwa pierwiastki różnych znaków 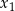 i
i 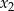 spełniające warunek
spełniające warunek 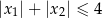 ?
?
Wyznacz wszystkie wartości parametru 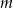 , dla których równanie
, dla których równanie 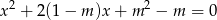 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 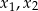 spełniające warunek
spełniające warunek 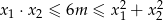 .
.
Wyznacz wszystkie wartości parametru 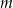 , dla których równanie
, dla których równanie
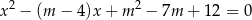
ma dwa różne rozwiązania rzeczywiste 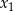 oraz
oraz 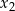 , spełniające warunek
, spełniające warunek
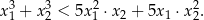
Wyznacz wszystkie wartości parametru 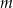 , dla których równanie
, dla których równanie 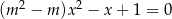 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 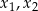 takie, że
takie, że 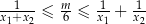 .
.
Wyznacz wszystkie wartości parametru 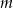 , dla których równanie
, dla których równanie 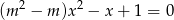 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 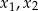 takie, że
takie, że 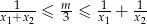 .
.
Wyznacz wszystkie wartości parametru 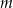 , dla których równanie
, dla których równanie
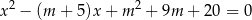
ma dwa różne rozwiązania rzeczywiste 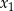 oraz
oraz 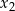 , spełniające warunek
, spełniające warunek
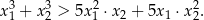
Wyznacz wszystkie wartości parametru 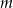 , dla których równanie
, dla których równanie 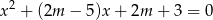 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 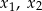 takie, że
takie, że 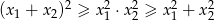 .
.
Wyznacz wszystkie wartości parametru 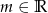 , dla których równanie
, dla których równanie 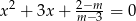 ma dwa różne pierwiastki
ma dwa różne pierwiastki 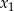 i
i 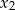 takie, że
takie, że 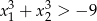 .
.
Wyznacz wszystkie wartości parametru 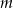 , dla których równanie
, dla których równanie 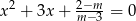 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 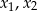 spełniające warunek
spełniające warunek 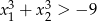 .
.
Wyznacz wszystkie wartości parametru 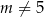 , dla których równanie
, dla których równanie
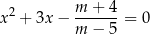
ma dwa różne rozwiązania rzeczywiste 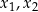 spełniające warunek
spełniające warunek 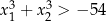 .
.
Wyznacz wszystkie wartości parametru 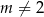 , dla których równanie
, dla których równanie
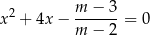
ma dwa różne rozwiązania rzeczywiste 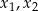 spełniające warunek
spełniające warunek 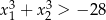 .
.
Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 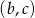 , takich, że równanie
, takich, że równanie 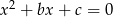 ma dwa różne rozwiązania należące do przedziału
ma dwa różne rozwiązania należące do przedziału 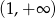 .
.
Wyznacz wszystkie wartości parametru 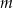 , dla których równanie
, dla których równanie
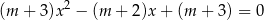
ma dwa różne rozwiązania 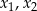 spełniające nierówność:
spełniające nierówność: 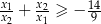 .
.
Dla jakich wartości parametru 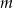 równanie
równanie 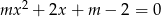 ma dwa różne pierwiastki mniejsze od 1?
ma dwa różne pierwiastki mniejsze od 1?
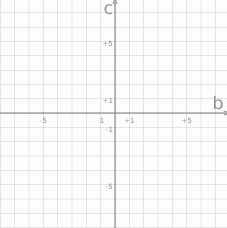
W prostokątnym układzie współrzędnych narysuj zbiór tych wszystkich punktów o współrzędnych 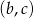 , dla których różne pierwiastki
, dla których różne pierwiastki 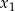 i
i 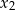 równania
równania 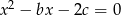 spełniają warunek
spełniają warunek 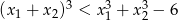 .
.
Dla jakich wartości parametru 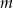 funkcja
funkcja 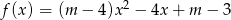 ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
Wyznacz te wartości parametru 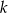 , dla których równanie
, dla których równanie 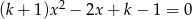 ma dwa różne rozwiązania należące do przedziału
ma dwa różne rozwiązania należące do przedziału 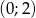 .
.

