Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?
/Szkoła średnia/Zadania z treścią/Prędkość/2 ruchome obiekty
Ukryj
Podobne zadania
Ala jeździ do szkoły rowerem, a Ola skuterem. Obie pokonują tę samą drogę. Ala wyjechała do szkoły o godzinie 7:00 i pokonała całą drogę w ciągu 40 minut. Ola wyjechała 10 minut później niż Ala, a pokonanie całej drogi zajęło jej tylko 20 minut. Oblicz, o której godzinie Ola wyprzedziła Alę.
W zbiorniku zamontowano dwie pompy: pierwsza z nich służy do napełniania zbiornika, a druga do jego opróżniania. Pierwsza pompa napełnia cały zbiornik w ciągu 30 minut, a druga opróżnia cały zbiornik w ciągu 20 minut. W pustym zbiorniku uruchamiamy pierwszą pompę, a po 5 minutach jej pracy uruchamiamy również drugą pompę. Po ilu minutach zbiornik będzie ponownie pusty?
Z tego samego miejsca wyruszyli w tę samą stronę piechur i rowerzysta. Piechur wyszedł o godzinie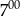 
i maszerował z prędkością 5 km/h, a rowerzysta wyjechał o godzinie 
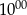i jechał z prędkością 15 km/h. O której godzinie rowerzysta dogonił piechura?
Ze Szczecina do Częstochowy wybrały się dwie pielgrzymki: piesza i rowerowa. Pielgrzymka piesza wyruszyła pierwsza, pokonując każdego dnia 26 km. Po 8 dniach wyruszyła (z tego samego miejsca, tą samą trasą) pielgrzymka rowerowa, pokonując pierwszego dnia 54 km, a każdego następnego dnia o 2 kilometry mniej niż dnia poprzedniego. Pielgrzymki spotkały się dopiero u stóp Jasnej Góry. W którym dniu podróży i w jakiej odległości od miejsca wyjazdu pielgrzymka rowerowa dogoniła pielgrzymkę pieszą?
Z dwóch miejscowości 
i 
wyruszyły naprzeciw siebie ruchem jednostajnym dwa pociągi. Po upływie trzech godzin minęły się. Pierwszy pociąg przejechał trasę z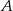 
do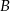 
w ciągu 7,5 godziny. W jakim czasie drogę z 
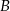do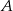 
przejechał drugi pociąg?
Samochód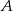 
, jadący pod górę, w pierwszej sekundzie pokonał 25 m, a w każdej następnej o pół metra mniej niż w poprzedniej. W tym samym momencie, gdy 
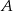rozpoczął podjazd, zjazd z góry rozpoczął samochód 
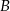, będący w odległości 360 m od 
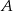. Samochód 
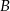w pierwszej sekundzie przebył drogę 9 m, a w każdej następnej o 2 m więcej niż w poprzedniej. Jaką odległość pokonał samochód 
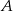do chwili minięcia z samochodem 
?
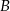Droga z miejscowości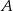 
do miejscowości 
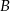ma długość 26 km. Motocyklista przebył tę drogę w czasie o 1,5 h krótszym niż rowerzysta, który jechał z prędkością o 39 km/h mniejszą. Oblicz, z jaką prędkością jechał motocyklista, a z jaką rowerzysta.
Ukryj
Podobne zadania
Trasę etapu wyścigu kolarskiego o długości 150 km pan Nowak pokonał w czasie o 1 godzinę i 50 minut krótszym niż jego kolega z drużyny, pan Kowalski. Średnia wartość prędkości, z jaką pan Nowak jechał na tym etapie, była o 11 km/h większa od średniej wartości prędkości pana Kowalskiego na tej trasie. Oblicz średnie wartości prędkości, z jakimi przejechali całą trasę obaj zawodnicy.
Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.
Dwa miasta łączy droga o długości 448 kilometrów. Samochód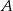 
przebył tę trasę w czasie o 40 minut krótszym niż samochód 
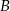. Średnia prędkość samochodu 
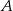na tej trasie była o 12 km/h większa od średniej prędkości samochodu 
. Oblicz średnią prędkość każdego z tych samochodów na tej trasie.
Miasta 
i 
są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
– prędkości, z jaką pani Danuta jechała z A do B.
– prędkości, z jaką pani Lidia jechała z A do B.
Pociąg towarowy pokonał trasę długości 208 km. Gdyby średnia prędkość pociągu była większa o 13 km/h to tę samą trasę pociąg pokonałby w czasie o 48 minut krótszym. Oblicz średnią prędkość z jaką pociąg pokonał tę trasę.
Dwóch motocyklistów wyrusza jednocześnie z tego samego miejsca. Jeden porusza się z prędkością 60 km/h i jedzie w kierunku wschodnim, a drugi z prędkością 80 km/h jedzie na północ. Po jakim czasie odległość między nimi (mierzona w linii prostej) będzie równa 300 km?
Ukryj
Podobne zadania
Dwóch rowerzystów wyrusza jednocześnie z tego samego miejsca. Jeden porusza się z prędkością 15 km/h i jedzie w kierunku wschodnim, a drugi z prędkością 20 km/h jedzie na północ. Po jakim czasie odległość między nimi (mierzona w linii prostej) będzie równa 75 km?
W biegu narciarskim na 30 km różnica czasów między zwycięzcą i ostatnim zawodnikiem była równa 20 min. Po biegu obliczono, że średnia prędkość zwycięzcy była o 3 km/h większa od prędkości ostatniego biegacza. Oblicz prędkość zwycięzcy.
Ukryj
Podobne zadania
Biegacz narciarski Borys wyruszył na trasę biegu o 10 minut później niż inny zawodnik, Adam. Metę zawodów, po przebyciu 15–kilometrowej trasy biegu, obaj zawodnicy pokonali równocześnie. Okazało się, że wartość średniej prędkości na całej trasie w przypadku Borysa była o 4,5 km/h większa niż w przypadku Adama. Oblicz, w jakim czasie Adam pokonał całą trasę biegu.
Dwaj turyści przebyli te samą trasę długości 15 km. Drugi turysta szedł z prędkością o 1 km/h mniejszą niż pierwszy, przez co trasę tę pokonał w czasie o 1 godzinę i 15 minut dłuższym niż pierwszy turysta. Oblicz średnią prędkość pierwszego turysty na tej trasie.
Paweł i Gaweł wyruszyli w 500 kilometrową podróż dwoma samochodami. Samochód Pawła poruszał się cały czas ze stałą prędkością, a sposób poruszania się samochodu Gawła przedstawiony jest na poniższym wykresie.
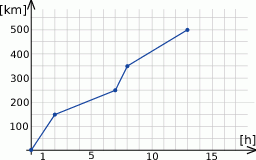
- Oblicz z jaką prędkością poruszał się samochód Pawła, jeżeli dojechał on do celu 20 minut po Gawle. Wynik podaj w kilometrach na godzinę
- Przez ile godzin Gaweł jechał wolniej od Pawła?
- Ile razy, i w której minucie podróży oba samochody się spotkały (nie licząc początku i końca podróży). Wynik podaj z dokładnością do 1 minuty.
Z miejscowośc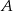i 
i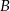 
, które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.
Dwa pociągi towarowe wyjechały z miast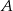 
i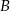 
oddalonych od siebie o 540 km. Pociąg jadący z miasta 
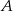do miasta 
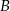wyjechał o godzinę wcześniej niż pociąg jadący z miasta 
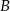do miasta 
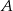i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
Ukryj
Podobne zadania
Dwa samochody osobowe wyjechały z miast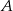 
i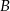 
oddalonych od siebie o 480 km. Samochód jadący z miasta 
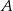do miasta 
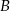wyjechał o pół godziny wcześniej niż samochód jadący z miasta 
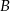do miasta 
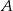i jechał z prędkością o 16 km/h mniejszą. Samochody te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te samochody.
Dwa motocykle wyjechały z miast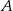 
i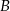 
oddalonych od siebie o 360 km. Motocykl jadący z miasta 
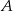do miasta 
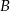wyjechał o 30 minut wcześniej niż motocykl jadący z miasta 
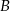do miasta 
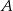i jechał z prędkością o 12 km/h mniejszą. Motocykle te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te motocykle.
Karawana o długości 1 km jedzie przez pustynię z prędkością 4 km/h. Co jakiś czas od czoła karawany do jej końca i z powrotem jedzie goniec z prędkością 6 km/h. Oblicz długość drogi tam i z powrotem, którą pokonuje goniec. Oblicz, ile czasu zajmuje mu przebycie tej drogi.
Dwaj rowerzyści wyjechali naprzeciw siebie z dwóch miejscowośc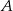i 
i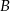 
położonych od siebie w odległości 180 km. Rowerzysta jadący z miejscowości 
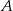wyjechał o godzinę później od drugiego i jechał ze średnią prędkością 3 km/h mniejszą niż rowerzysta jadący z miejscowości 
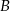. Stosunek średnich prędkości rowerzystów wyrażał się liczbą z przedziału 
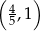. Rowerzyści spotkali się w odległości 72 km od miejscowości 
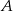. Z jakimi średnimi prędkościami jechali obaj rowerzyści?
Z miejscowośc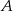i 
i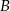 
oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości 
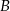do miejscowości 
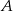jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości 
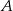do miejscowości 
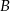wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości 
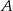przebył do tego miejsca 
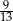całej drogi z 
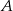do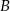 
. Z jakimi średnimi prędkościami jechali obaj rowerzyści?
Droga z miasta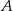 
do miasta 
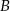ma długość 474 km. Samochód jadący z miasta 
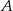do miasta 
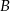wyrusza godzinę później niż samochód z miasta 
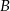do miasta 
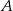. Samochody te spotykają się w odległości 300 km od miasta 
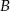. Średnia prędkość samochodu, który wyjechał z miasta 
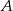, liczona od chwili wyjazdu z 
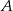do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z 
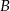do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.
Ukryj
Podobne zadania
Linia kolejowa między miastam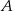i 
i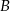 
ma długość 711 km. Pociąg jadący z miasta 
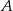do miasta 
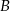wyrusza 45 minut później niż pociąg jadący z miasta 
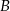do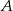 
. Pociągi te spotykają się w odległości 450 km od miasta 
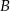. Średnia prędkość pociągu, który wyjechał z miasta 
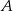, liczona od chwili wyjazdu z 
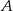do momentu spotkania, była o 34 km/h mniejsza od średniej prędkości drugiego pociągu liczonej od chwili wyjazdu z miasta 
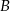do chwili spotkania. Oblicz średnią prędkość każdego z pociągów w chwili spotkania.
Z miast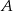 
i 
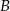odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta 
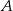wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta 
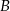. Samochody te minęły się w odległości 168 km licząc od miasta 
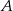. Oblicz średnią prędkość każdego z samochodów.
Dwa pociągi: towarowy o długości 490 m i osobowy o długości 210 m, jadą naprzeciw siebie po dwóch równoległych torach i spotykają się w miejscu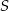 
. Mijanie się pociągów trwa 20 s, a czas przejazdu pociągu osobowego przez miejsce 
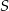jest o 25 sekund krótszy od czasu przejazdu pociągu towarowego. Oblicz prędkości obu pociągów, zakładając, że poruszają się ruchem jednostajnym.
Trasa rowerowa wokół jeziora ma długość 15 km. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro poruszając się w tym samym kierunku. Średnia prędkość drugiego z nich jest większa od średniej prędkości pierwszego o 5 km/h. Oblicz po jakim czasie dojdzie do ponownego spotkania rowerzystów.
Dwa samochody odbyły podróż z miejscowości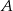 
do odległej o 480 km miejscowości 
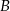. Drugi z samochodów jechał ze średnią prędkością większą o 20 km/h od średniej prędkości pierwszego samochodu, a czas przejazdu pierwszego samochodu był o 72 minuty dłuższy od czasu przejazdu drugiego samochodu. Oblicz ile czasu zajęła podróż każdemu z samochodów.
Ukryj
Podobne zadania
Dwa samochody odbyły podróż z miejscowości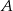 
do odległej o 252 km miejscowości 
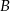. Średnia prędkość samochodu osobowego na tej trasie była o 24 km/h większa od średniej prędkości samochodu ciężarowego. Oblicz ile czasu zajęła podróż samochodowi osobowemu jeżeli pokonał on tę trasę w czasie o 72 minuty krótszym niż samochód ciężarowy.
Miasto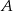 
i miasto 
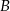łączy linia kolejowa długości 210 km. Średnia prędkość pociągu pospiesznego na tej trasie jest o 24 km/h większa od średniej prędkości pociągu osobowego. Pociąg pospieszny pokonuje tę trasę o 1 godzinę krócej niż pociąg osobowy. Oblicz czas pokonania tej drogi przez pociąg pospieszny.
Dwóch turystów przebyło tę samą trasę o długości 84 km, przy czym każdy z nich przechodził dziennie tę samą liczbę kilometrów. Pokonanie tej trasy zajęło drugiemu turyście o 3 dni dłużej niż pierwszemu, a pierwszy turysta przechodził dziennie o 9 km więcej od drugiego. Oblicz, ile kilometrów dziennie przechodził każdy z turystów.
Z dwóch miast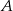 
i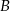 
, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta 
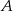o jedną godzinę wcześniej niż drugi z miasta 
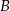. Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta 
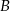jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta 
.
Ukryj
Podobne zadania
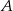Z dwóch miast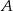 
i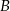 
odległych od siebie o 90 km wyjechali rowerami dwaj znajomi, by spotkać się o umówionej godzinie w miejscowości 
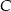, znajdującej się między 
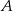i 
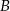. Pierwszy (z 
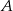) wyjechał o godzinę później niż drugi. W jakiej odległości od 
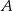znajduje się 
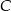, jeśli wiemy, że gdyby znajomi kontynuowali podróż (po spotkaniu w 
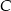), każdy w wybranym wcześniej kierunku i z dotychczasową szybkością, to pierwszy dotarłby do 
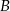po półtorej godziny, zaś drugi do 
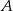– po 4 godzinach?
Po torze wodnym o długości 10 km pływają w kółko dwie łodzie motorowe, przy czym druga z nich płynie z prędkością o 5 km/h większą od prędkości pierwszej łodzi. Łodzie te wystartowały z tego samego punktu i ponownie spotkały się, gdy pierwsza z łodzi wykonała pełne 3 okrążenia toru. Oblicz średnie prędkości obu łodzi.
Ukryj
Podobne zadania
Trasa rowerowa wokół jeziora ma długość 12 kilometrów. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro w tym samym kierunku. Średnia prędkość jednego z nich jest o 4 km/h mniejsza niż prędkość drugiego rowerzysty. Do ponownego spotkania rowerzystów doszło, gdy szybszy z nich wykonał 4 okrążenia jeziora. Jakie były średnie prędkości rowerzystów?
