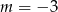Na której z podanych prostych leżą wszystkie punkty o współrzędnych 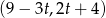 , gdzie
, gdzie 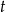 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 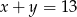 B)
B) 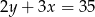 C)
C) 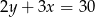 D)
D) 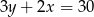
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Punkty na prostej
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 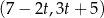 , gdzie
, gdzie 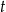 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 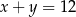 B)
B) 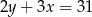 C)
C) 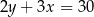 D)
D) 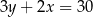
Punkt 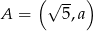 należy do prostej o równaniu
należy do prostej o równaniu 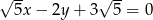 . Wynika stąd, że
. Wynika stąd, że
A) 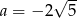 B)
B) 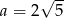 C)
C) 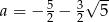 D)
D) 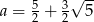
Punkt 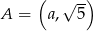 należy do prostej o równaniu
należy do prostej o równaniu 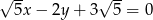 . Wynika stąd, że
. Wynika stąd, że
A) 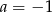 B)
B) 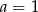 C)
C) 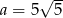 D)
D) 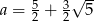
Punkt 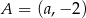 leży na prostej określonej równaniem
leży na prostej określonej równaniem 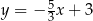 . Stąd wynika, że
. Stąd wynika, że
A) 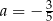 B)
B) 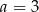 C)
C) 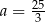 D)
D) 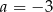
Punkt 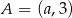 leży na prostej określonej równaniem
leży na prostej określonej równaniem 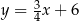 . Stąd wynika, że
. Stąd wynika, że
A) 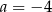 B)
B) 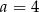 C)
C) 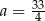 D)
D) 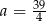
Punkt 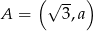 należy do prostej o równaniu
należy do prostej o równaniu 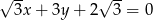 . Wynika stąd, że
. Wynika stąd, że
A) 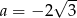 B)
B) 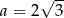 C)
C) 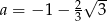 D)
D) 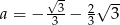
Na rysunku przedstawiono fragment prostej o równaniu 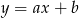 .
.
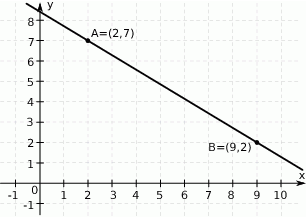
Punkt 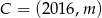 leży na tej prostej. Zatem
leży na tej prostej. Zatem
A) 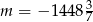 B)
B) 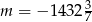 C)
C) 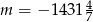 D)
D) 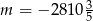
Na prostej 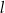 o współczynniku kierunkowym
o współczynniku kierunkowym 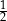 leżą punkty
leżą punkty 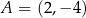 oraz
oraz 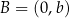 . Wtedy liczba
. Wtedy liczba 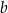 jest równa
jest równa
A) 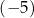 B) 10 C)
B) 10 C) 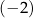 D) 0
D) 0
Punkty 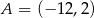 ,
, 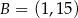 i
i 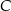 leżą na jednej prostej. Punkt
leżą na jednej prostej. Punkt 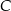 może mieć współrzędne
może mieć współrzędne
A) 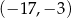 B)
B) 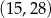 C)
C) 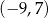 D)
D) 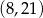
Na rysunku przedstawiono fragment prostej o równaniu 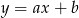 .
.
Współczynnik kierunkowy tej prostej jest równy
A) 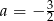 B)
B) 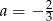 C)
C) 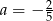 D)
D) 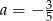
Na rysunku przedstawiono fragment prostej o równaniu 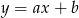 .
.
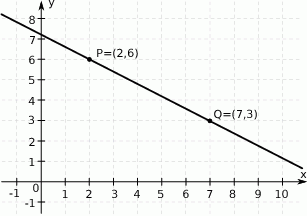
Współczynnik kierunkowy tej prostej jest równy
A) 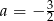 B)
B) 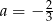 C)
C) 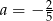 D)
D) 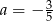
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 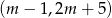 , gdzie
, gdzie 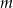 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 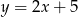 B)
B) 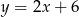 C)
C) 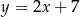 D)
D) 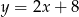
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 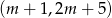 , gdzie
, gdzie 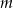 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 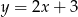 B)
B) 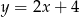 C)
C) 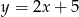 D)
D) 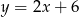
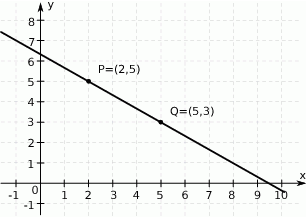
Na rysunku przedstawiony jest fragment prostej o równaniu 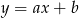 przechodzącej przez punkty
przechodzącej przez punkty 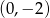 i
i 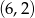 .
.
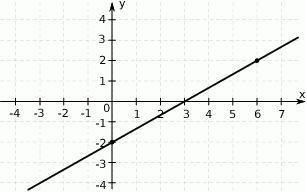
Wtedy
A) 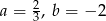 B)
B) 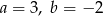 C)
C) 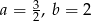 D)
D) 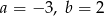
Na rysunku przedstawiony jest fragment prostej o równaniu 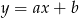 przechodzącej przez punkty
przechodzącej przez punkty 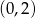 i
i 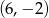 .
.
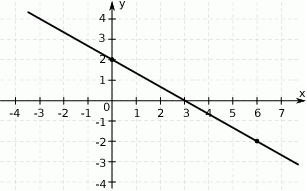
Wtedy
A) 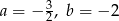 B)
B) 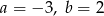 C)
C) 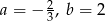 D)
D) 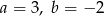
Równanie prostej przechodzącej przez punkty 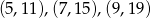 to
to
A) 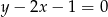 B)
B) 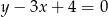 C)
C) 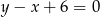 D)
D) 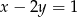
Punkt 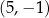 należy do prostej
należy do prostej 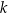 , której współczynnik kierunkowy jest równy
, której współczynnik kierunkowy jest równy 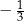 . Wskaż punkt, który nie należy do prostej
. Wskaż punkt, który nie należy do prostej 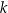 .
.
A) 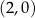 B)
B) 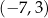 C)
C) 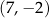 D)
D) 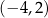
Wiadomo, że prosta o równaniu 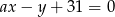 przechodzi przez środek odcinka o końcach
przechodzi przez środek odcinka o końcach 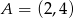 i
i 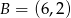 . Wówczas wartość współczynnika
. Wówczas wartość współczynnika  jest równa
jest równa
A) 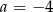 B)
B) 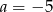 C)
C) 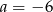 D)
D) 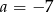
Dane są punkty 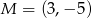 oraz
oraz 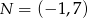 . Prosta przechodząca przez te punkty ma równanie
. Prosta przechodząca przez te punkty ma równanie
A) 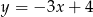 B)
B) 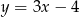 C)
C) 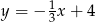 D)
D) 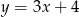
Prosta przechodząca przez punkty 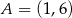 i
i 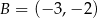 jest określona równaniem
jest określona równaniem
A) 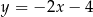 B)
B) 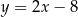 C)
C) 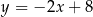 D)
D) 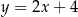
Prosta przechodząca przez punkty 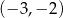 oraz
oraz 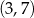 ma równanie
ma równanie
A) 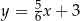 B)
B) 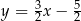 C)
C) 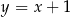 D)
D) 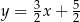
Prosta przechodząca przez punkty 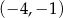 oraz
oraz 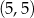 ma równanie
ma równanie
A) 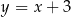 B)
B) 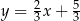 C)
C) 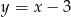 D)
D) 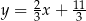
Prosta przechodząca przez punkty 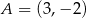 i
i 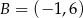 jest określona równaniem
jest określona równaniem
A) 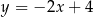 B)
B) 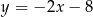 C)
C) 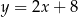 D)
D) 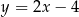
Punkty 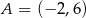 oraz
oraz 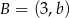 leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy
leżą na prostej, która przechodzi przez początek układu współrzędnych. Wtedy 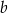 jest równe
jest równe
A) 9 B) 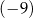 C)
C) 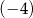 D) 4
D) 4
Punkt 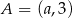 leży poniżej prostej określonej równaniem
leży poniżej prostej określonej równaniem 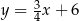 . Stąd wynika, że
. Stąd wynika, że
A) 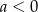 B)
B) 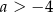 C)
C) 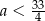 D)
D) 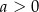
Punkt 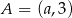 leży powyżej prostej określonej równaniem
leży powyżej prostej określonej równaniem 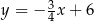 . Stąd wynika, że
. Stąd wynika, że
A) 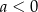 B)
B) 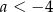 C)
C) 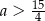 D)
D) 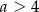
W układzie współrzędnych dane są dwa punkty 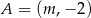 oraz
oraz 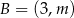 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 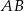 jest równy
jest równy  . Zatem
. Zatem
A) 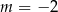 B)
B) 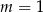 C)
C) 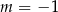 D)
D) 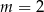
Na prostej o równaniu 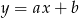 leżą punkty
leżą punkty 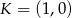 i
i 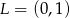 . Wynika stąd, że
. Wynika stąd, że
A) 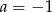 i
i 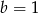 B)
B) 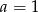 i
i 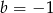 C)
C) 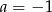 i
i 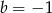 D)
D) 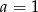 i
i 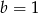
Na prostej o równaniu 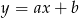 leżą punkty
leżą punkty 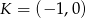 i
i 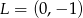 . Wynika stąd, że
. Wynika stąd, że
A) 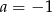 i
i 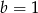 B)
B) 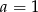 i
i 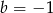 C)
C) 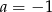 i
i 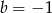 D)
D) 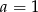 i
i 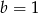
Dane są punkty 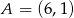 i
i 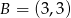 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 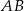 jest równy
jest równy
A) 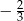 B)
B) 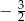 C)
C)  D)
D) 
W kartezjańskim układzie współrzędnych 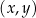 prosta o równaniu
prosta o równaniu 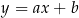 przechodzi przez punkty
przechodzi przez punkty 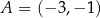 oraz
oraz 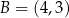 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 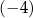 B)
B) 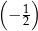 C) 2 D)
C) 2 D) 
W kartezjańskim układzie współrzędnych 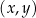 prosta o równaniu
prosta o równaniu 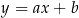 przechodzi przez punkty
przechodzi przez punkty 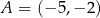 oraz
oraz 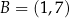 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A)  B)
B) 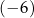 C)
C)  D)
D) 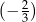
Wiadomo, że punkty 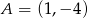 i
i 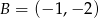 należą do prostej
należą do prostej 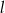 . Wówczas współczynnik kierunkowy prostej
. Wówczas współczynnik kierunkowy prostej 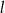 jest równy
jest równy
A) 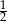 B) 1 C)
B) 1 C) 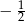 D)
D) 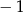
Współczynnik kierunkowy prostej, na której leżą punkty 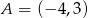 oraz
oraz 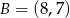 , jest równy
, jest równy
A) 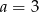 B)
B) 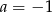 C)
C) 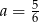 D)
D) 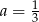
W układzie współrzędnych dane są dwa punkty 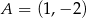 oraz
oraz 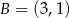 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 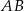 jest równy
jest równy
A) 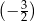 B)
B) 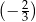 C)
C) 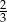 D)
D) 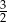
W układzie współrzędnych dane są dwa punkty 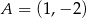 oraz
oraz 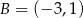 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 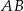 jest równy
jest równy
A) 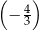 B)
B) 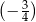 C)
C) 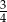 D)
D) 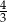
Współczynnik kierunkowy prostej, na której leżą punkty 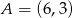 oraz
oraz 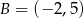 , jest równy
, jest równy
A) 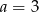 B)
B) 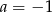 C)
C) 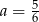 D)
D) 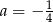
Prosta o równaniu 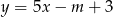 przechodzi przez punkt
przechodzi przez punkt 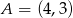 . Wtedy
. Wtedy
A) 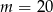 B)
B) 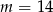 C)
C) 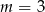 D)
D) 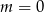
Prosta o równaniu 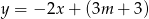 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 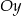 w punkcie
w punkcie 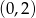 . Wtedy
. Wtedy
A) 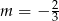 B)
B) 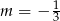 C)
C) 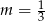 D)
D) 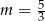
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 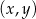 , dana jest prosta
, dana jest prosta 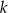 o równaniu
o równaniu 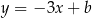 , przechodząca przez punkt
, przechodząca przez punkt 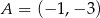 . Współczynnik
. Współczynnik 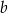 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 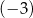 C)
C) 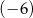 D)
D) 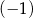
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 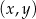 , dana jest prosta
, dana jest prosta 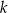 o równaniu
o równaniu 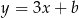 , przechodząca przez punkt
, przechodząca przez punkt 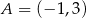 . Współczynnik
. Współczynnik 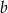 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 6 C) 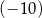 D) 8
D) 8
Punkt o współrzędnych 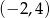 należy do prostej
należy do prostej 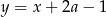 . Zatem
. Zatem
A) 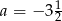 B)
B) 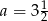 C)
C) 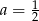 D)
D) 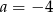
Prosta o równaniu 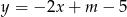 przechodzi przez punkt
przechodzi przez punkt 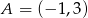 . Wtedy
. Wtedy
A) 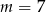 B)
B) 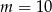 C)
C) 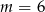 D)
D) 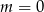
Prosta o równaniu 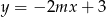 przechodzi przez punkt
przechodzi przez punkt 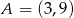 . Wtedy
. Wtedy
A) 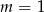 B)
B) 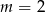 C)
C) 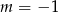 D)
D) 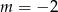
Prosta o równaniu 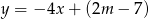 przechodzi przez punkt
przechodzi przez punkt 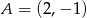 . Wtedy
. Wtedy
A) 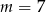 B)
B) 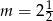 C)
C) 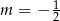 D)
D) 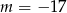
Prosta o równaniu 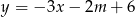 przechodzi przez punkt
przechodzi przez punkt 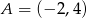 . Wtedy
. Wtedy
A) 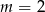 B)
B) 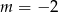 C)
C) 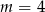 D)
D) 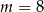
Prosta o równaniu 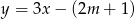 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 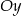 w punkcie
w punkcie 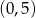 . Wtedy
. Wtedy
A) 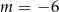 B)
B) 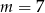 C)
C) 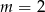 D)
D)