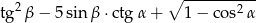Korzystając z własności trójkąta prostokątnego o kącie ostrym 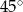 oblicz
oblicz 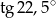 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Kąty, funkcje trygonometryczne
Oblicz sumę tangensów kątów ostrych trójkąta prostokątnego wiedząc że stosunek pola tego trójkąta do pola kwadratu, którego bokiem jest przeciwprostokątna danego trójkąta wynosi  .
.
Stosunek pola trójkąta prostokątnego do pola kwadratu, zbudowanego na przeciwprostokątnej tego trójkąta jest równy  . Oblicz sumę tangensów kątów ostrych tego trójkąta.
. Oblicz sumę tangensów kątów ostrych tego trójkąta.
Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa  .
.
- Uzasadnij, że spełniona jest nierówność
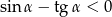 .
. - Dla
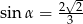 oblicz wartość wyrażenia
oblicz wartość wyrażenia 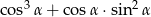 .
.
W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 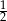 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy  . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Długości  i
i 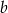 przyprostokątnych trójkąta prostokątnego spełniają równość
przyprostokątnych trójkąta prostokątnego spełniają równość
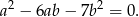
- Oblicz tangensy kątów ostrych tego trójkąta.
- Uzasadnij, że pole tego trójkąta jest równe
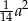 .
.
W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 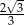 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Suma sinusów kątów ostrych w pewnym trójkącie prostokątnym wynosi 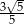 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Wyznacz wartości funkcji trygonometrycznych kątów ostrych trójkąta powstałego wskutek połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.
Dany jest trójkąt prostokątny równoramienny 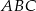 . Punkty
. Punkty 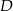 i
i 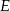 dzielą przeciwprostokątną
dzielą przeciwprostokątną 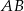 na trzy odcinki równej długości. Oblicz cosinus kąta
na trzy odcinki równej długości. Oblicz cosinus kąta 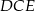 .
.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 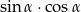 .
.
W trójkącie prostokątnym przyprostokątne mają długości 3 i 5, a jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 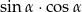 .
.
W trójkącie prostokątnym przyprostokątne mają długości 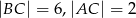 . Wyznacz wartość wyrażenia
. Wyznacz wartość wyrażenia 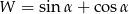 , gdzie
, gdzie  jest najmniejszym kątem ostrym tego trójkąta.
jest najmniejszym kątem ostrym tego trójkąta.
W trójkącie prostokątnym przyprostokątne mają długości 2 i 4, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 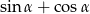 .
.
W trójkącie prostokątnym przyprostokątne mają długości 1 i 3, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 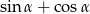 .
.
W trójkącie prostokątnym iloczyn sinusa jednego z kątów ostrych i tangensa drugiego kąta ostrego jest równy 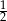 . Oblicz miary kątów ostrych tego trójkąta.
. Oblicz miary kątów ostrych tego trójkąta.
Dany jest trójkąt prostokątny 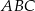 . Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta
. Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta 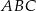 , który ma większą miarę.
, który ma większą miarę.
Dany jest trójkąt prostokątny 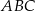 . Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta
. Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta 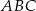 , który ma mniejszą miarę.
, który ma mniejszą miarę.
W trójkącie prostokątnym 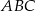 cosinus i tangens kąta przy wierzchołku
cosinus i tangens kąta przy wierzchołku 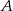 są równe. Oblicz sinus tego kąta.
są równe. Oblicz sinus tego kąta.
Sprawdź, czy trójkąt o bokach: 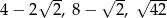 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Sprawdź, czy trójkąt o bokach: 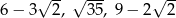 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
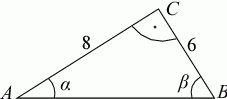
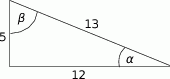
Na rysunku oznaczono kąty oraz podano długości boków trójkąta prostokątnego. Oblicz, które z wyrażeń ma większą wartość: 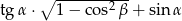 czy
czy 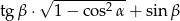 .
.
W trójkącie prostokątnym 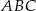 przyprostokątne mają długości
przyprostokątne mają długości 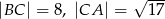 . Na boku
. Na boku 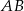 wybrano punkt
wybrano punkt 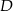 tak, że
tak, że 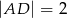 . Oblicz sinus kąta
. Oblicz sinus kąta 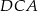 .
.
W trójkącie 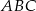 kąt przy wierzchołku
kąt przy wierzchołku 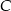 jest prosty. Trójkąt
jest prosty. Trójkąt 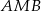 jest równoboczny. Oblicz miary kątów ostrych trójkąta
jest równoboczny. Oblicz miary kątów ostrych trójkąta 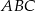 , jeśli pole trójkąta
, jeśli pole trójkąta 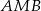 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 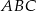 .
.
Oblicz tangens kąta ostrego utworzonego przez proste zawierające środkowe trójkąta prostokątnego równoramiennego poprowadzone na przyprostokątne.
W trójkącie prostokątnym 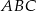 dwusieczna kąta prostego przecina przeciwprostokątną
dwusieczna kąta prostego przecina przeciwprostokątną 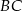 w punkcie
w punkcie 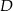 . Środek okręgu wpisanego w ten trójkąt dzieli odcinek
. Środek okręgu wpisanego w ten trójkąt dzieli odcinek 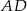 w stosunku
w stosunku 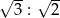 , licząc od punktu
, licząc od punktu 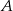 . Oblicz miary kątów ostrych trójkąta
. Oblicz miary kątów ostrych trójkąta 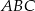 .
.
Oblicz sinusy kątów ostrych trójkąta prostokątnego, wiedząc, że stosunek długości promienia okręgu wpisanego do promienia okręgu opisanego na tym trójkącie jest równy 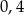 .
.
Wyznaczyć sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy  .
.
Wyznacz sinusy kątów ostrych trójkąta prostokątnego wiedząc, że stosunek promieni okręgów opisanego i wpisanego w ten trójkąt jest równy 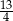 .
.
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia: