Dziewiąty wyraz ciągu arytmetycznego 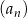 , określonego dla
, określonego dla 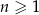 , jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę
Suma ośmiu początkowych wyrazów ciągu arytmetycznego 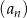 , określonego dla
, określonego dla 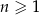 , jest równa 90, a suma
, jest równa 90, a suma 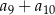 jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
Jedenasty wyraz ciągu arytmetycznego 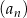 , określonego dla
, określonego dla 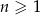 , jest równy
, jest równy 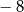 , a suma jego dziesięciu początkowych wyrazów jest równa
, a suma jego dziesięciu początkowych wyrazów jest równa 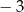 . Oblicz pierwszy wyraz i różnicę tego ciągu.
. Oblicz pierwszy wyraz i różnicę tego ciągu.
W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.
Pierwszy wyraz ciągu arytmetycznego jest równy 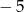 , a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
, a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
W ciągu arytmetycznym 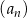 , określonym dla
, określonym dla 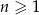 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 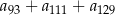 .
.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 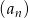 wyraża się wzorem
wyraża się wzorem 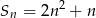 dla
dla 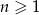 . Oblicz pierwszy wyraz ciągu i jego różnice.
. Oblicz pierwszy wyraz ciągu i jego różnice.
Suma 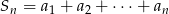 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 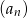 jest określona wzorem
jest określona wzorem 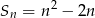 dla
dla 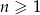 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Suma 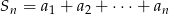 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 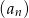 jest określona wzorem
jest określona wzorem 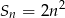 dla
dla 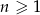 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Ile liczb trzeba wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny, którego suma jest równa 2008? Wyznacz różnicę tego ciągu.
Ile liczb trzeba wstawić między liczby 16 i 250, aby otrzymać ciąg arytmetyczny, którego suma jest równa 1995? Wyznacz różnicę tego ciągu.
Ciąg arytmetyczny 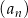 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 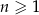 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 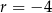 , a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: 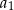 ,
, 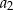 ,
, 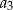 ,
, 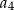 ,
, 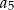 ,
, 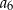 , jest równa 16.
, jest równa 16.
- Oblicz pierwszy wyraz tego ciągu.
- Oblicz liczbę
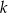 , dla której
, dla której 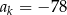 .
.
Ciąg arytmetyczny 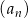 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 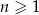 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 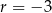 , a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu: 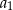 ,
, 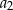 ,
, 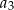 ,
, 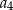 ,
, 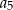 ,
, 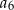 ,
, 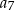 , jest równa
, jest równa 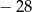 .
.
- Oblicz pierwszy wyraz tego ciągu.
- Wyznacz najmniejszą liczbę
 , dla której
, dla której 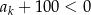 .
.
Dany jest ciąg arytmetyczny 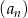 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 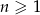 , w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
, w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Dany jest ciąg arytmetyczny 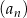 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 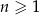 , w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
, w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
Dany jest ciąg 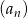 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 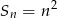 ,
, 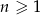 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Dany jest ciąg 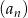 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 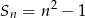 ,
, 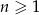 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
W skończonym ciągu arytmetycznym 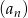 pierwszy wyraz
pierwszy wyraz 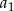 jest równy 7 oraz ostatni wyraz
jest równy 7 oraz ostatni wyraz 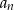 jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
W skończonym ciągu arytmetycznym 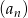 pierwszy wyraz
pierwszy wyraz 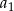 jest równy 9 oraz ostatni wyraz
jest równy 9 oraz ostatni wyraz 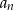 jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
Piąty wyraz ciągu arytmetycznego jest równy 26, a suma pięciu początkowych wyrazów tego ciągu jest równa 70. Oblicz pierwszy wyraz tego ciągu.
Dwudziesty wyraz ciągu arytmetycznego 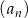 , określonego dla
, określonego dla 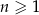 , jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
, jest równy 395, a suma jego dwudziestu początkowych wyrazów jest równa 8930. Oblicz pierwszy wyraz tego ciągu.
Dwunasty wyraz ciągu arytmetycznego 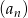 , określonego dla
, określonego dla 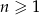 , jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
, jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
Siódmy wyraz ciągu arytmetycznego jest równy 34, a suma siedmiu początkowych wyrazów tego ciągu jest równa 56. Oblicz pierwszy wyraz tego ciągu.
Dany jest ciąg arytmetyczny 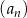 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 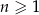 . Suma dwudziestu początkowych wyrazów tego ciągu jest równa
. Suma dwudziestu początkowych wyrazów tego ciągu jest równa 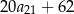 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 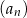 .
.
Dany jest ciąg arytmetyczny 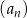 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 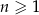 . Suma piętnastu początkowych wyrazów tego ciągu jest równa
. Suma piętnastu początkowych wyrazów tego ciągu jest równa 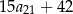 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 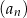 .
.
Trzeci wyraz ciągu arytmetycznego jest równy 4. Suma czterech pierwszych wyrazów tego ciągu jest równa 14. Oblicz 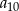 .
.
Czwarty wyraz ciągu arytmetycznego jest równy 8. Suma pięciu pierwszych wyrazów tego ciągu jest równa 15. Oblicz siódmy wyraz tego ciągu.
W ciągu arytmetycznym 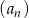 , określonym dla liczb naturalnych
, określonym dla liczb naturalnych 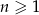 , wyraz szósty jest liczbą dwa razy większą od wyrazu piątego, a suma dziesięciu początkowych wyrazów tego ciągu jest równa
, wyraz szósty jest liczbą dwa razy większą od wyrazu piątego, a suma dziesięciu początkowych wyrazów tego ciągu jest równa 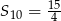 . Oblicz wyraz pierwszy oraz różnicę tego ciągu.
. Oblicz wyraz pierwszy oraz różnicę tego ciągu.
W ciągu arytmetycznym 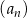 , określonym dla liczb naturalnych
, określonym dla liczb naturalnych 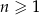 , wyraz piąty jest liczbą trzy razy mniejszą od wyrazu szóstego, a suma dwunastu początkowych wyrazów tego ciągu jest równa
, wyraz piąty jest liczbą trzy razy mniejszą od wyrazu szóstego, a suma dwunastu początkowych wyrazów tego ciągu jest równa 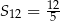 . Oblicz wyraz pierwszy oraz różnicę tego ciągu.
. Oblicz wyraz pierwszy oraz różnicę tego ciągu.
Dany jest ciąg 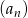 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 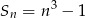 ,
, 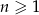 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 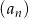 wyraża się wzorem
wyraża się wzorem 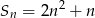 dla
dla 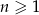 .
.
- Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych:
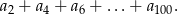
- Oblicz
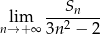
Dziesiąty wyraz ciągu arytmetycznego 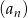 jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn
jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn 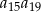 ma najmniejszą możliwą wartość.
ma najmniejszą możliwą wartość.
Dany jest ciąg arytmetyczny 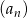 , gdzie
, gdzie 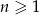 . Wiadomo, że dla każdego
. Wiadomo, że dla każdego 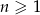 suma
suma  początkowych wyrazów
początkowych wyrazów 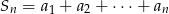 wyraża się wzorem:
wyraża się wzorem: 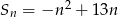 .
.
- Wyznacz wzór na
 –ty wyraz ciągu
–ty wyraz ciągu 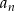 .
. - Oblicz
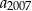 .
. - Wyznacz liczbę
 , dla której
, dla której 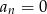 . .
. .
Suma szóstego i szesnastego wyrazu ciągu arytmetycznego 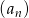 jest równa 5, a iloczyn wyrazu ósmego i dwunastego równy jest 3. Wyznacz wzór na wyraz ogólny ciągu
jest równa 5, a iloczyn wyrazu ósmego i dwunastego równy jest 3. Wyznacz wzór na wyraz ogólny ciągu 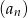 .
.
W ciągu arytmetycznym 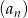 dany jest wyraz
dany jest wyraz 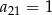 oraz suma 21 początkowych wyrazów
oraz suma 21 początkowych wyrazów 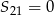 . Oblicz pierwszy wyraz oraz różnicę tego ciągu.
. Oblicz pierwszy wyraz oraz różnicę tego ciągu.
Suma czterdziestu początkowych wyrazów ciągu arytmetycznego 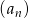 , określonego dla
, określonego dla 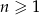 , jest równa 40. Ponadto
, jest równa 40. Ponadto 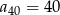 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 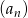 , określonego dla
, określonego dla 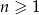 , jest równa 30. Ponadto
, jest równa 30. Ponadto 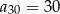 . Oblicz różnicę tego ciągu.
. Oblicz różnicę tego ciągu.

