Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Podzielność
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 5.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych, których cyfra tysięcy i cyfra setek należą do zbioru 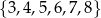 , a cyfra dziesiątek i cyfra jedności należą do zbioru
, a cyfra dziesiątek i cyfra jedności należą do zbioru 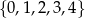 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
Ze zbioru liczb 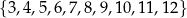 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 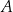 polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.
polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.
Niech  będzie ustaloną liczbą naturalną dodatnią. Ze zbioru
będzie ustaloną liczbą naturalną dodatnią. Ze zbioru 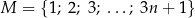 losujemy jednocześnie trzy liczby. Zdarzenie
losujemy jednocześnie trzy liczby. Zdarzenie 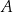 odpowiada jednoczesnemu wylosowaniu ze zbioru
odpowiada jednoczesnemu wylosowaniu ze zbioru 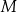 trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia
trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia 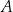 .
.
Z cyfr 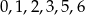 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Ze zbioru liczb 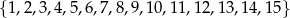 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 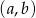 , gdzie
, gdzie  jest wynikiem pierwszego losowania,
jest wynikiem pierwszego losowania, 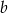 jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn
jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn 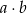 jest liczbą parzystą.
jest liczbą parzystą.
Losujemy jedną liczbę spośród liczb: 1, 2, 3,…, 1000. Oblicz prawdopodobieństwo wylosowania liczby podzielnej przez 4 lub przez 9.
Spośród liczb: 0, 1, 2, 3, 4, 5,…, 1000 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że liczba ta jest podzielna przez 4 lub 5.
Ze zbioru liczb trzycyfrowych mniejszych od 500 wybieramy losowo jedną liczbę. Jakie jest prawdopodobieństwo, że będzie to liczba podzielna przez 3 lub przez 5?
Ze zbioru liczb 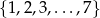 losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.
Ze zbioru liczb 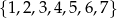 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 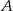 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 6.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 6.
Ze zbioru liczb 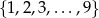 losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.
Ze zbioru liczb 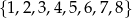 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 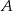 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 8.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 8.
W pudełku są cztery kartki, na których wypisano liczby 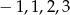 (na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę
(na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę 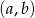 , gdzie
, gdzie  jest liczbą wylosowaną za pierwszym razem, zaś
jest liczbą wylosowaną za pierwszym razem, zaś 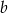 liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia
liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia
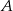 – iloczyn wylosowanych liczb jest liczbą pierwszą;
– iloczyn wylosowanych liczb jest liczbą pierwszą; 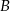 – różnica wylosowanych liczb jest liczbą parzystą.
– różnica wylosowanych liczb jest liczbą parzystą.
Ze zbioru liczb 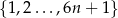 ,
, 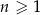 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 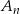 oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę
oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę 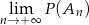 .
.
W urnie jest 15 kartek, ponumerowanych liczbami od 1 do 15. Wyciągamy 5 kartek bez zwracania. Jakie jest prawdopodobieństwo, że numer trzeciej kartki jest liczbą podzielną przez 3 i jednocześnie numer piątej kartki jest liczbą podzielną przez 5?
Ze zbioru liczb naturalnych pięciocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Ze zbioru liczb naturalnych czterocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 11.
Na sześciu jednakowych kartkach napisano liczby: 1, 10, 100, 1000, 10000, 100000. Z tych kartek losujemy kolejno bez zwracania trzy. Oblicz prawdopodobieństwo, że suma wylosowanych liczb tworzy liczbę podzielną przez cztery.
Ze zbioru cyfr 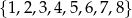 losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 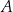 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia 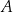 .
.
W dwóch pojemnikach znajdują się ponumerowane kule. W pierwszym pojemniku są kule z numerami: 1, 2, 3, 4, 5, w drugim z numerami: 4, 5, 6, 7, 8, 9. Losujemy po jednej kuli z każdego pojemnika i tworzymy liczbę dwucyfrową. Numer kuli wylosowanej z pierwszego pojemnika jest cyfrą dziesiątek, numer kuli wylosowanej z drugiego pojemnika jest cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że utworzona liczba jest podzielna przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 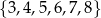 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 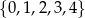 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 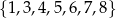 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 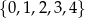 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 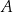 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 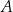 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 7 kul ponumerowanych kolejnymi liczbami od 2 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 9.
Ze zbioru 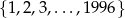 losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
- 6
- 4 lub 6
- 4 lub 6 lub 10
Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru liczb naturalnych dwucyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie większa od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie mniejsza od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych większych od 53 losujemy jedną liczbę. Niech 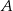 oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia 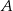 .
.
Ze zbioru liczb 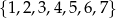 losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 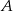 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
Ze zbioru liczb całkowitych spełniających nierówność 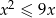 losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.
losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.
Ze zbioru liczb 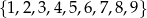 losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.
losujemy kolejno bez zwracania trzy liczby, zapisujemy je w kolejności losowania i tworzymy liczbę trzycyfrową w taki sposób, że pierwsza wylosowana liczba jest cyfrą setek, druga jest cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba trzycyfrowa jest podzielna przez 4. Wynik przedstaw w postaci ułamka nieskracalnego.

