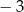Ramię końcowe kąta 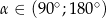 zawiera się w prostej
zawiera się w prostej 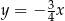 . Zatem
. Zatem
A) 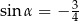 B)
B) 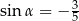 C)
C) 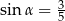 D)
D) 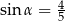
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Położenie względem osi
Dla jakiej wartości parametru 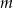 punkt przecięcia prostych
punkt przecięcia prostych 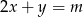 i
i 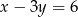 należy do osi
należy do osi 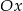 ?
?
A) dla 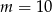 B) dla
B) dla 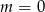 C) dla
C) dla 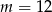 D) dla
D) dla 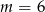
Proste o równaniach 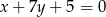 i
i 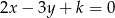 przecinają się na osi
przecinają się na osi 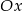 . Zatem parametr
. Zatem parametr 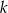 jest równy
jest równy
A) 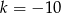 B)
B) 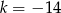 C)
C) 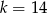 D)
D) 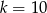
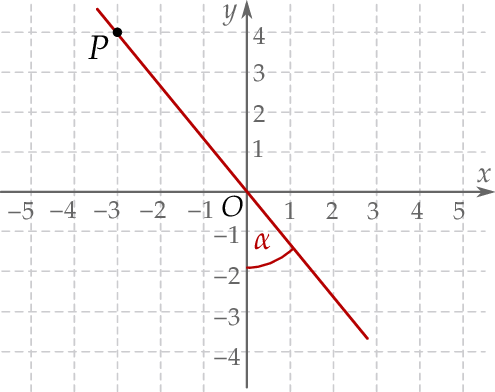
Punkty 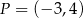 i
i 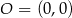 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 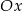 (zobacz rysunek).
(zobacz rysunek).
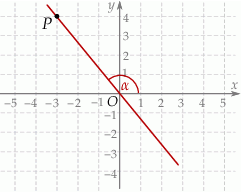
Wtedy tangens kąta  jest równy
jest równy
A) 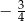 B)
B) 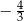 C)
C) 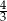 D)
D) 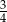
Punkty 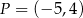 i
i 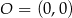 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi  (zobacz rysunek).
(zobacz rysunek).
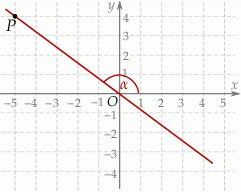
Wtedy tangens kąta  jest równy
jest równy
A)  B)
B)  C)
C) 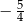 D)
D) 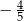
Które z danych równań opisuje prostą równoległą do osi 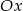 ?
?
A) 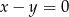 B)
B) 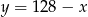 C)
C) 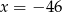 D)
D) 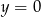
Które z danych równań opisuje prostą prostopadłą do osi 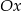 ?
?
A) 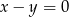 B)
B) 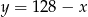 C)
C) 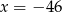 D)
D) 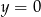
Punkty 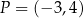 i
i  leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią  (zobacz rysunek).
(zobacz rysunek).
Wtedy tangens kąta  jest równy
jest równy
A) 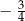 B)
B) 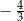 C)
C)  D)
D) 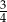
Na rysunkach A–F w kartezjańskim układzie współrzędnych 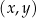 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 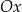 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 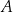 lub
lub 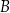 , lub
, lub 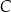 , lub
, lub 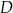 , lub
, lub 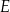 , lub
, lub 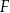 .
.
Na którym z rysunków zaznaczono kąt 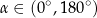 , spełniający warunek
, spełniający warunek 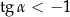 ?
?
Na rysunkach A–F w kartezjańskim układzie współrzędnych 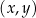 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 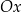 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 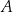 lub
lub  , lub
, lub  , lub
, lub  , lub
, lub  , lub
, lub 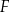 .
.
Na którym z rysunków zaznaczono kąt  , spełniający warunek
, spełniający warunek 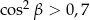 ?
?
Prosta 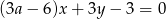 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 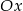 pod kątem
pod kątem 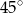 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 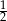 C) -1 D) 1
C) -1 D) 1
Prosta 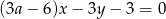 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 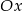 pod kątem
pod kątem 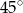 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 2 B) 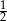 C) 3 D) 1
C) 3 D) 1
Prosta 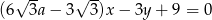 jest nachylona dodatniej półosi osi
jest nachylona dodatniej półosi osi 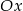 pod kątem
pod kątem 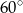 , gdy liczba
, gdy liczba  jest równa
jest równa
A) 1 B) 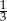 C) -1 D) 3
C) -1 D) 3
Prosta 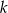 przecina oś
przecina oś 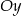 układu współrzędnych w punkcie
układu współrzędnych w punkcie 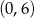 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 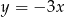 . Wówczas prosta
. Wówczas prosta 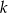 przecina oś
przecina oś 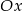 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 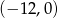 B)
B) 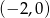 C)
C) 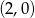 D)
D) 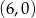
Prosta 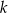 przecina oś
przecina oś 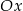 układu współrzędnych w punkcie
układu współrzędnych w punkcie 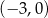 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 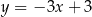 . Wówczas prosta
. Wówczas prosta 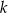 przecina oś
przecina oś 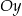 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 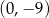 B)
B) 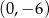 C)
C) 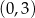 D)
D) 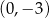
Prosta 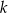 przecina oś
przecina oś 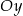 układu współrzędnych w punkcie
układu współrzędnych w punkcie 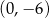 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 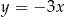 . Wówczas prosta
. Wówczas prosta 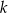 przecina oś
przecina oś 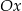 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 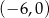 B)
B) 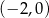 C)
C) 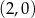 D)
D) 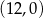
Na rysunkach A–F w kartezjańskim układzie współrzędnych 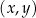 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 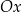 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 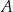 lub
lub 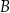 , lub
, lub 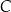 , lub
, lub 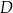 , lub
, lub 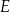 , lub
, lub 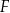 .
.
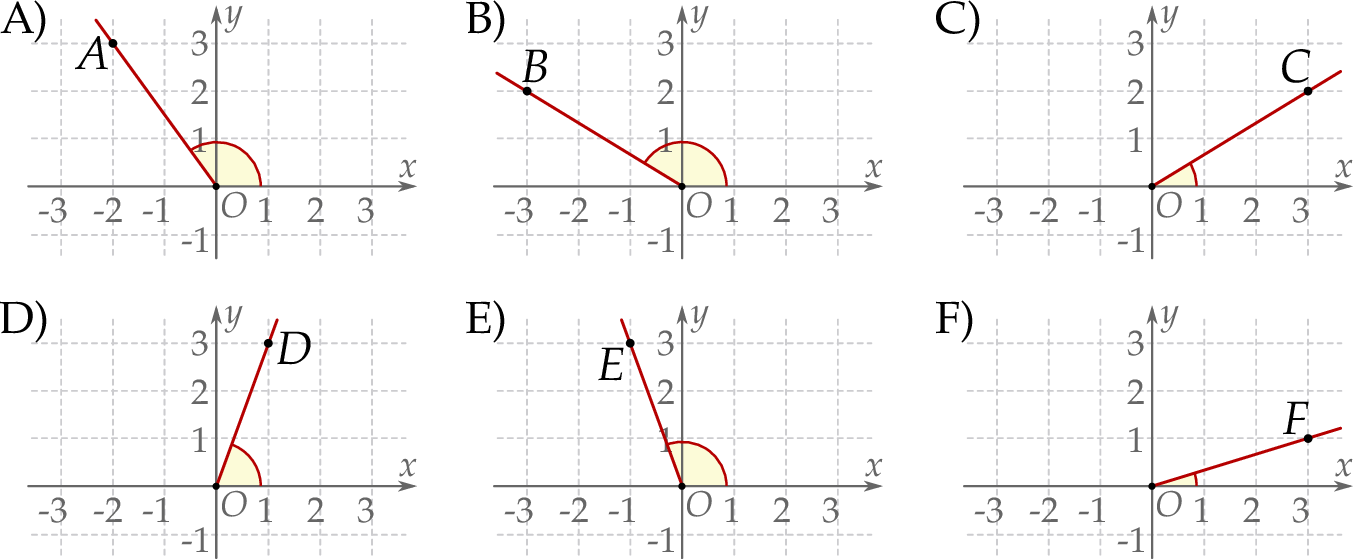
Kąt  , spełniający warunek
, spełniający warunek 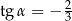 , jest zaznaczony na rysunku …
, jest zaznaczony na rysunku …
Na rysunkach A–F w kartezjańskim układzie współrzędnych 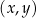 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 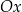 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 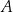 lub
lub 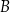 , lub
, lub 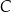 , lub
, lub 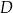 , lub
, lub 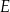 , lub
, lub 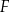 .
.
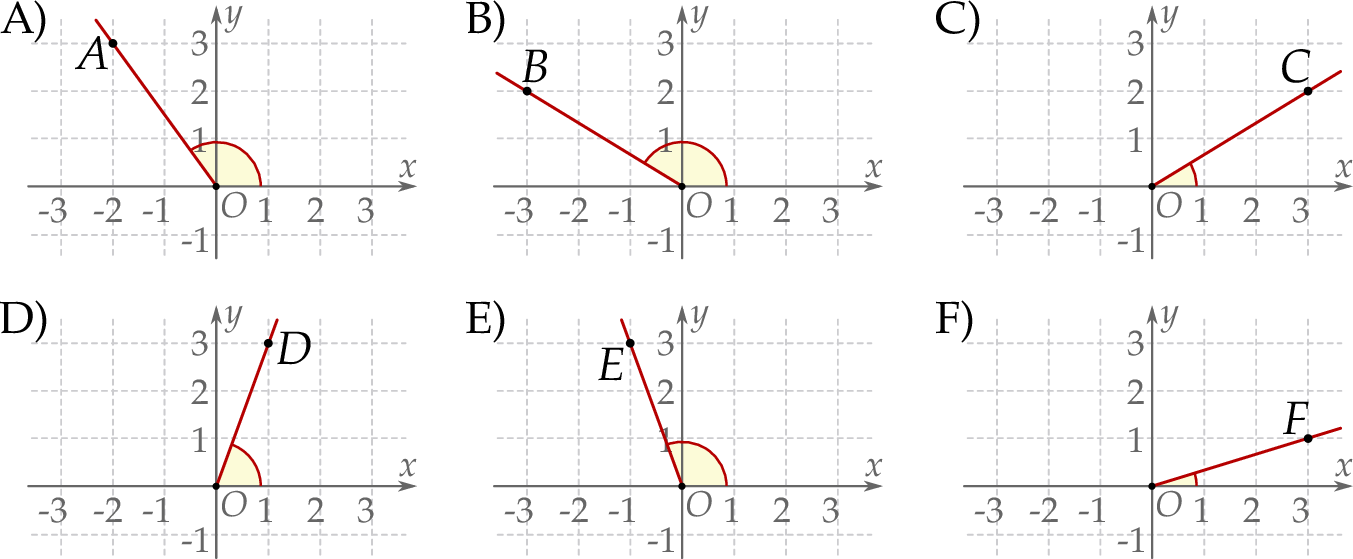
Na którym rysunku zaznaczono kąt  , spełniający warunek
, spełniający warunek 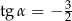 ?
?
Na rysunkach A–F w kartezjańskim układzie współrzędnych 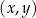 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 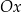 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 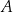 lub
lub 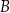 , lub
, lub 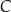 , lub
, lub 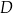 , lub
, lub 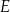 , lub
, lub 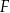 .
.
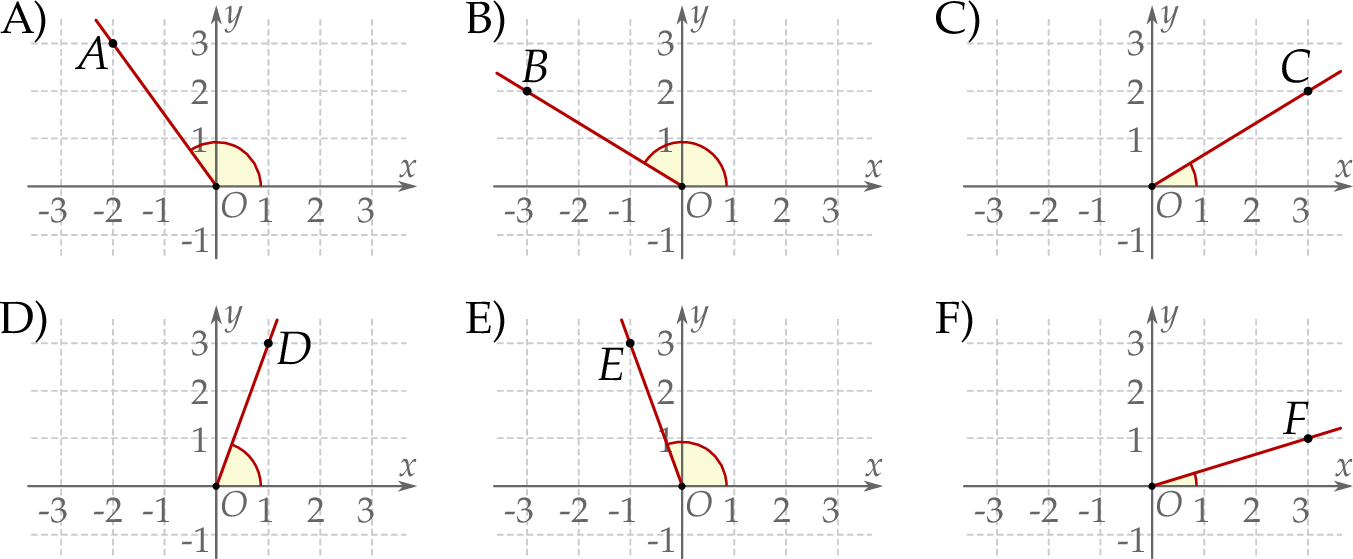
Na którym rysunku zaznaczono kąt 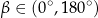 , spełniający warunek
, spełniający warunek 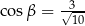 ?
?
Na rysunkach A–F w kartezjańskim układzie współrzędnych  zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 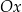 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 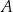 lub
lub 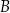 , lub
, lub 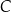 , lub
, lub  , lub
, lub  , lub
, lub  .
.
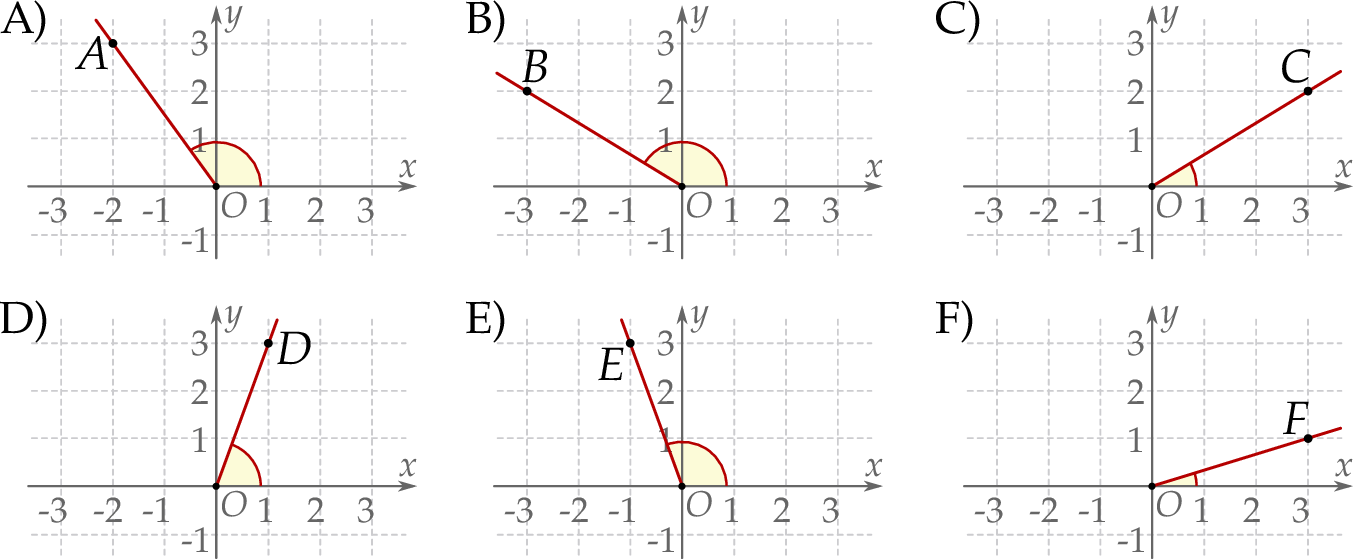
Kąt 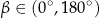 , spełniający warunek
, spełniający warunek 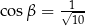 , jest zaznaczony na rysunku …
, jest zaznaczony na rysunku …
Prosta 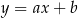 ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
ma z jedną osią układu współrzędnych dokładnie jeden punkt wspólny. Z drugą osią układu współrzędnych nie ma punktów wspólnych. Zatem prosta ta
A) przecina tylko oś  B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi  D) jest równoległa do osi
D) jest równoległa do osi 
Punkty wspólne prostej 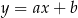 z osiami układu współrzędnych pokrywają się. Zatem prosta ta
z osiami układu współrzędnych pokrywają się. Zatem prosta ta
A) przecina tylko oś  B) przechodzi przez początek układu współrzędnych
B) przechodzi przez początek układu współrzędnych
C) jest równoległa do osi  D) jest równoległa do osi
D) jest równoległa do osi 
Jeżeli  jest kątem ostrym pod jakim przecinają się proste
jest kątem ostrym pod jakim przecinają się proste 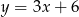 i
i 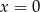 , to
, to
A) 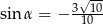 B)
B) 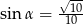 C)
C) 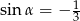 D)
D) 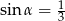
Prosta o równaniu 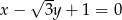 jest nachylona do osi
jest nachylona do osi 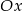 pod kątem
pod kątem  . Zatem
. Zatem
A) 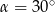 B)
B) 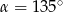 C)
C) 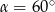 D)
D) 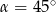
Prosta o równaniu 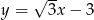 jest nachylona do osi
jest nachylona do osi 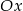 pod kątem
pod kątem
A) 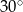 B)
B) 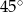 C)
C) 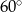 D)
D) 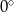
Prosta o równaniu 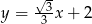 jest nachylona do osi
jest nachylona do osi  pod kątem
pod kątem  , takim, że
, takim, że
A) 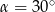 B)
B) 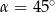 C)
C) 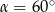 D)
D) 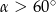
Prosta k o równaniu 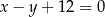 , tworzy z osią
, tworzy z osią 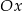 kąt o mierze równej
kąt o mierze równej
A) 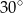 B)
B) 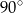 C)
C) 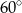 D)
D) 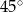
Prosta o równaniu 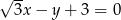 jest nachylona do osi
jest nachylona do osi 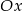 pod kątem
pod kątem  . Zatem
. Zatem
A) 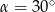 B)
B) 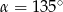 C)
C) 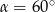 D)
D) 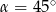
Prosta 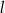 tworzy z osią
tworzy z osią 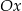 kąt
kąt 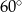 i przecina oś
i przecina oś 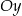 w punkcie
w punkcie 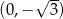 (zobacz rysunek).
(zobacz rysunek).
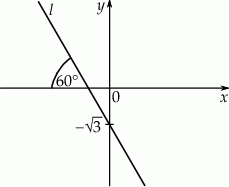
Prosta 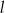 ma równanie
ma równanie
A) 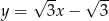 B)
B) 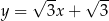 C)
C) 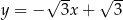 D)
D) 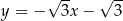
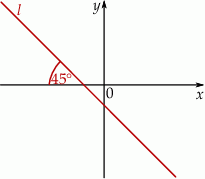
Prosta 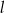 tworzy z osią
tworzy z osią 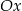 kąt ostry
kąt ostry 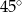 (zobacz rysunek) oraz przechodzi przez punkt o współrzędnych
(zobacz rysunek) oraz przechodzi przez punkt o współrzędnych 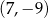 .
.
Prosta  ma równanie
ma równanie
A) 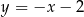 B)
B) 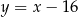 C)
C) 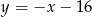 D)
D) 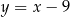
Obrazem prostej o równaniu 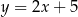 w symetrii osiowej względem osi
w symetrii osiowej względem osi 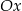 jest prosta o równaniu
jest prosta o równaniu
A) 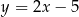 B)
B) 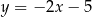 C)
C) 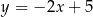 D)
D) 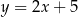
Na końcowym ramieniu kąta  (rysunek) leży punkt
(rysunek) leży punkt 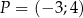 .
.
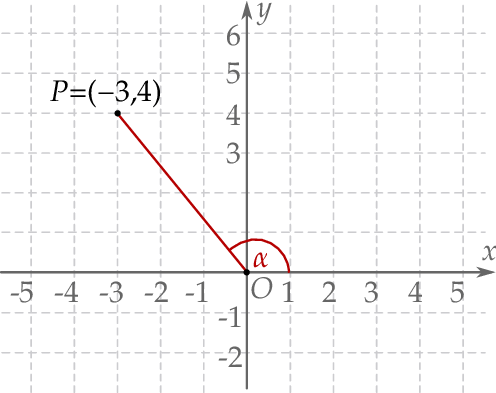
Wówczas
A) 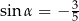 B)
B) 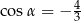 C)
C) 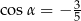 D)
D) 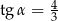
Punkt 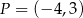 leży na końcowym ramieniu kąta
leży na końcowym ramieniu kąta  . Cosinus kąta
. Cosinus kąta  jest równy
jest równy
A)  B)
B) 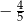 C)
C)  D)
D) 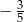
W kartezjańskim układzie współrzędnych 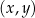 zaznaczono kąt o mierze
zaznaczono kąt o mierze  taki, że
taki, że 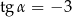 oraz
oraz 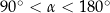 (zobacz rysunek).
(zobacz rysunek).
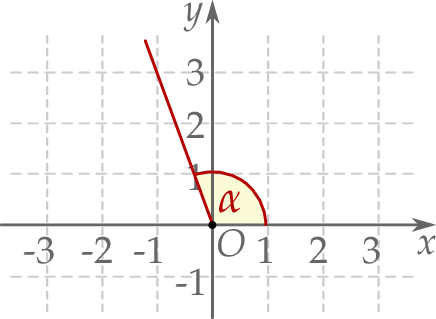
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Prawdziwa jest zależność
A) 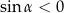 B)
B) 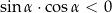 C)
C) 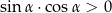
D) 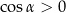 E)
E) 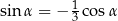 F)
F) 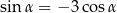
Prosta 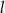 jest nachylona do osi
jest nachylona do osi 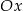 pod kątem
pod kątem 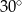 i przecina oś
i przecina oś 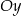 w punkcie
w punkcie 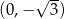 (zobacz rysunek).
(zobacz rysunek).
Prosta  ma równanie
ma równanie
A) 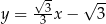 B)
B) 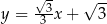 C)
C) 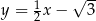 D)
D) 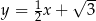
Prosta 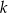 przechodzi przez punkt
przechodzi przez punkt 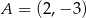 i jest nachylona do osi
i jest nachylona do osi 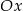 pod kątem
pod kątem 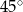 (zobacz rysunek).
(zobacz rysunek).
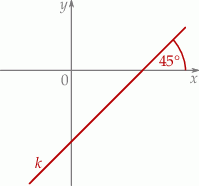
Prosta 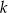 ma równanie
ma równanie
A) 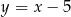 B)
B) 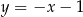 C)
C) 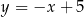 D)
D) 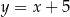
Prosta 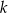 przechodzi przez punkt
przechodzi przez punkt 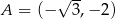 i jest nachylona do osi
i jest nachylona do osi 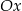 pod kątem
pod kątem 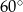 (zobacz rysunek).
(zobacz rysunek).
Prosta  ma równanie
ma równanie
A) 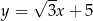 B)
B) 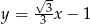 C)
C) 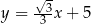 D)
D) 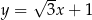
Prosta 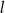 jest nachylona do osi
jest nachylona do osi 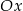 pod kątem
pod kątem 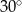 i przecina oś
i przecina oś 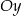 w punkcie
w punkcie 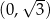 (zobacz rysunek).
(zobacz rysunek).
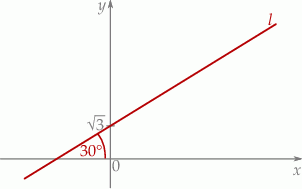
Prosta 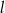 ma równanie
ma równanie
A) 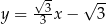 B)
B) 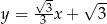 C)
C) 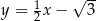 D)
D) 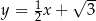
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
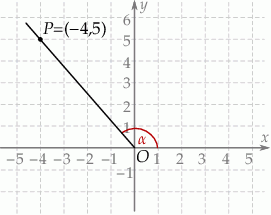
A) 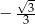 B)
B) 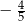 C)
C) 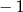 D)
D) 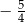
W kartezjańskim układzie współrzędnych  zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 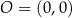 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 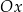 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 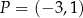 (zobacz rysunek).
(zobacz rysunek).
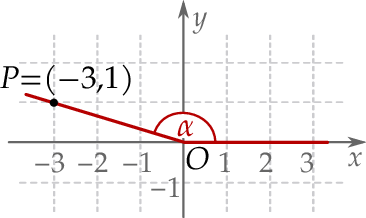
Tangens kąta  jest równy
jest równy
A) 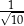 B)
B) 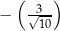 C)
C) 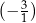 D)
D) 
W kartezjańskim układzie współrzędnych 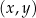 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 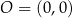 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 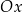 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 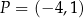 (zobacz rysunek).
(zobacz rysunek).
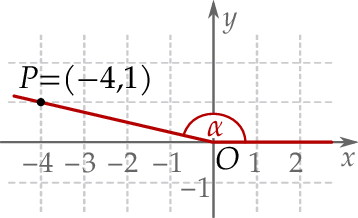
Tangens kąta  jest równy
jest równy
A) 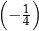 B)
B) 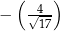 C)
C) 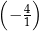 D)
D) 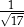
Na rysunku przedstawiona jest prosta 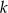 , przechodząca przez punkt
, przechodząca przez punkt 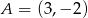 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 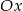 .
.
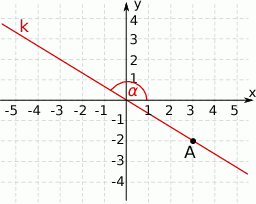
Zatem
A) 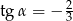 B)
B) 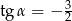 C)
C) 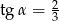 D)
D) 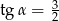
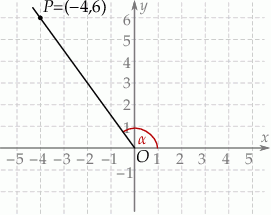
Na rysunku przedstawiona jest prosta, przechodząca przez punkty 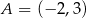 i
i 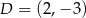 , oraz zaznaczony jest kąt
, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 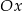 .
.
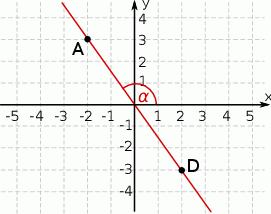
Zatem tangens kąta  jest równy
jest równy
A)  B)
B) 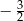 C)
C)  D)
D) 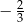
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 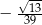 B)
B) 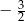 C)
C) 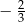 D)
D) 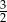
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
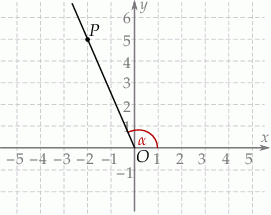
A) 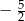 B)
B)  C)
C) 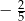 D)
D) 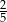
Na rysunku przedstawiona jest prosta 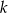 , przechodząca przez punkt
, przechodząca przez punkt 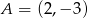 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi  .
.
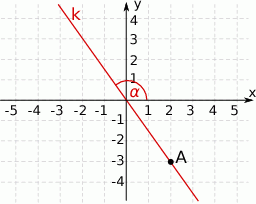
Zatem
A) 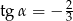 B)
B) 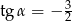 C)
C) 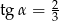 D)
D) 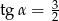
Prosta o równaniu 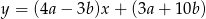 przecina oś
przecina oś 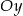 w punkcie
w punkcie 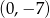 . Wtedy
. Wtedy
A) 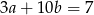 B)
B) 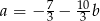 C)
C) 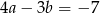 D)
D) 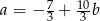
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
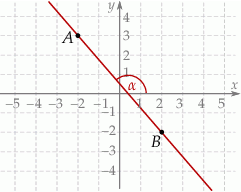
A)  B)
B) 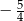 C)
C)  D)
D) 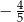
Na rysunku przedstawiona jest prosta 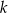 , przechodząca przez punkt
, przechodząca przez punkt 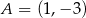 oraz przecinająca oś
oraz przecinająca oś 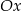 w punkcie
w punkcie 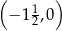 .
.
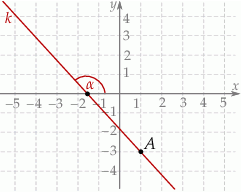
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 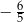 B)
B) 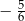 C)
C) 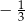 D)
D)