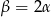Kąt  jest kątem ostrym w trójkącie prostokątnym, a
jest kątem ostrym w trójkącie prostokątnym, a 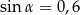 . Wówczas:
. Wówczas:
A) 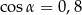 ,
, 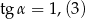 B)
B) 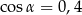 ,
, 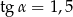
C) 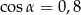 ,
, 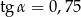 D)
D) 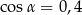 ,
, 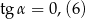
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny/Kąty, funkcje trygonometryczne/Dane z opisu
Dany jest trójkąt prostokątny o kątach ostrych  i
i 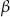 , w którym
, w którym 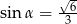 . Wtedy
. Wtedy
A) 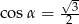 B)
B) 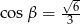 C)
C) 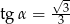 D)
D) 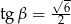
Przyprostokątne w trójkącie prostokątnym mają długości 1 i 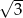 . Najmniejszy kąt w tym trójkącie ma miarę
. Najmniejszy kąt w tym trójkącie ma miarę
A) 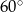 B)
B) 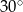 C)
C) 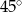 D)
D) 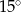
Przyprostokątne w trójkącie prostokątnym mają długości 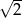 i
i 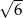 . Największy kąt ostry w tym trójkącie ma miarę
. Największy kąt ostry w tym trójkącie ma miarę
A) 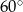 B)
B) 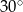 C)
C) 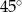 D)
D) 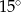
Jeżeli  i
i 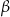 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 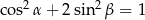 to
to
A) 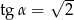 B)
B) 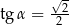 C)
C) 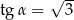 D)
D) 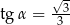
Jeżeli  i
i 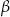 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 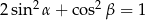 to
to
A) 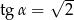 B)
B) 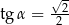 C)
C) 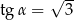 D)
D) 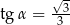
Jeśli przyprostokątne trójkąta prostokątnego są równe 6 i 3, a najmniejszy kąt ma miarę  , to wyrażenie
, to wyrażenie 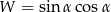 ma wartość
ma wartość
A) 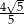 B)
B) 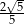 C)
C)  D)
D) 
W trójkącie prostokątnym o przyprostokątnych długości 1 i 2 kąty ostre są równe  i
i 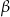 (
(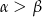 ). Wartość wyrażenia
). Wartość wyrażenia 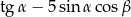 jest równe
jest równe
A) 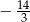 B) -2 C) 0 D)
B) -2 C) 0 D) 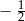
W trójkącie prostokątnym 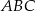 odcinek
odcinek 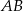 jest przeciwprostokątną i
jest przeciwprostokątną i 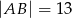 oraz
oraz 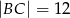 . Wówczas sinus kąta
. Wówczas sinus kąta 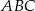 jest równy
jest równy
A) 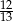 B)
B) 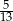 C)
C) 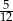 D)
D) 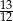
W trójkącie prostokątnym 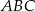 odcinek
odcinek 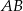 jest przeciwprostokątną i
jest przeciwprostokątną i 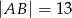 oraz
oraz 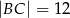 . Wówczas tangens kąta
. Wówczas tangens kąta 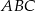 jest równy
jest równy
A) 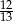 B)
B) 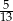 C)
C) 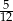 D)
D) 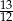
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 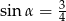 B)
B) 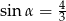 C)
C) 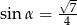 D)
D) 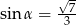
Przyprostokątna trójkąta prostokątnego ma długość 7, a przeciwprostokątna ma długość 9. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 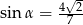 B)
B) 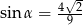 C)
C) 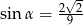 D)
D) 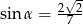
Przyprostokątna trójkąta prostokątnego ma długość 6, a przeciwprostokątna ma długość 8. Kąt  jest najmniejszym kątem tego trójkąta. Wówczas
jest najmniejszym kątem tego trójkąta. Wówczas
A) 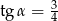 B)
B) 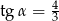 C)
C) 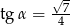 D)
D) 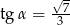
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 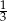 B) 3 C)
B) 3 C) 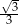 D)
D) 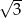
Jedna z przyprostokątnych trójkąta prostokątnego jest 5 razy krótsza od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 5 B) 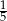 C)
C) 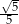 D)
D) 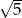
Przyprostokątne trójkąta prostokątnego mają długość 3 i 4. Wynika stąd, że tangens mniejszego z kątów ostrych jest równy
A)  B)
B)  C)
C) 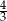 D)
D) 
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 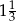 C)
C)  D)
D) 
Jedna z przyprostokątnych w trójkącie prostokątnym ma długość 3 cm, a przeciwprostokątna 4 cm. Najmniejszym kątem tego trójkąta jest  . Wartość wyrażenia
. Wartość wyrażenia 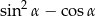 wynosi
wynosi
A) 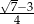 B)
B) 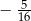 C)
C) 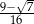 D) 1
D) 1
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 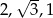 . Wtedy
. Wtedy
A) 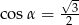 B)
B) 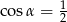 C)
C) 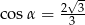 D)
D) 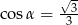
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 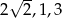 . Wtedy
. Wtedy
A) 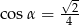 B)
B) 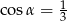 C)
C) 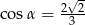 D)
D) 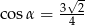
Niech  i
i 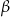 oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
A) 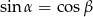 B)
B) 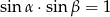 C)
C) 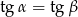 D)
D) 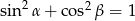
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 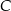 . Środkowa
. Środkowa 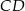 tworzy z przyprostokątną
tworzy z przyprostokątną 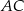 kąt
kąt 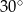 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 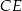 trójkąta ma miarę
trójkąta ma miarę
A) 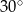 B)
B) 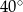 C)
C) 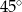 D)
D) 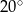
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 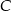 . Środkowa
. Środkowa 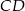 tworzy z przyprostokątną
tworzy z przyprostokątną 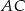 kąt
kąt 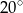 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 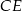 trójkąta ma miarę
trójkąta ma miarę
A) 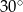 B)
B) 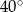 C)
C) 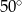 D)
D) 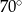
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 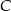 . Środkowa
. Środkowa 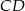 tworzy z przyprostokątną
tworzy z przyprostokątną 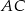 kąt
kąt 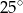 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 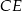 trójkąta ma miarę
trójkąta ma miarę
A) 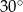 B)
B) 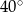 C)
C) 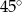 D)
D) 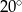
W trójkącie prostokątnym kąty ostre oznaczono  i
i 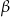 ,
, 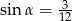 . Jaką miarę ma
. Jaką miarę ma 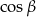 ?
?
A) 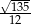 B)
B) 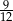 C)
C) 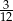 D)
D) 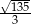
Przyprostokątne trójkąta prostokątnego mają długości 1 i 7. Sinus najmniejszego kąta tego trójkąta jest równy
A) 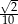 B)
B) 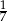 C)
C) 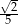 D)
D) 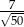
Przyprostokątne trójkąta prostokątnego mają długości 8 i 6. Sinus większego z kątów ostrych tego trójkąta jest równy
A)  B)
B)  C)
C)  D)
D) 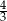
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 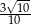 B)
B) 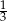 C)
C) 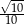 D)
D) 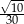
Przyprostokątne w trójkącie prostokątnym mają długości 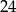 i
i 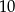 . Sinus najmniejszego kąta jest równy
. Sinus najmniejszego kąta jest równy
A) 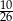 B)
B) 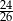 C)
C) 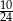 D)
D) 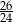
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 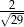 D)
D) 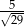
Przyprostokątne trójkąta prostokątnego mają długości 2 i 6. Sinus najmniejszego kąta tego trójkąta jest równy
A) 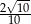 B)
B) 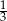 C)
C) 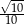 D)
D) 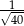
Przyprostokątna 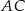 trójkąta prostokątnego
trójkąta prostokątnego 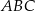 ma długość 6, a przeciwprostokątna
ma długość 6, a przeciwprostokątna 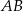 ma długość
ma długość 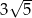 . Wtedy tangens kąta ostrego
. Wtedy tangens kąta ostrego 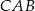 tego trójkąta jest równy
tego trójkąta jest równy
A) 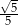 B)
B) 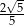 C)
C) 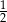 D) 2
D) 2
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 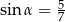 . Wówczas
. Wówczas
A) 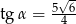 B)
B) 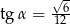 C)
C) 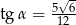 D)
D) 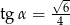
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 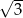 . Zatem
. Zatem
A) 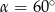 B)
B) 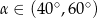 C)
C) 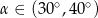 D)
D) 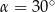
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 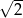 . Zatem
. Zatem
A) 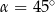 B)
B) 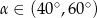 C)
C) 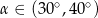 D)
D) 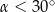
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 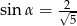 B)
B) 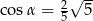 C)
C) 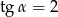 D)
D) 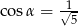
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
A) 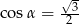 B)
B) 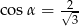 C)
C) 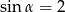 D)
D) 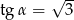
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 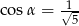 B)
B) 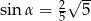 C)
C) 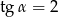 D)
D) 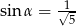
Dany jest trójkąt prostokątny 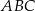 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 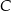 . Jeśli
. Jeśli 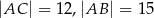 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C)  D)
D) 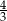
W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8 i jednej z przyprostokątnych 6. Tangens mniejszego kąta ostrego tego trójkąta jest równy
A)  B)
B) 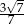 C)
C) 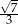 D)
D) 
Dany jest trójkąt prostokątny 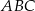 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 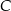 . Jeśli
. Jeśli 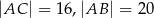 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C) 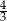 D)
D) 
Dany jest trójkąt prostokątny 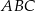 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 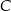 . Jeśli
. Jeśli 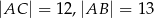 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A) 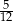 B)
B) 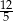 C)
C) 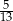 D)
D) 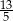
Jedna z przyprostokątnych trójkąta prostokątnego ma długość 15 cm, a przeciwprostokątna 17 cm. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 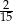 B)
B) 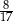 C)
C) 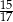 D)
D) 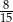
Trójkąt prostokątny ma boki długości 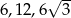 i kąty ostre
i kąty ostre 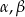 . Kąt
. Kąt 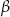 leży naprzeciw boku długości
leży naprzeciw boku długości 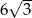 . Zatem
. Zatem
A) 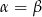 B)
B) 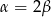 C)
C) 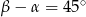 D)
D) 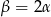
Trójkąt prostokątny ma boki długości 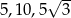 i kąty ostre
i kąty ostre 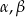 . Kąt
. Kąt 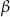 leży naprzeciw boku długości
leży naprzeciw boku długości 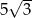 . Zatem
. Zatem
A) 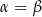 B)
B) 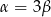 C)
C) 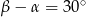 D)
D) 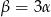
Trójkąt prostokątny ma boki długości 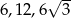 i kąty ostre
i kąty ostre 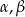 . Kąt
. Kąt 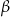 leży naprzeciw boku długości 6. Zatem
leży naprzeciw boku długości 6. Zatem
A) 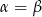 B)
B) 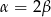 C)
C) 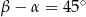 D)
D)