Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 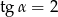 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 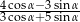 .
.
/Szkoła średnia/Funkcje/Trygonometryczna/Wartość wyrażenia
Oblicz wartość wyrażenia 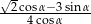 wiedząc, że
wiedząc, że 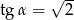 i
i 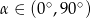 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 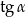 =3, oblicz wartość wyrażenia
=3, oblicz wartość wyrażenia 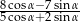 .
.
Kąt  jest ostry i
jest ostry i 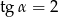 . Oblicz
. Oblicz 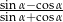 .
.
Oblicz wartość wyrażenia 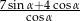 jeżeli
jeżeli  jest takim kątem ostrym, że
jest takim kątem ostrym, że 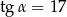 .
.
Oblicz wartość wyrażenia 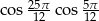 .
.
Wiedząc, że 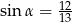 i
i 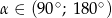 , oblicz
, oblicz 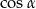 oraz
oraz 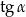 .
.
Wiedząc, że 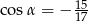 i
i 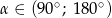 , oblicz
, oblicz 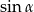 oraz
oraz 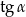 .
.
Oblicz 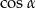 oraz
oraz 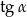 , jeżeli
, jeżeli 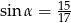 i
i 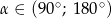 .
.
Kąt  jest ostry i
jest ostry i 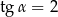 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 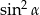 .
.
Wiedząc, że 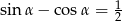 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 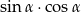 .
.
Wiedząc, że 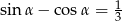 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 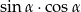 .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 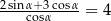 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 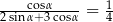 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 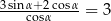 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Oblicz wartość wyrażenia 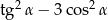 , jeżeli
, jeżeli 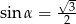 i
i  jest kątem ostrym.
jest kątem ostrym.
Kąt  jest ostry i
jest ostry i 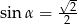 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 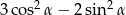 .
.
Kąt  jest ostry i
jest ostry i  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 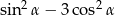 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 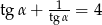 oblicz
oblicz 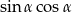 .
.
Kąt  jest ostry i
jest ostry i 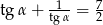 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 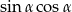 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 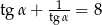 oblicz
oblicz 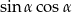 .
.
Porównaj liczby: 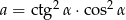 i
i 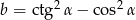 , jeżeli
, jeżeli 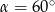 .
.
Posługując się wzorem 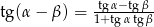 oblicz
oblicz 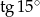 .
.
Kąt  jest ostry i
jest ostry i 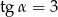 . Oblicz
. Oblicz 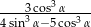 .
.
Kąt  jest ostry oraz
jest ostry oraz 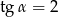 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 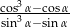 .
.
Kąt  jest ostry oraz
jest ostry oraz 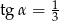 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 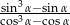 .
.
Kąt  jest kątem ostrym. Wiedząc, że
jest kątem ostrym. Wiedząc, że 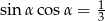 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 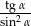 .
.
Kąt  jest ostry i
jest ostry i 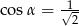 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 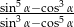 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 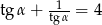 , oblicz
, oblicz 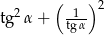 .
.
Wiedząc, że 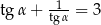 , oblicz
, oblicz 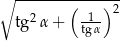 .
.
Oblicz 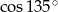 .
.
Oblicz 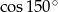 .
.
Kąt  jest ostry i
jest ostry i 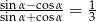 . Oblicz
. Oblicz 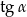 .
.
Kąt  spełnia warunek:
spełnia warunek: 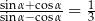 . Oblicz
. Oblicz 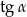 .
.
Wiedząc, że 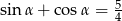 , oblicz
, oblicz 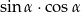 .
.
Dla pewnego kąta ostrego  spełniony jest warunek
spełniony jest warunek 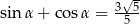 . Oblicz
. Oblicz 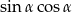 .
.
Wiedząc, że  , oblicz
, oblicz 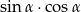 .
.
Kąt  jest ostry i
jest ostry i 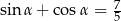 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 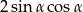 .
.
Kąt  jest ostry oraz
jest ostry oraz 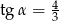 . Oblicz
. Oblicz 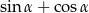 .
.
Kąt  jest ostry oraz
jest ostry oraz 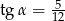 . Oblicz
. Oblicz 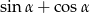 .
.
Kąt  jest ostry oraz
jest ostry oraz 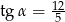 . Oblicz
. Oblicz 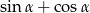 .
.
Oblicz 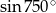 .
.
Oblicz 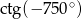 .
.
Oblicz 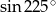 .
.
Oblicz 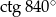 .
.
Oblicz 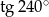 .
.
Oblicz 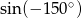 .
.
Oblicz 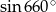 .
.
Oblicz 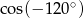 .
.
Oblicz 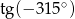 .
.

