Dany jest ciąg geometryczny 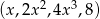 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 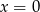 B)
B) 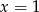 C)
C) 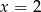 D)
D) 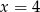
/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny/Z parametrem
Dany jest ciąg geometryczny 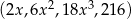 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 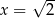 B)
B) 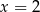 C)
C) 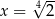 D)
D) 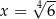
Dany jest ciąg geometryczny 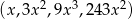 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 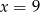 B)
B) 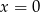 C)
C) 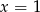 D)
D) 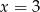
Ciąg 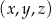 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że 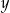 jest równe
jest równe
A) 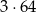 B)
B) 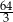 C) 4 D) 3
C) 4 D) 3
Ciąg 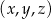 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że 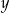 jest równe
jest równe
A) 81 B) 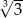 C) 9 D) 3
C) 9 D) 3
Ciąg 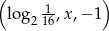 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 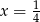 B)
B) 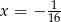 C)
C) 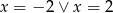 D)
D) 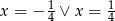
Ciąg 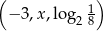 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 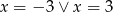 B)
B) 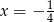 C)
C) 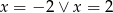 D)
D) 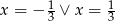
Ciąg 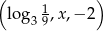 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 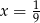 B)
B) 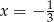 C)
C) 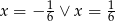 D)
D) 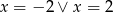
Trzywyrazowy ciąg 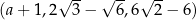 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 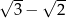 B)
B) 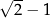 C)
C) 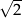 D)
D) 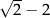
Liczby 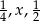 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 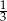 B)
B)  C)
C) 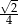 D)
D) 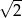
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 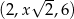 . Wówczas
. Wówczas
A) 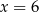 B)
B) 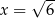 C)
C) 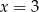 D)
D) 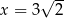
Trzywyrazowy ciąg 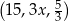 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 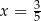 B)
B) 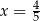 C)
C) 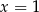 D)
D) 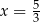
Trójwyrazowy ciąg 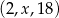 jest rosnącym ciągiem geometrycznym. Wtedy
jest rosnącym ciągiem geometrycznym. Wtedy
A) 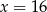 B)
B) 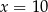 C)
C) 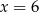 D)
D) 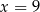
Liczby 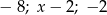 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  może być równa
może być równa
A) 4 B) 6 C) 7 D) 8
Trzywyrazowy ciąg 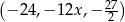 jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
A) 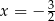 B)
B) 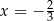 C)
C) 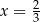 D)
D) 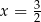
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 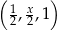 . Wówczas
. Wówczas
A) 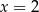 B)
B) 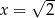 C)
C) 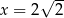 D)
D) 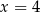
Liczby 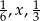 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 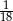 B)
B) 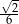 C)
C) 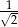 D)
D) 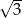
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 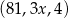 . Stąd wynika, że
. Stąd wynika, że
A) 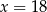 B)
B) 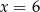 C)
C) 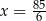 D)
D) 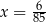
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 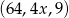 . Stąd wynika, że
. Stąd wynika, że
A) 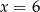 B)
B) 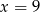 C)
C) 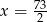 D)
D) 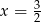
Liczby 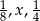 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 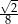 B)
B) 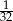 C)
C) 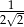 D)
D) 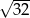
Liczby 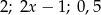 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
A) 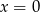 B)
B) 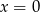 lub
lub 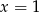 C)
C) 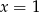 D)
D) 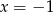
Ciąg 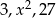 jest ciągiem geometrycznym, gdy
jest ciągiem geometrycznym, gdy
A) tylko 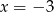 B) tylko
B) tylko 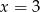 C)
C) 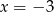 lub
lub 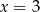 D)
D) 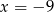 lub
lub 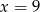
Ciąg 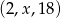 jest ciągiem geometrycznym tylko wtedy, gdy
jest ciągiem geometrycznym tylko wtedy, gdy
A) 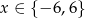 B)
B) 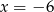 C)
C) 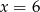 D)
D) 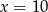
Jeżeli liczby 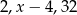 tworzą rosnący ciąg geometryczny, to
tworzą rosnący ciąg geometryczny, to
A) 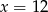 B)
B) 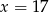 C)
C) 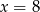 D)
D) 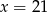
Pięciowyrazowy ciąg 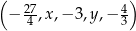 jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
jest geometryczny i nie wszystkie jego wyrazy są ujemne. Iloczyn wszystkich wyrazów tego ciągu jest równy
A) 81 B) 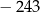 C)
C) 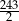 D)
D) 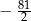
Czterowyrazowy ciąg 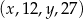 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 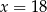 B)
B) 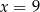 C)
C) 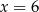 D)
D) 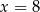
Wiadomo, że liczba 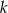 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 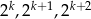 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 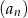 , gdzie
, gdzie 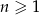 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 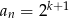 B)
B) 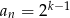 C)
C) 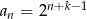 D)
D) 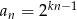
Wiadomo, że liczba 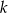 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 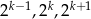 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 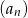 , gdzie
, gdzie 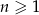 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 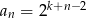 B)
B) 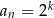 C)
C) 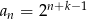 D)
D) 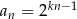
Wiadomo, że liczba 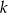 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 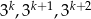 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 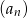 , gdzie
, gdzie 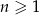 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 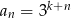 B)
B) 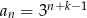 C)
C) 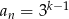 D)
D) 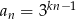
Liczby 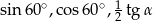 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa
A) 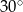 B)
B) 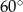 C)
C) 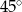 D)
D) 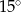
Liczby 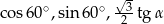 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa
A) 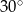 B)
B) 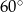 C)
C) 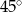 D)
D) 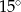
Liczby 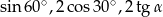 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa
A) 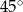 B)
B) 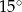 C)
C) 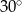 D)
D) 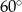
Czterowyrazowy ciąg 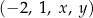 jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
A) 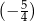 B)
B) 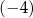 C)
C) 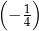 D)
D) 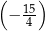
Liczby 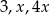 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 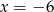 B)
B) 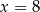 C)
C) 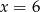 D)
D) 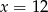
Liczby 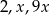 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 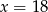 B)
B) 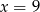 C)
C) 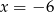 D)
D) 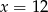
Dany jest rosnący ciąg geometryczny 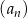 , określony dla liczb naturalnych
, określony dla liczb naturalnych 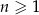 , o wyrazach dodatnich. Jeśli
, o wyrazach dodatnich. Jeśli 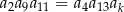 , to
, to 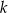 jest równe
jest równe
A) 8 B) 7 C) 6 D) 5
Cztery liczby dodatnie 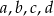 w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby
w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby 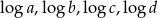 (w podanej kolejności) tworzą
(w podanej kolejności) tworzą
A) ciąg geometryczny o ilorazie 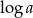
B) ciąg geometryczny o ilorazie 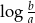
C) ciąg arytmetyczny o różnicy 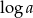
D) ciąg arytmetyczny o różnicy 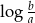
Cztery liczby dodatnie 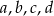 w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby
w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby 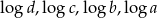 (w podanej kolejności) tworzą
(w podanej kolejności) tworzą
A) ciąg geometryczny o ilorazie 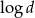
B) ciąg arytmetyczny o różnicy 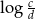
C) ciąg arytmetyczny o różnicy 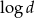
D) ciąg arytmetyczny o różnicy 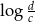
Masa 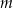 leku
leku 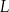 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
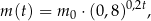
gdzie:
-
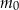 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 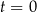 dawki leku,
dawki leku, -
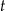 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 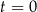 zażycia leku.
zażycia leku.
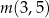 ,
, 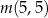 ,
, 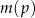 w podanej kolejności tworzą ciąg geometryczny. Liczba
w podanej kolejności tworzą ciąg geometryczny. Liczba 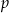 jest równa
jest równa A) 8,5 B) 9 C) 6 D) 7,5
Ciąg 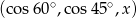 jest geometryczny. Wobec tego
jest geometryczny. Wobec tego
A) 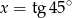 B)
B) 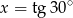 C)
C) 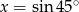 D)
D) 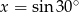
Ciąg 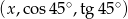 jest geometryczny. Wobec tego
jest geometryczny. Wobec tego
A) 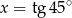 B)
B) 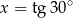 C)
C) 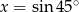 D)
D) 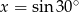
Ciąg 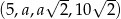 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 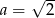 B)
B) 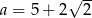 C)
C) 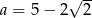 D)
D) 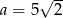
Liczby 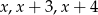 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 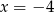 B)
B) 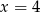 C)
C) 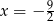 D)
D) 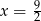
Liczby 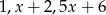 są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba
są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba  spełnia warunek
spełnia warunek
A) 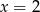 B)
B) 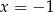 C)
C) 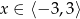 D)
D) 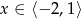
Ciąg 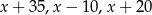 jest geometryczny. Stąd wynika, że
jest geometryczny. Stąd wynika, że
A) 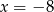 B)
B) 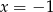 C)
C) 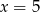 D)
D) 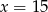
Ciąg 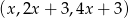 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 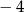 B) 1 C) 0 D)
B) 1 C) 0 D) 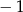
Dla pewnej liczby  ciąg
ciąg 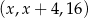 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 8 B) 4 C) 2 D) 0
Ciąg 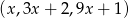 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 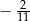 B)
B) 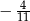 C)
C) 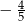 D)
D) 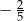
Liczby 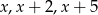 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 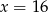 B)
B) 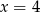 C)
C) 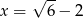 D)
D) 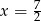
Dla pewnej liczby  ciąg
ciąg 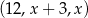 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 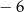 B) 9 C) 6 D) 3
B) 9 C) 6 D) 3
Liczby 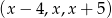 tworzą ciąg geometryczny dla
tworzą ciąg geometryczny dla
A) 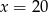 B)
B) 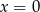 C)
C) 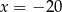 D)
D) 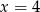
Liczby 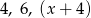 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba  jest równa:
jest równa:
A) 9 B) 10 C) 13 D) 5
Trzywyrazowy ciąg 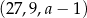 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 0 C) 4 D) 2
Dany jest trzywyrazowy ciąg geometryczny 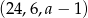 . Stąd wynika, że
. Stąd wynika, że
A) 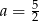 B)
B) 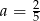 C)
C) 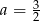 D)
D) 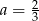
Dany jest ciąg liczbowy 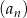 , w którym
, w którym 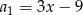 ,
, 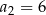 ,
, 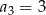 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem geometrycznym?
dany ciąg jest ciągiem geometrycznym?
A) 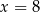 B)
B) 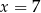 C)
C) 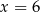 D)
D) 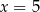
Trzywyrazowy ciąg 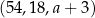 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 6 C) 4 D) 2
Ciąg 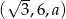 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 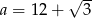 B)
B) 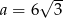 C)
C) 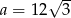 D)
D) 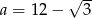
Liczby 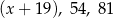 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
A) 62 B) 36 C) 35 D) 17
Liczby 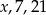 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 1 B)  C)
C) 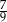 D)
D) 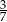
Liczby 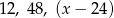 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
A) 192 B) 216 C) 60 D) 24
Ciąg 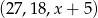 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 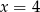 B)
B) 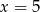 C)
C) 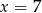 D)
D) 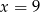
Liczby: 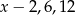 , w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 0 B) 2 C) 3 D) 5
Liczby 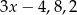 w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
A) 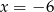 B)
B) 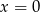 C)
C) 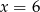 D)
D) 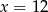
Trzywyrazowy ciąg 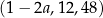 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 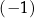 B) 3 C) 4 D) 12,5
B) 3 C) 4 D) 12,5
Ciąg 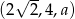 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 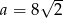 B)
B) 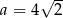 C)
C) 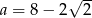 D)
D) 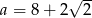
Trzywyrazowy ciąg 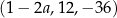 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 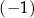 B) 5 C) 4 D) 2,5
B) 5 C) 4 D) 2,5
Ciąg 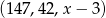 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 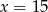 B)
B) 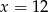 C)
C) 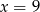 D)
D) 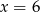
Liczby 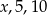 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 2,5 B) 5 C) 10 D) 0
Liczby 9,-3 i 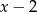 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) 1 B) -1,5 C) 5 D) 3
Liczby -8,4 i 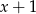 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) -3 B) -1,5 C) 1 D) 15
Trójwyrazowy ciąg 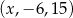 jest ciągiem geometrycznym. Wtedy
jest ciągiem geometrycznym. Wtedy
A) 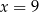 B)
B) 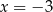 C)
C) 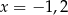 D)
D) 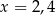
Dany jest ciąg geometryczny
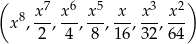
o wyrazach dodatnich. Wtedy
A) 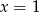 B)
B) 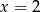 C)
C) 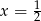 D)
D) 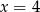
Liczby 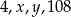 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 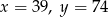 B)
B) 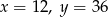 C)
C) 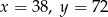 D)
D) 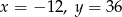
Liczby 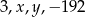 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 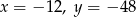 B)
B) 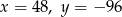 C)
C) 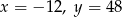 D)
D) 

