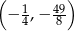Wykresem funkcji kwadratowej 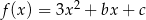 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 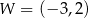 . Wzór tej funkcji w postaci kanonicznej to
. Wzór tej funkcji w postaci kanonicznej to
A) 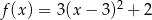 B)
B) 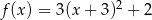
C) 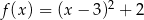 D)
D) 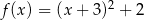
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Parabola/Wierzchołek
Wykresem funkcji kwadratowej 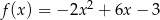 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 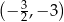 B)
B) 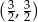 C)
C) 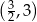 D)
D) 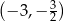
Punkt 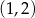 jest wierzchołkiem paraboli o równaniu
jest wierzchołkiem paraboli o równaniu
A) 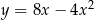 B)
B) 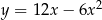 C)
C) 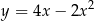 D)
D) 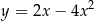
Wykresem funkcji kwadratowej 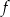 określonej wzorem
określonej wzorem 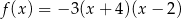 jest parabola o wierzchołku
jest parabola o wierzchołku 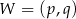 . Współrzędne wierzchołka
. Współrzędne wierzchołka 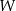 spełniają warunki
spełniają warunki
A) 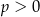 i
i 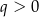 B)
B) 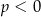 i
i 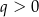 C)
C) 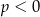 i
i 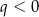 D)
D) 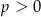 i
i 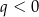
Wykresem funkcji kwadratowej 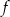 określonej wzorem
określonej wzorem 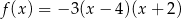 jest parabola o wierzchołku
jest parabola o wierzchołku 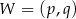 . Współrzędne wierzchołka
. Współrzędne wierzchołka 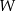 spełniają warunki
spełniają warunki
A) 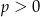 i
i 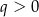 B)
B) 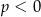 i
i 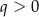 C)
C) 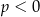 i
i 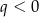 D)
D) 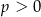 i
i 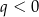
Wierzchołek paraboli będącej wykresem funkcji 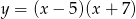 ma współrzędne
ma współrzędne
A) 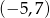 B)
B) 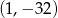 C)
C) 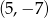 D)
D) 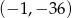
Współrzędne wierzchołka paraboli będącej wykresem funkcji 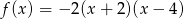 są równe
są równe
A) 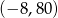 B)
B) 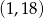 C)
C) 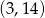 D)
D) 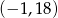
Współrzędne wierzchołka paraboli będącej wykresem funkcji 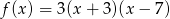 są równe
są równe
A) 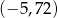 B)
B) 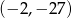 C)
C) 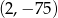 D)
D) 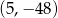
Wierzchołek paraboli będącej wykresem funkcji 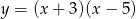 ma współrzędne
ma współrzędne
A) 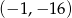 B)
B) 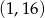 C)
C) 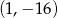 D)
D) 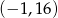
Współrzędne wierzchołka paraboli będącej wykresem funkcji 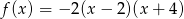 są równe
są równe
A) 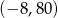 B)
B) 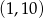 C)
C) 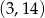 D)
D) 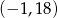
Wierzchołek paraboli będącej wykresem funkcji 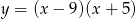 ma współrzędne
ma współrzędne
A) 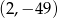 B)
B) 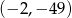 C)
C) 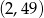 D)
D) 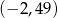
Wierzchołek paraboli o równaniu 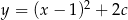 leży na prostej o równaniu
leży na prostej o równaniu 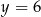 . Wtedy
. Wtedy
A) 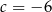 B)
B) 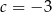 C)
C) 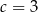 D)
D) 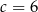
Wierzchołek paraboli o równaniu 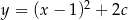 leży na prostej o równaniu
leży na prostej o równaniu 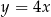 . Wtedy
. Wtedy
A) 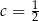 B)
B) 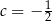 C)
C) 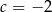 D)
D) 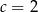
Wierzchołek paraboli o równaniu 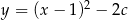 leży na prostej o równaniu
leży na prostej o równaniu 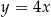 . Wtedy
. Wtedy
A) 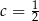 B)
B) 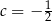 C)
C) 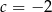 D)
D) 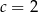
Jeśli wiadomo, że wierzchołek funkcji 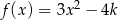 należy do prostej
należy do prostej 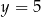 , to wartość liczbowa współczynnika
, to wartość liczbowa współczynnika 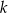 jest równa
jest równa
A) 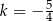 B)
B) 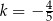 C)
C) 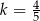 D)
D) 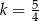
Wierzchołek paraboli o równaniu 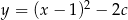 leży na prostej o równaniu
leży na prostej o równaniu 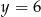 . Wtedy
. Wtedy
A) 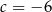 B)
B) 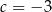 C)
C) 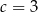 D)
D) 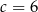
Wykresem funkcji kwadratowej 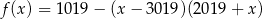 jest parabola, której wierzchołek leży na prostej
jest parabola, której wierzchołek leży na prostej
A) 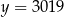 B)
B) 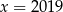 C)
C) 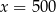 D)
D) 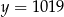
Wierzchołek paraboli o równaniu 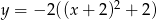 ma współrzędne
ma współrzędne
A) 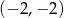 B)
B) 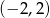 C)
C) 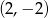 D)
D) 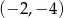
Wierzchołek paraboli o równaniu 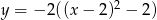 ma współrzędne
ma współrzędne
A) 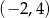 B)
B) 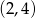 C)
C) 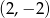 D)
D) 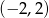
Suma współrzędnych wierzchołka paraboli 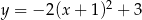 jest równa
jest równa
A) 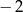 B) 2 C)
B) 2 C) 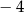 D) 4
D) 4
Funkcja kwadratowa 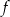 jest określona wzorem
jest określona wzorem 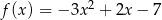 . Wykresem funkcji
. Wykresem funkcji 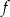 jest parabola, której wierzchołek leży na prostej o równaniu
jest parabola, której wierzchołek leży na prostej o równaniu
A) 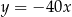 B)
B) 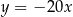 C)
C) 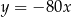 D)
D) 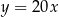
Wierzchołek paraboli o równaniu 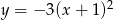 ma współrzędne
ma współrzędne
A) 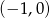 B)
B) 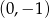 C)
C) 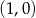 D)
D) 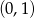
Funkcja kwadratowa 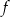 jest określona wzorem
jest określona wzorem 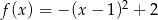 . Wykresem funkcji
. Wykresem funkcji 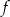 jest parabola, której wierzchołek ma współrzędne
jest parabola, której wierzchołek ma współrzędne
A) 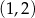 B)
B) 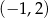 C)
C) 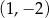 D)
D) 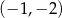
Wykresem funkcji kwadratowej 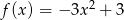 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 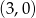 B)
B) 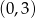 C)
C) 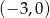 D)
D) 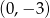
Wierzchołek paraboli o równaniu 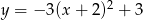 ma współrzędne
ma współrzędne
A) 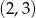 B)
B) 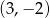 C)
C) 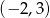 D)
D) 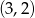
Wierzchołek paraboli o równaniu 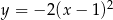 ma współrzędne
ma współrzędne
A) 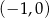 B)
B) 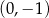 C)
C) 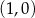 D)
D) 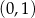
Wykresem funkcji kwadratowej 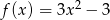 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 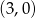 B)
B) 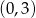 C)
C) 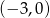 D)
D) 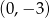
Wierzchołkiem paraboli o równaniu 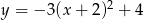 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 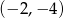 B)
B) 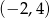 C)
C) 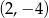 D)
D) 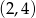
Wykresem funkcji kwadratowej 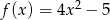 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie
A) 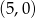 B)
B) 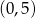 C)
C) 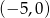 D)
D) 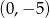
Funkcja kwadratowa 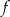 jest określona wzorem
jest określona wzorem 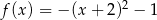 . Wykresem funkcji
. Wykresem funkcji 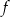 jest parabola, której wierzchołek ma współrzędne
jest parabola, której wierzchołek ma współrzędne
A) 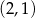 B)
B) 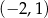 C)
C) 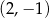 D)
D) 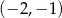
Wierzchołek paraboli o równaniu 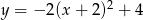 ma współrzędne
ma współrzędne
A) 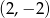 B)
B) 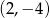 C)
C) 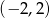 D)
D) 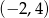
Wierzchołkiem paraboli o równaniu 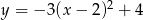 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 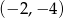 B)
B) 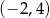 C)
C) 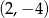 D)
D) 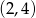
Wierzchołek paraboli 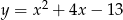 leży na prostej o równaniu
leży na prostej o równaniu
A) 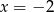 B)
B) 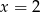 C)
C) 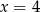 D)
D) 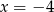
Wierzchołek paraboli 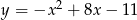 leży na prostej o równaniu
leży na prostej o równaniu
A) 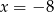 B)
B) 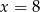 C)
C) 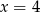 D)
D) 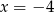
Wierzchołek paraboli 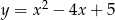 leży na prostej o równaniu
leży na prostej o równaniu
A) 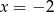 B)
B) 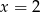 C)
C) 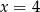 D)
D) 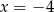
Punkt 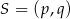 jest wierzchołkiem paraboli będącej wykresem funkcji
jest wierzchołkiem paraboli będącej wykresem funkcji 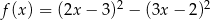 . Zatem
. Zatem
A) 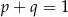 B)
B) 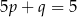 C)
C) 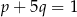 D)
D) 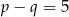
Funkcja kwadratowa 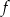 jest określona wzorem
jest określona wzorem 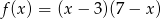 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 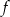 należy do prostej o równaniu
należy do prostej o równaniu
A) 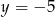 B)
B) 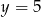 C)
C) 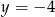 D)
D) 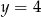
Funkcja kwadratowa 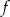 jest określona wzorem
jest określona wzorem 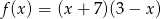 . Wierzchołek paraboli będącej wykresem funkcji
. Wierzchołek paraboli będącej wykresem funkcji 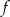 należy do prostej o równaniu
należy do prostej o równaniu
A) 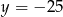 B)
B) 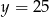 C)
C) 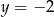 D)
D) 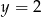
Odległość wierzchołka paraboli 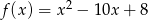 od osi
od osi 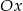 jest równa
jest równa
A) 5 B) 17 C) 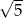 D)
D) 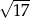
Odległość wierzchołka paraboli 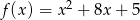 od osi
od osi 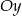 jest równa
jest równa
A) -11 B) 11 C) 4 D) 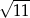
Odległość wierzchołka paraboli 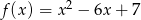 od osi
od osi 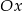 jest równa
jest równa
A) 2 B) -2 C) 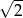 D) 3
D) 3
Wierzchołek 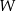 paraboli, będącej wykresem funkcji
paraboli, będącej wykresem funkcji 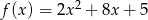 przesunięto o wektor
przesunięto o wektor 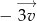 , gdzie
, gdzie ![→ v = [− 4;5]](https://img.zadania.info/zad/6882016/HzadT3x.gif) , otrzymując punkt
, otrzymując punkt 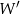 . Współrzędne punktu
. Współrzędne punktu 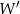 są równe
są równe
A) 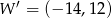 B)
B) 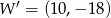 C)
C) 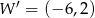 D)
D) 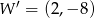
Wierzchołek paraboli opisanej wzorem 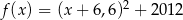 należy do
należy do
A) I ćwiartki układu współrzędnych B) II ćwiartki układu współrzędnych
C) III ćwiartki układu współrzędnych D) IV ćwiartki układu współrzędnych
Dana jest parabola o równaniu 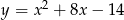 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 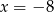 B)
B) 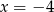 C)
C) 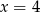 D)
D) 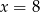
Dana jest parabola o równaniu 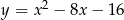 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 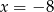 B)
B) 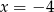 C)
C) 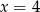 D)
D) 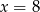
Funkcja kwadratowa 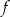 jest określona wzorem
jest określona wzorem 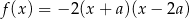 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 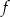 , ma współrzędną
, ma współrzędną 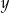 równą 2. Zatem liczba
równą 2. Zatem liczba  może być równa
może być równa
A) 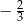 B)
B)  C) 4 D)
C) 4 D) 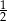
Wierzchołek paraboli będącej wykresem funkcji 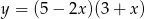 ma współrzędne
ma współrzędne
A) 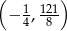 B)
B) 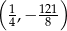 C)
C) 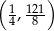 D)
D) 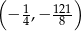
Wierzchołek paraboli będącej wykresem funkcji 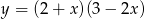 ma współrzędne
ma współrzędne
A) 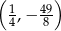 B)
B) 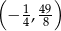 C)
C) 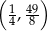 D)
D)