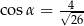Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 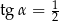 . Zatem
. Zatem
A) 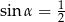 i
i 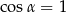 B)
B) 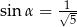 i
i 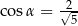
C) 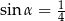 i
i 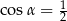 D)
D) 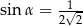 i
i 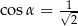
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Dany tangens
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 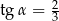 . Zatem
. Zatem
A) 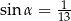 i
i 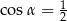 B)
B) 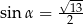 i
i 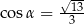
C) 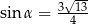 i
i 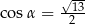 D)
D) 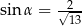 i
i 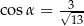
Kąt  jest ostry i
jest ostry i 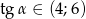 . Wtedy liczba
. Wtedy liczba 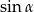 należy do przedziału
należy do przedziału
A) 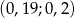 B)
B) 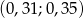 C)
C) 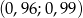 D)
D) 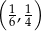
Kąt  jest ostry i
jest ostry i 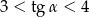 . Wtedy liczba
. Wtedy liczba 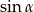 należy do przedziału
należy do przedziału
A) 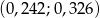 B)
B) 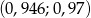 C)
C) 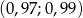 D)
D) 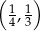
Kąt  jest kątem ostrym i
jest kątem ostrym i 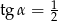 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 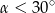 B)
B) 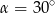 C)
C) 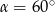 D)
D) 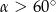
Kąt  jest ostry i
jest ostry i 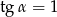 . Wówczas
. Wówczas
A) 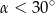 B)
B) 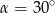 C)
C) 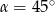 D)
D) 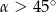
Kąt  jest ostry oraz
jest ostry oraz 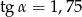 . Zatem
. Zatem
A) 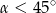 B)
B) 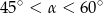 C)
C) 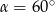 D)
D) 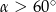
Tangens kąta ostrego  jest równy 0,6. Wówczas
jest równy 0,6. Wówczas
A) 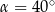 B)
B) 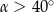 C)
C) 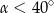 D)
D) 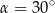
Kąt  jest kątem ostrym i
jest kątem ostrym i 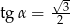 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 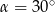 B)
B) 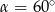 C)
C) 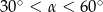 D)
D) 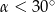
Kąt  jest kątem ostrym i
jest kątem ostrym i 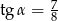 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 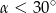 B)
B) 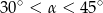 C)
C) 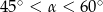 D)
D) 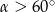
Kąt  jest kątem ostrym i
jest kątem ostrym i 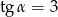 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 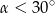 B)
B) 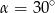 C)
C) 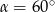 D)
D) 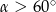
Kąt  jest kątem ostrym i
jest kątem ostrym i 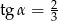 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 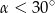 B)
B) 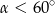 C)
C) 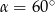 D)
D) 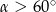
Kąt  jest ostry oraz
jest ostry oraz 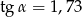 . Zatem
. Zatem
A) 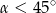 B)
B) 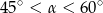 C)
C) 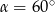 D)
D) 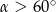
Jeśli 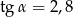 , to wartość wyrażenia
, to wartość wyrażenia 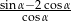 jest równa
jest równa
A) 0,8 B) 1,8 C) 2,6 D) 3,2
Jeśli 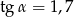 , to wartość wyrażenia
, to wartość wyrażenia 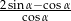 jest równa
jest równa
A) 0,8 B) 1,8 C) 2,6 D) 2,4
Kąt  jest ostry i
jest ostry i 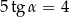 . Wartość wyrażenia
. Wartość wyrażenia 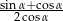 jest równa
jest równa
A) 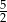 B)
B) 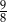 C)
C) 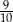 D)
D) 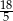
Jeżeli 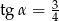 to to stosunek
to to stosunek 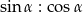 jest równy:
jest równy:
A) 4:3 B) 3:4 C) 1:1 D) 2:3
Jeżeli 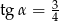 to to stosunek
to to stosunek 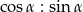 jest równy:
jest równy:
A) 4:3 B) 3:4 C) 1:1 D) 2:3
Jeśli 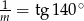 , to
, to
A) 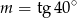 B)
B) 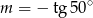 C)
C) 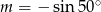 D)
D) 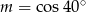
Kąt o mierze  jest ostry i
jest ostry i 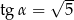 . Wtedy
. Wtedy
A) 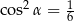 B)
B) 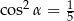 C)
C) 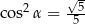 D)
D) 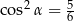
Kąt o mierze  jest ostry i
jest ostry i 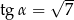 . Wtedy
. Wtedy
A) 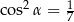 B)
B) 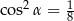 C)
C) 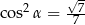 D)
D) 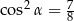
Jeżeli kąt  jest ostry i
jest ostry i 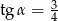 , to
, to 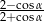 równa się
równa się
A) 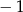 B)
B) 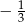 C)
C)  D)
D) 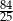
Jeżeli kąt  jest ostry i
jest ostry i 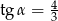 , to
, to 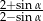 równa się
równa się
A) 1 B)  C) 3 D)
C) 3 D) 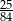
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 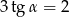 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 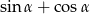 jest równa
jest równa
A) 1 B) 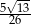 C)
C) 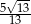 D)
D) 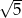
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 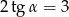 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 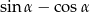 jest równa
jest równa
A) 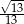 B)
B) 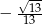 C) 0 D)
C) 0 D) 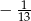
Kąt  jest rozwarty i
jest rozwarty i 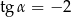 . Wobec tego
. Wobec tego
A) 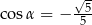 B)
B) 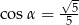 C)
C) 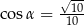 D)
D) 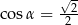
Kąt  jest rozwarty i
jest rozwarty i 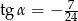 . Wobec tego
. Wobec tego
A) 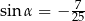 B)
B) 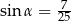 C)
C) 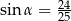 D)
D) 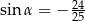
Kąt  jest rozwarty i
jest rozwarty i 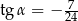 . Wobec tego
. Wobec tego
A) 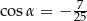 B)
B) 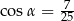 C)
C) 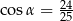 D)
D) 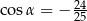
Kąt  jest rozwarty i
jest rozwarty i 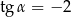 . Wobec tego
. Wobec tego
A) 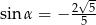 B)
B) 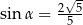 C)
C) 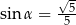 D)
D) 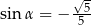
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 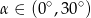 B)
B) 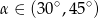 C)
C) 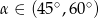 D)
D) 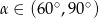
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 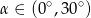 B)
B) 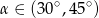 C)
C) 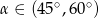 D)
D) 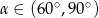
Wiadomo, że tangens kąta ostrego  jest równy
jest równy 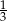 . Wobec tego:
. Wobec tego:
A) 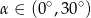 B)
B) 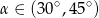 C)
C) 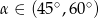 D)
D) 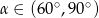
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 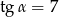 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 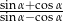 jest równa
jest równa
A) 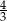 B)
B)  C)
C)  D)
D) 
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 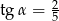 , to wartość wyrażenia
, to wartość wyrażenia 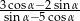 jest równa
jest równa
A) 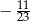 B)
B) 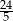 C)
C) 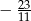 D)
D) 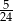
Jeżeli 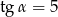 , to wartość wyrażenia
, to wartość wyrażenia 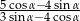 jest równa
jest równa
A) 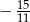 B)
B) 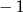 C)
C) 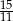 D)
D) 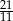
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 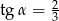 , to wartość wyrażenia
, to wartość wyrażenia 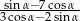 jest równa
jest równa
A) 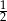 B)
B) 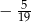 C)
C) 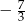 D)
D) 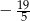
Jeżeli kąt  jest ostry i
jest ostry i 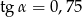 , to wartość wyrażenia
, to wartość wyrażenia 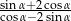 jest równa
jest równa
A) 11 B) 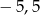 C)
C) 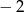 D)
D) 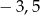
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 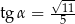 . Wówczas
. Wówczas
A) 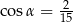 B)
B) 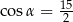 C)
C) 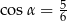 D)
D) 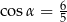
Kąt  jest ostry i
jest ostry i 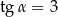 . Wobec tego
. Wobec tego
A) 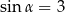 i
i 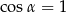 B)
B) 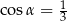 C)
C) 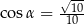 D)
D) 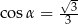
Kąt  jest ostry i
jest ostry i 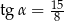 . Wówczas
. Wówczas 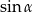 jest równy
jest równy
A) 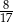 B)
B) 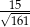 C)
C) 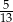 D)
D) 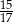
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 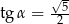 . Wówczas
. Wówczas
A) 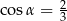 B)
B) 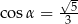 C)
C) 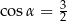 D)
D) 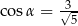
Kąt  jest ostry i
jest ostry i 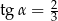 . Wtedy
. Wtedy
A) 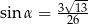 B)
B) 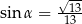 C)
C) 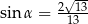 D)
D) 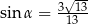
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 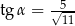 . Wówczas
. Wówczas
A) 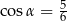 B)
B) 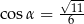 C)
C) 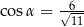 D)
D) 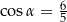
Kąt  jest ostry i
jest ostry i 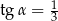 . Wtedy
. Wtedy
A) 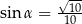 B)
B) 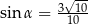 C)
C) 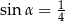 D)
D) 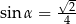
Kąt  jest ostry i
jest ostry i 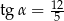 . Wówczas
. Wówczas 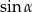 jest równy
jest równy
A) 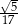 B)
B) 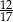 C)
C) 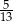 D)
D) 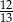
Kąt  jest ostry i
jest ostry i 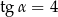 . Wobec tego
. Wobec tego
A) 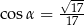 B)
B) 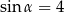 i
i 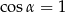 C)
C) 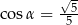 D)
D) 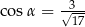
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 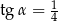 . Zatem
. Zatem
A) 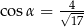 B)
B) 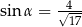 C)
C) 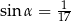 D)
D) 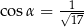
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 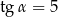 . Zatem
. Zatem
A) 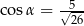 B)
B) 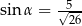 C)
C) 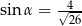 D)
D)