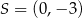Punkt 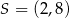 jest środkiem odcinka
jest środkiem odcinka 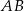 , gdzie
, gdzie 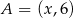 i
i 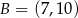 dla
dla  równego
równego
A) 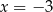 B)
B) 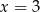 C)
C) 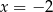 D)
D) 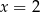
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Odcinek
Punkt 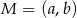 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 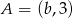 i
i 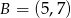 . Wówczas
. Wówczas
A) 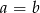 B)
B) 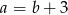 C)
C) 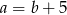 D)
D) 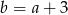
Punkt 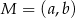 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 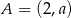 i
i 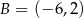 . Wówczas
. Wówczas
A) 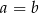 B)
B) 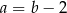 C)
C) 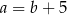 D)
D) 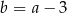
Punkt 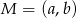 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 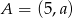 i
i 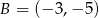 . Wówczas
. Wówczas
A) 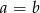 B)
B) 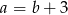 C)
C) 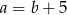 D)
D) 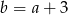
W układzie współrzędnych dane są punkty 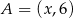 ,
, 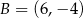 oraz
oraz 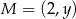 . Jeżeli punkt
. Jeżeli punkt 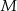 jest środkiem odcinka
jest środkiem odcinka 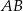 , to
, to
A) 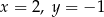 B)
B) 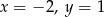 C)
C) 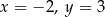 D)
D) 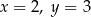
W układzie współrzędnych dane są punkty 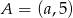 oraz
oraz 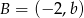 . Środkiem odcinka
. Środkiem odcinka 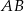 jest punkt
jest punkt 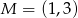 . Wynika stąd, że
. Wynika stąd, że
A) 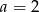 i
i 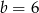 B)
B) 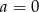 i
i 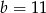 C)
C) 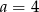 i
i 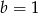 D)
D) 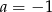 i
i 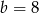
Środkiem odcinka o końcach 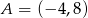 i
i 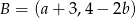 jest początek prostokątnego układu współrzędnych. Wówczas
jest początek prostokątnego układu współrzędnych. Wówczas
A) 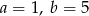 B)
B) 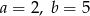 C)
C) 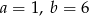 D)
D) 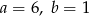
Jeżeli 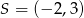 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 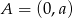 i
i 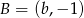 , to
, to
A) 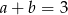 B)
B) 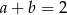 C)
C) 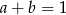 D)
D) 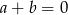
W układzie współrzędnych dane są punkty 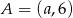 oraz
oraz 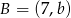 . Środkiem odcinka
. Środkiem odcinka 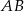 jest punkt
jest punkt 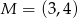 . Wynika stąd, że
. Wynika stąd, że
A) 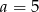 i
i 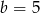 B)
B) 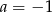 i
i 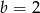 C)
C) 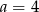 i
i 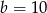 D)
D) 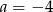 i
i 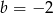
Punkty 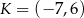 i
i 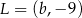 są końcami odcinka
są końcami odcinka 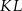 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 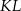 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 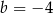 B)
B) 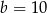 C)
C) 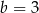 D)
D) 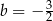
Obrazem odcinka 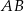 o końcach w punktach
o końcach w punktach 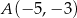 ,
, 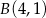 w symetrii względem osi
w symetrii względem osi 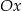 , jest odcinek
, jest odcinek 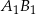 o końcach w punktach
o końcach w punktach
A) 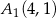 ,
, 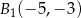 B)
B) 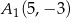 ,
, 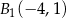
C) 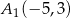 ,
, 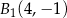 D)
D) 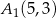 ,
, 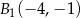
Dane są punkty 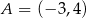 i
i 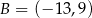 . Punkt
. Punkt 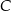 należący do odcinka
należący do odcinka 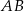 i taki, że
i taki, że 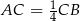 ma współrzędne
ma współrzędne
A) 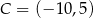 B)
B) 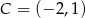 C)
C) 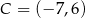 D)
D) 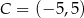
Punkt 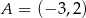 jest końcem odcinka
jest końcem odcinka 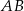 , a punkt
, a punkt 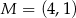 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 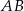 jest równa
jest równa
A) 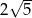 B)
B) 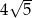 C)
C) 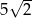 D)
D) 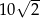
Punkt 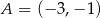 jest końcem odcinka
jest końcem odcinka 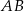 , a punkt
, a punkt 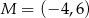 jest środkiem tego odcinka. Długość odcinka
jest środkiem tego odcinka. Długość odcinka 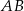 jest równa
jest równa
A) 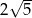 B)
B) 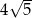 C)
C) 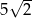 D)
D) 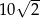
W układzie współrzędnych na płaszczyźnie dany jest odcinek 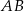 o końcach w punktach
o końcach w punktach 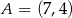 ,
, 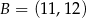 . Punkt
. Punkt 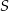 leży wewnątrz odcinka
leży wewnątrz odcinka 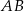 oraz
oraz 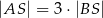 . Wówczas
. Wówczas
A) 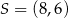 B)
B) 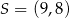 C)
C) 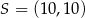 D)
D) 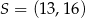
W układzie współrzędnych na płaszczyźnie dany jest odcinek 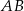 o końcach w punktach
o końcach w punktach 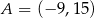 ,
, 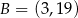 . Punkt
. Punkt 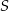 leży wewnątrz odcinka
leży wewnątrz odcinka 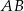 oraz
oraz 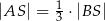 . Wówczas
. Wówczas
A) 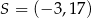 B)
B) 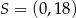 C)
C) 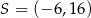 D)
D) 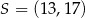
Długość odcinka 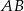 o końcach
o końcach 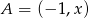 i
i 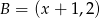 jest równa 6. Wtedy
jest równa 6. Wtedy
A) 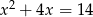 B)
B) 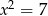 C)
C) 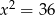 D)
D)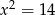
Odcinek o końcach 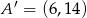 i
i 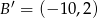 jest obrazem odcinka
jest obrazem odcinka 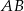 w jednokładności o skali
w jednokładności o skali 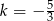 . Długość odcinka
. Długość odcinka 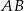 jest równa
jest równa
A) 12 B) 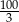 C) 16 D)
C) 16 D) 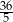
Odcinek o końcach 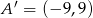 i
i 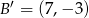 jest obrazem odcinka
jest obrazem odcinka 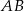 w jednokładności o skali
w jednokładności o skali 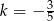 . Długość odcinka
. Długość odcinka 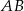 jest równa
jest równa
A) 12 B) 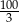 C) 16 D)
C) 16 D) 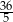
Przez punkt 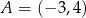 poprowadzono prostą
poprowadzono prostą 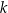 , która przecina proste
, która przecina proste 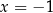 i
i 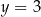 w takich punktach
w takich punktach 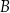 i
i 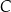 , że
, że 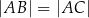 . Długość odcinka
. Długość odcinka 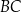 jest równa
jest równa
A) 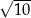 B)
B) 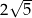 C)
C) 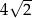 D)
D) 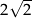
W kartezjańskim układzie współrzędnych 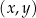 dane są punkty
dane są punkty 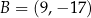 oraz
oraz 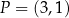 . Punkt
. Punkt 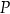 dzieli odcinek
dzieli odcinek 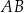 tak, że
tak, że 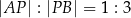 . Punkt
. Punkt 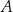 ma współrzędne
ma współrzędne
A) 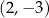 B)
B) 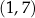 C)
C) 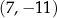 D)
D) 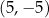
Punkty 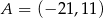 i
i 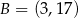 są końcami odcinka
są końcami odcinka 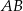 . Obrazem tego odcinka w symetrii względem osi
. Obrazem tego odcinka w symetrii względem osi 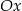 układu współrzędnych jest odcinek
układu współrzędnych jest odcinek 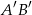 . Środkiem odcinka
. Środkiem odcinka 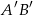 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 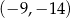 B)
B) 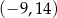 C)
C) 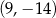 D)
D) 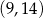
Punkty 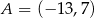 i
i 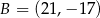 są końcami odcinka
są końcami odcinka 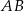 . Obrazem tego odcinka w symetrii względem osi
. Obrazem tego odcinka w symetrii względem osi 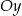 układu współrzędnych jest odcinek
układu współrzędnych jest odcinek 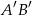 . Środkiem odcinka
. Środkiem odcinka 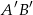 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 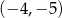 B)
B) 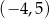 C)
C) 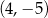 D)
D) 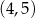
Punkt 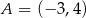 jest końcem odcinka
jest końcem odcinka 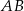 , a punkt
, a punkt 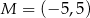 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 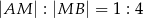 . Długość odcinka
. Długość odcinka 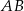 jest równa
jest równa
A) 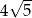 B)
B) 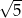 C)
C) 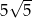 D)
D) 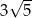
Punkt 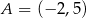 jest końcem odcinka
jest końcem odcinka 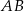 , a punkt
, a punkt 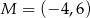 jest takim punktem tego odcinka, że
jest takim punktem tego odcinka, że 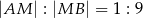 . Długość odcinka
. Długość odcinka 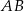 jest równa
jest równa
A) 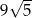 B)
B) 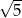 C)
C) 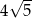 D)
D) 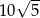
Dane są punkty 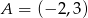 oraz
oraz 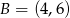 . Długość odcinka
. Długość odcinka 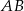 jest równa
jest równa
A) 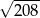 B)
B) 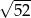 C)
C) 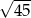 D)
D) 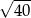
Dane są punkty 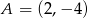 oraz
oraz 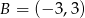 . Odcinek
. Odcinek 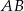 ma długość
ma długość
A) 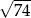 B)
B) 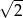 C)
C) 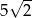 D)
D) 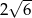
Dane są punkty 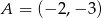 oraz
oraz 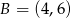 . Długość odcinka
. Długość odcinka 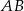 jest równa
jest równa
A) 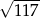 B)
B) 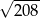 C)
C) 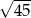 D)
D) 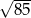
Dane są punkty: 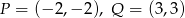 . Odległość punktu
. Odległość punktu 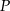 od punktu
od punktu 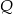 jest równa
jest równa
A) 1 B) 5 C) 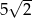 D)
D) 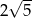
Dane są punkty 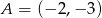 oraz
oraz 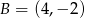 . Długość odcinka
. Długość odcinka 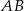 jest równa
jest równa
A) 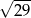 B)
B) 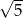 C)
C) 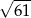 D)
D) 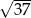
Dane są punkty 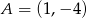 oraz
oraz 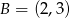 . Odcinek
. Odcinek 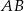 ma długość
ma długość
A) 1 B) 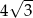 C)
C) 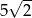 D) 7
D) 7
Dane są punkty 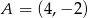 oraz
oraz 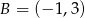 . Długość odcinka
. Długość odcinka 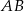 jest równa
jest równa
A) 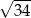 B)
B) 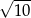 C)
C) 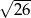 D)
D) 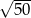
Długość odcinka 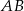 o końcach w punktach
o końcach w punktach 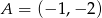 i
i 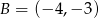 jest równa
jest równa
A) 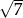 B)
B) 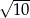 C)
C) 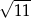 D)
D) 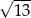
Długość odcinka 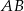 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 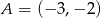 i
i 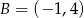 , jest równa:
, jest równa:
A) 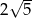 B)
B) 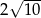 C)
C) 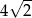 D)
D) 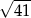
Punkt 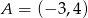 jest początkiem odcinka
jest początkiem odcinka 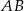 , gdzie
, gdzie 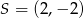 jest jego środkiem. Punkt
jest jego środkiem. Punkt 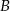 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 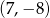 B)
B) 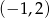 C)
C) 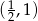 D)
D) 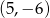
Punkt 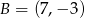 jest końcem odcinka
jest końcem odcinka 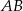 , gdzie
, gdzie 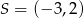 jest jego środkiem. Punkt
jest jego środkiem. Punkt 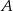 , który jest początkiem tego odcinka ma współrzędne
, który jest początkiem tego odcinka ma współrzędne
A) 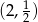 B)
B) 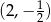 C)
C) 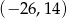 D)
D) 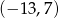
Punkt 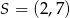 jest środkiem odcinka
jest środkiem odcinka 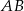 , w którym
, w którym 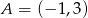 . Punkt
. Punkt 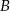 ma współrzędne:
ma współrzędne:
A) 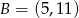 B)
B) 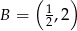 C)
C) 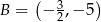 D)
D) 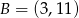
Punkt 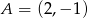 jest początkiem odcinka
jest początkiem odcinka 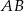 , gdzie
, gdzie 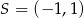 jest jego środkiem. Punkt
jest jego środkiem. Punkt 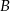 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 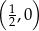 B)
B) 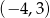 C)
C) 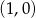 D)
D) 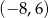
W układzie współrzędnych punkt 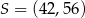 jest środkiem odcinka
jest środkiem odcinka 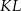 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 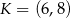 . Zatem
. Zatem
A) 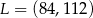 B)
B) 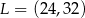 C)
C) 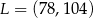 D)
D) 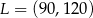
Punkt 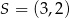 jest środkiem odcinka
jest środkiem odcinka 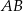 , w którym
, w którym 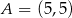 . Punkt
. Punkt 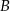 ma współrzędne
ma współrzędne
A) 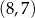 B)
B) 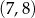 C)
C) 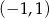 D)
D) 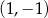
Punkt 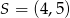 jest środkiem odcinka
jest środkiem odcinka 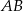 , w którym
, w którym 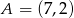 . Punkt
. Punkt 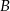 ma współrzędne:
ma współrzędne:
A) 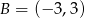 B)
B) 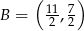 C)
C) 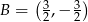 D)
D) 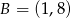
Punkt 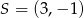 jest środkiem odcinka
jest środkiem odcinka 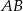 i
i 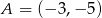 . Punkt
. Punkt 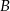 ma współrzędne
ma współrzędne
A) 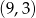 B)
B) 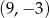 C)
C) 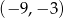 D)
D) 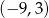
Punkt 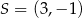 jest środkiem odcinka
jest środkiem odcinka 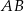 , w którym
, w którym 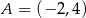 . Punkt
. Punkt 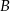 ma współrzędne
ma współrzędne
A) 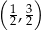 B)
B) 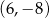 C)
C) 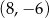 D)
D) 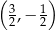
W układzie współrzędnych zaznaczono dwa punkty: 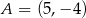 i
i 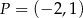 . Punkt
. Punkt 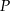 jest środkiem odcinka
jest środkiem odcinka 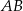 . Jakie współrzędne ma punkt B?
. Jakie współrzędne ma punkt B?
A) 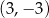 B)
B) 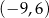 C)
C) 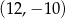 D)
D) 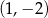
W układzie współrzędnych punkt 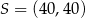 jest środkiem odcinka
jest środkiem odcinka 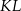 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 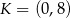 . Zatem
. Zatem
A) 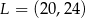 B)
B) 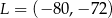 C)
C) 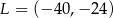 D)
D) 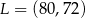
Punkt 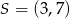 jest środkiem odcinka
jest środkiem odcinka 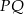 , gdzie
, gdzie 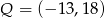 . Zatem punkt
. Zatem punkt 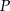 ma współrzędne
ma współrzędne
A) 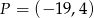 B)
B) 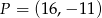 C)
C) 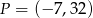 D)
D) 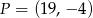
Punkt 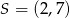 jest środkiem odcinka
jest środkiem odcinka 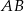 , w którym
, w którym 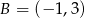 . Punkt
. Punkt 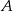 ma współrzędne:
ma współrzędne:
A) 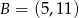 B)
B) 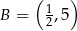 C)
C) 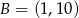 D)
D) 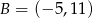
Dane są punkty 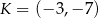 oraz
oraz 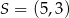 . Punkt
. Punkt 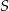 jest środkiem odcinka
jest środkiem odcinka 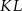 . Wtedy punkt
. Wtedy punkt 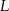 ma współrzędne
ma współrzędne
A) 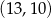 B)
B) 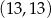 C)
C) 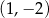 D)
D) 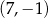
W układzie współrzędnych zaznaczono dwa punkty: 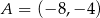 i
i 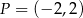 . Punkt
. Punkt 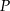 jest środkiem odcinka
jest środkiem odcinka 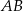 . Jakie współrzędne ma punkt
. Jakie współrzędne ma punkt 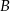 ?
?
A) 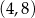 B)
B) 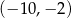 C)
C) 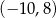 D)
D) 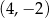
Punkt 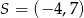 jest środkiem odcinka
jest środkiem odcinka 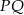 , gdzie
, gdzie 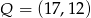 . Zatem punkt
. Zatem punkt 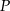 ma współrzędne
ma współrzędne
A) 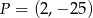 B)
B) 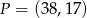 C)
C) 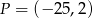 D)
D) 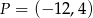
Punkt 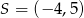 jest środkiem odcinka
jest środkiem odcinka 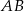 i
i 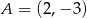 . Punkt
. Punkt 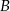 ma współrzędne
ma współrzędne
A) 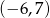 B)
B) 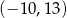 C)
C) 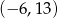 D)
D) 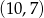
Jeżeli punkty 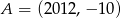 i
i 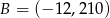 są końcami odcinka
są końcami odcinka 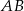 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych
A) 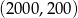 B)
B) 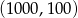 C)
C) 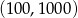 D)
D) 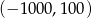
Jeżeli punkty 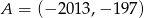 i
i 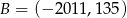 są końcami odcinka
są końcami odcinka 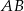 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych
A) 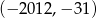 B)
B) 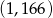 C)
C) 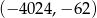 D)
D) 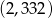
Dany jest odcinek 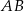 , gdzie
, gdzie 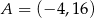 i
i 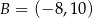 oraz prosta
oraz prosta 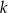 o równaniu
o równaniu 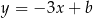 . Jeżeli prosta
. Jeżeli prosta 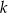 przecina odcinek
przecina odcinek 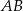 w takim punkcie
w takim punkcie 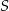 , że
, że 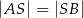 , to liczba
, to liczba 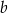 jest równa
jest równa
A) 31 B) 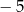 C) 4 D)
C) 4 D) 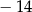
Dany jest odcinek 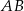 , gdzie
, gdzie 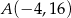 ,
, 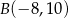 . Punkt
. Punkt  jest środkiem odcinka
jest środkiem odcinka 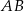 . Obrazem punktu
. Obrazem punktu 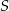 w symetrii względem osi
w symetrii względem osi 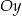 jest punkt
jest punkt
A) 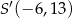 B)
B) 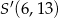 C)
C) 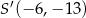 D)
D) 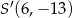
Dany jest odcinek 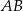 , gdzie
, gdzie 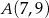 ,
, 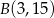 . Punkt
. Punkt 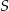 jest środkiem odcinka
jest środkiem odcinka 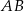 . Obrazem punktu
. Obrazem punktu 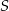 w symetrii względem osi
w symetrii względem osi 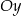 jest punkt
jest punkt
A) 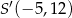 B)
B) 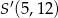 C)
C) 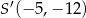 D)
D) 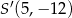
Punkt 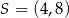 jest środkiem odcinka
jest środkiem odcinka 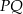 , którego koniec
, którego koniec 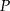 leży na osi
leży na osi 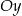 , a koniec
, a koniec 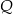 – na osi
– na osi 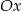 . Wynika stąd, że
. Wynika stąd, że
A) 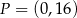 i
i 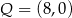 B)
B) 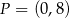 i
i 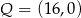
C) 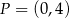 i
i 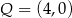 D)
D) 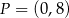 i
i 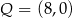
Punkt 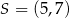 jest środkiem odcinka
jest środkiem odcinka 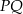 , którego koniec
, którego koniec 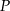 leży na osi
leży na osi 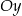 , a koniec
, a koniec 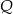 – na osi
– na osi 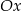 . Wynika stąd, że
. Wynika stąd, że
A) 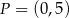 i
i 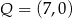 B)
B) 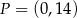 i
i 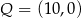
C) 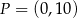 i
i 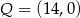 D)
D) 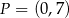 i
i 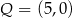
Punkt 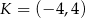 jest końcem odcinka
jest końcem odcinka 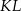 , punkt
, punkt 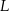 leży na osi
leży na osi 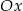 , a środek
, a środek 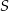 tego odcinka leży na osi
tego odcinka leży na osi 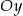 . Wynika stąd, że
. Wynika stąd, że
A) 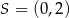 B)
B) 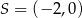 C)
C) 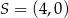 D)
D) 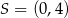
Punkt 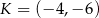 jest końcem odcinka
jest końcem odcinka 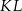 , punkt
, punkt 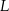 leży na osi
leży na osi 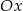 , a środek
, a środek 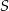 tego odcinka leży na osi
tego odcinka leży na osi 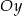 . Wynika stąd, że
. Wynika stąd, że
A) 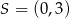 B)
B) 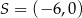 C)
C) 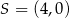 D)
D)