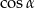Dla każdego kąta  wyrażenie
wyrażenie 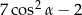 jest równe
jest równe
A) 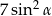 B)
B) 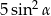
C)  D)
D) 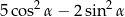
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Wartość wyrażenia/Z literką
Wyrażenie 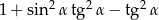 może być przekształcone do postaci
może być przekształcone do postaci
A) 1 B) 0 C) 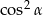 D)
D) 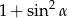
Dla każdego kąta ostrego  wyrażenie
wyrażenie 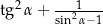 jest równe
jest równe
A) 1 B)  C)
C) 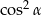 D)
D) 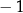
Wyrażenie 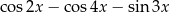 jest równe
jest równe
A) 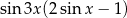 B)
B) 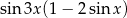
C) 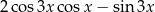 D)
D) 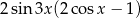
Wyrażenie 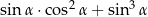 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 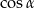 B) 1 C)
B) 1 C)  D)
D) 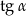
Wyrażenie 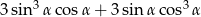 może być przekształcone do postaci
może być przekształcone do postaci
A) 3 B) 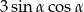 C)
C) 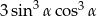 D)
D) 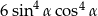
Wyrażenie 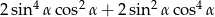 może być przekształcone do postaci
może być przekształcone do postaci
A) 2 B) 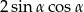 C)
C) 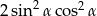 D)
D) 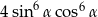
Dla każdego kąta ostrego  wyrażenie
wyrażenie 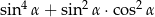 jest równe
jest równe
A) 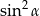 B)
B) 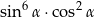
C) 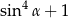 D)
D) 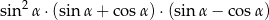
Dla każdego kąta ostrego  wyrażenie
wyrażenie 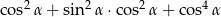 jest równe
jest równe
A) 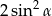 B)
B) 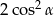 C) 1 D) 2
C) 1 D) 2
Dla każdego kąta ostrego  wyrażenie
wyrażenie 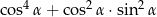 jest równe
jest równe
A) 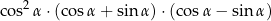 B)
B) 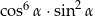
C) 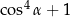 D)
D) 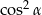
Dla każdego kąta ostrego  wyrażenie
wyrażenie 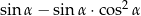 jest równe
jest równe
A) 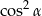 B)
B) 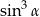 C)
C) 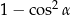 D)
D) 
Dla każdego kąta ostrego  wyrażenie
wyrażenie 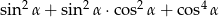 jest równe
jest równe
A) 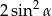 B)
B) 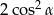 C) 1 D) 2
C) 1 D) 2
Dla każdego kąta ostrego  wyrażenie
wyrażenie 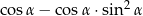 jest równe
jest równe
A) 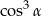 B)
B) 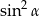 C)
C)  D)
D) 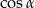
Wyrażenie 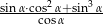 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 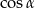 B) 1 C)
B) 1 C) 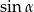 D)
D) 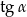
Wyrażenie 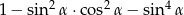 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 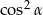 B) 1 C)
B) 1 C) 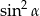 D)
D) 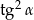
Wyrażenie 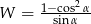 można zapisać w postaci
można zapisać w postaci
A) 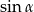 B)
B) 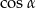 C)
C) 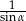 D) 1
D) 1
Wyrażenie 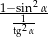 , gdzie
, gdzie  jest kątem ostrym, można zapisać w postaci
jest kątem ostrym, można zapisać w postaci
A) 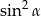 B)
B) 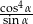 C)
C) 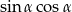 D)
D) 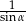
Wyrażenie 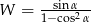 można zapisać w postaci
można zapisać w postaci
A) 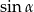 B)
B) 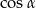 C)
C) 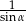 D) 1
D) 1
Wyrażenie 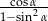 można zapisać w postaci:
można zapisać w postaci:
A) 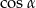 B)
B) 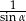 C)
C) 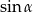 D)
D) 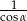
Wyrażenie 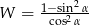 można zapisać w postaci
można zapisać w postaci
A) 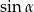 B)
B) 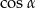 C)
C) 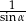 D) 1
D) 1
Wyrażenie 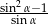 dla kąta ostrego
dla kąta ostrego  jest równe
jest równe
A) 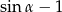 B)
B) 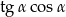 C)
C) 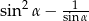 D)
D) 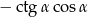
Zbiorem wartości funkcji 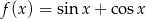 , gdzie
, gdzie 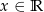 , jest przedział
, jest przedział
A) 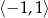 B)
B) 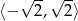 C)
C) 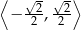 D)
D) 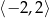
Wyrażenie 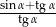 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 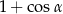 B)
B) 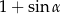 C)
C) 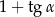 D)
D) 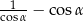
Wyrażenie 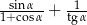 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 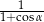 B)
B) 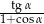 C)
C) 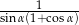 D)
D) 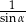
Wyrażenie 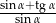 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 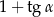 B)
B) 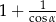 C)
C) 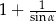 D)
D) 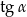
Wyrażenie 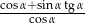 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 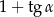 B)
B) 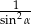 C)
C) 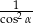 D)
D) 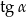
Dla ostrego kąta  wyrażenie
wyrażenie 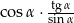 jest równe
jest równe
A) 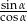 B)
B) 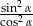 C)
C) 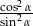 D)
D) 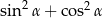
Dla dowolnego kąta  wartość wyrażenia
wartość wyrażenia 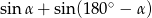 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 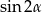 B)
B) 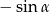 C)
C) 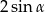 D) 0
D) 0
Dla dowolnego kąta  wartość wyrażenia
wartość wyrażenia 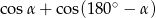 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 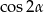 B)
B) 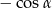 C)
C) 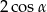 D) 0
D) 0
Kąt  jest ostry oraz wiadomo, że
jest ostry oraz wiadomo, że 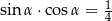 . Wartość wyrażenia
. Wartość wyrażenia 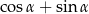 jest równa
jest równa
A) 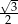 B)
B) 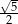 C)
C)  D)
D) 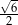
Wyrażenie 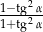 jest równe
jest równe
A) 1 B) 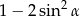 C) 0 D)
C) 0 D) 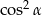
Kąt 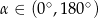 oraz wiadomo, że
oraz wiadomo, że 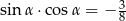 . Wartość wyrażenia
. Wartość wyrażenia 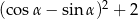 jest równa
jest równa
A) 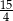 B)
B)  C)
C) 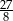 D)
D) 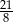
Kąt 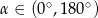 spełnia warunek:
spełnia warunek: 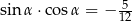 . Wartość wyrażenia
. Wartość wyrażenia 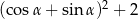 jest równa
jest równa
A) 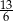 B)
B) 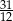 C)
C) 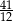 D)
D) 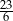
Jeżeli 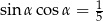 , wartość liczbowa wyrażenia
, wartość liczbowa wyrażenia 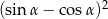 jest równa
jest równa
A)  B)
B)  C)
C)  D) 1
D) 1
Dla każdego  suma
suma 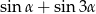 jest równa
jest równa
A) 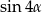 B)
B) 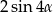 C)
C) 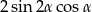 D)
D) 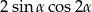
Dla każdego  różnica
różnica 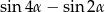 jest równa
jest równa
A) 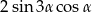 B)
B) 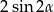 C)
C) 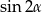 D)
D) 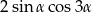
Dla każdego  różnica
różnica 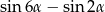 jest równa
jest równa
A) 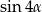 B)
B) 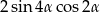 C)
C) 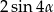 D)
D) 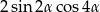
Dla każdego  suma
suma 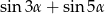 jest równa
jest równa
A) 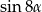 B)
B) 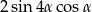 C)
C) 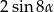 D)
D) 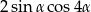
Dla każdego  suma
suma 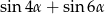 jest równa
jest równa
A) 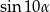 B)
B) 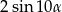 C)
C) 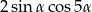 D)
D) 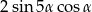
Dla każdego  różnica
różnica 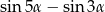 jest równa
jest równa
A) 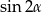 B)
B) 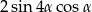 C)
C) 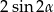 D)
D) 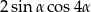
Dla każdego  suma
suma 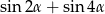 jest równa
jest równa
A) 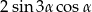 B)
B) 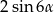 C)
C) 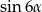 D)
D) 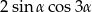
Dla każdego  różnica
różnica 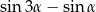 jest równa
jest równa
A) 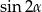 B)
B) 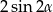 C)
C) 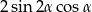 D)
D) 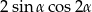
Dla każdego  suma
suma 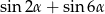 jest równa
jest równa
A) 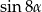 B)
B) 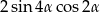 C)
C) 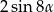 D)
D) 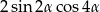
Dla każdego  różnica
różnica 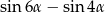 jest równa
jest równa
A) 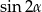 B)
B) 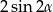 C)
C) 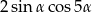 D)
D) 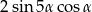
Miara kąta  spełnia warunek:
spełnia warunek: 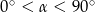 . Wyrażenie
. Wyrażenie 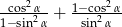 jest równe
jest równe
A) 1 B) 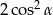 C) 2 D)
C) 2 D) 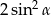
Dla każdego kąta  , spełniającego warunek:
, spełniającego warunek: 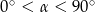 , wyrażenie
, wyrażenie 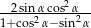 jest równe
jest równe
A) 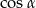 B)
B) 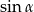 C)
C) 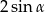 D)
D) 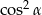
Dla każdego kąta ostrego  iloczyn
iloczyn 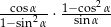 jest równy
jest równy
A) 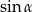 B)
B) 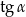 C)
C) 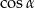 D)
D) 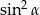
Dla każdego kąta ostrego  iloczyn
iloczyn 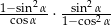 jest równy
jest równy
A) 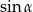 B)
B) 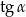 C)
C) 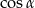 D)
D) 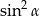
Wyrażenie 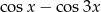 jest równe
jest równe
A) 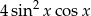 B)
B) 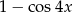 C)
C) 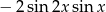 D)
D) 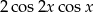
Wyrażenie 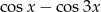 jest równe
jest równe
A) 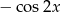 B)
B) 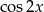 C)
C) 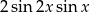 D)
D) 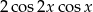
Wyrażenie 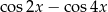 jest równe
jest równe
A) 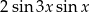 B)
B) 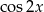 C)
C) 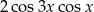 D)
D) 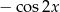
Wyrażenie 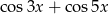 jest równe
jest równe
A) 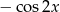 B)
B) 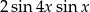 C)
C) 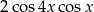 D)
D) 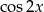
Wyrażenie 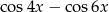 jest równe
jest równe
A) 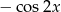 B)
B) 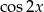 C)
C) 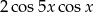 D)
D) 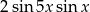
Wyrażenie 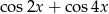 jest równe
jest równe
A) 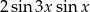 B)
B) 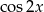 C)
C) 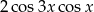 D)
D) 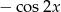
Wyrażenie 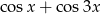 jest równe
jest równe
A) 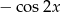 B)
B) 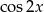 C)
C) 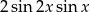 D)
D) 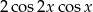
Wyrażenie 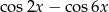 jest równe
jest równe
A) 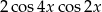 B)
B) 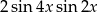 C)
C) 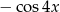 D)
D) 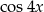
Wyrażenie 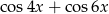 jest równe
jest równe
A) 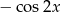 B)
B) 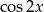 C)
C) 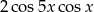 D)
D) 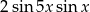
Wyrażenie 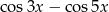 jest równe
jest równe
A) 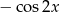 B)
B) 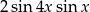 C)
C) 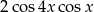 D)
D) 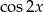
Wyrażenie 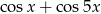 jest równe
jest równe
A) 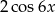 B)
B) 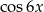 C)
C) 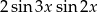 D)
D) 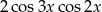
Wyrażenie 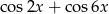 jest równe
jest równe
A) 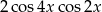 B)
B) 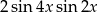 C)
C) 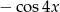 D)
D) 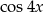
Wyrażenie 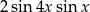 jest równe
jest równe
A) 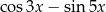 B)
B) 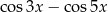 C)
C) 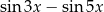 D)
D) 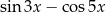
Wyrażenie 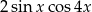 jest równe
jest równe
A) 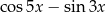 B)
B) 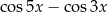 C)
C) 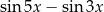 D)
D) 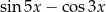
Wyrażenie 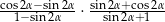 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 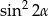 B)
B) 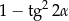 C)
C) 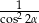 D)
D) 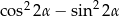
W trójkącie prostokątnym dane są kąty ostre: 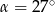 i
i 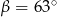 . Wtedy
. Wtedy 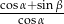 równa się
równa się
A) 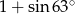 B)
B) 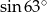 C) 1 D) 2
C) 1 D) 2
W trójkącie prostokątnym dane są kąty ostre: 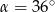 i
i 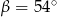 . Wtedy
. Wtedy 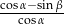 równa się
równa się
A) 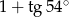 B)
B) 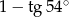 C) 1 D) 0
C) 1 D) 0
Wartość wyrażenia 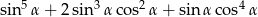 jest równa
jest równa
A) 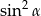 B)
B) 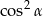 C)
C) 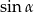 D)
D) 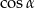
Wyrażenie 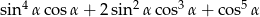 jest równe
jest równe
A) 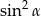 B)
B) 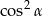 C)
C) 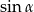 D)
D)