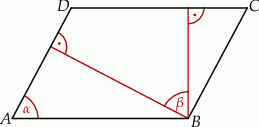
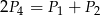Odcinek 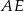 jest dwusieczną kąta
jest dwusieczną kąta 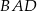 w równoległoboku
w równoległoboku 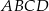 . Miara kąta
. Miara kąta 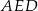 jest równa
jest równa 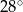 .
.
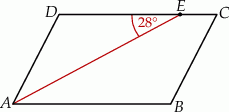
Miara kąta 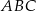 jest równa
jest równa
A) 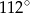 B)
B) 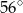 C)
C) 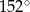 D)
D) 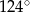
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinek 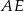 jest dwusieczną kąta
jest dwusieczną kąta 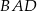 w równoległoboku
w równoległoboku 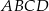 . Miara kąta
. Miara kąta 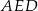 jest równa
jest równa 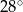 .
.

Miara kąta 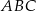 jest równa
jest równa
A) 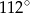 B)
B) 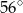 C)
C) 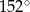 D)
D) 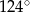
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 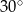 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 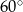 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 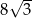 B)
B) 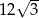 C)
C) 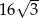 D)
D) 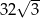
Jeden bok równoległoboku ma długość 120 cm, a drugi ma długość 60 cm. Przekątna tego równoległoboku może mieć długość
A) 50 cm B) 60 cm C) 120 cm D) 200 cm
W równoległoboku 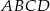 mamy dane
mamy dane 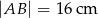 i
i 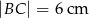 . Jedna z wysokości tego równoległoboku ma długość
. Jedna z wysokości tego równoległoboku ma długość 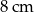 . Zatem kąt ostry równoległoboku jest równy
. Zatem kąt ostry równoległoboku jest równy
A) 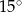 B)
B) 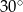 C)
C) 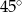 D)
D) 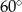
Pole równoległoboku o bokach długości 4 i 12 oraz kącie ostrym 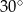 jest równe
jest równe
A) 24 B) 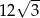 C) 12 D)
C) 12 D) 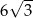
Pole równoległoboku o bokach długości 6 i 10 oraz kącie ostrym 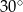 jest równe
jest równe
A) 60 B) 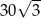 C) 30 D)
C) 30 D) 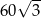
Pole równoległoboku o kącie ostrym równym 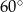 i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
A) 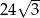 B)
B) 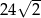 C) 24 D)
C) 24 D) 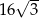
Pole równoległoboku 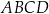 jest równe
jest równe 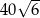 . Bok
. Bok 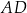 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 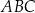 równoległoboku ma miarę
równoległoboku ma miarę 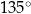 (zobacz rysunek).
(zobacz rysunek).

Długość boku 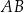 jest równa
jest równa
A) 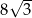 B)
B) 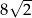 C)
C) 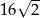 D)
D) 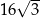
Pole równoległoboku 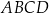 jest równe
jest równe 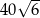 . Bok
. Bok 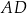 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 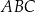 równoległoboku ma miarę
równoległoboku ma miarę 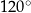 (zobacz rysunek).
(zobacz rysunek).

Długość boku 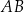 jest równa
jest równa
A) 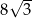 B)
B) 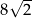 C)
C) 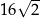 D)
D) 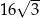
W równoległoboku 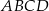 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 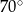 .
.
Wtedy kąt 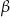 ma miarę
ma miarę
A) 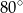 B)
B) 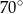 C)
C) 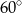 D)
D) 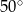
W równoległoboku 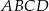 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 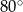 .
.
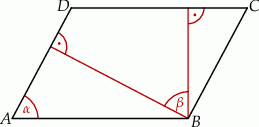
Wtedy kąt 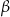 ma miarę
ma miarę
A) 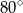 B)
B) 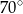 C)
C) 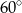 D)
D) 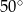
Pole powierzchni równoległoboku jest równe 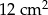 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 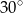 . Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
. Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole powierzchni równoległoboku jest równe 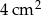 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 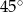 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 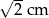 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole powierzchni równoległoboku jest równe 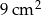 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 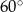 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 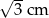 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole równoległoboku 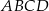 jest równe 120. Na bokach
jest równe 120. Na bokach 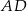 i
i 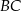 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 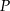 i
i 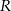 , takie, że
, takie, że 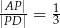 i
i 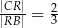 (zobacz rysunek)
(zobacz rysunek)
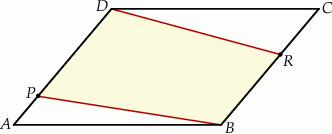
Pole czworokąta 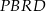 jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
Przekątne dzielą równoległobok na cztery trójkąty
A) przystające B) podobne C) o równych polach D) o równych obwodach
W równoległoboku 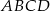 dłuższa podstawa ma długość
dłuższa podstawa ma długość 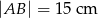 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 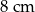 i
i 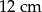 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości
A) 4 i 6 B) 4 i 3 C) 10 i 10 D) 5 i 5
Jeden z boków równoległoboku ma długość równą 12. Przekątne tego równoległoboku mogą mieć długości
A) 10 i 10 B) 18 i 6 C) 12 i 12 D) 30 i 30
Pole równoległoboku o bokach długości 6 i 8 oraz kącie rozwartym 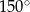 jest równe
jest równe
A) 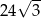 B) 48 C)
B) 48 C) 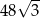 D) 24
D) 24
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 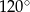 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 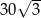 B) 30 C)
B) 30 C) 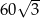 D) 60
D) 60
Pole równoległoboku o bokach długości 4 i 7 oraz kącie rozwartym 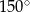 jest równe
jest równe
A) 14 B) 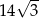 C)
C) 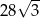 D) 28
D) 28
Pole równoległoboku o bokach długości 6 cm i 10 cm i kącie rozwartym o mierze 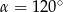 jest równe
jest równe
A) 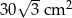 B)
B) 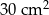 C)
C) 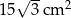 D)
D) 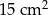
Dany jest równoległobok o bokach długości 3 i 4 oraz o kącie między nimi o mierze 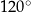 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 12 B) 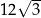 C) 6 D)
C) 6 D) 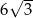
Boki równoległoboku mają długość 8 cm i 10 cm, a jego pole wynosi 40 cm. Kąt ostry równoległoboku ma miarę:
A) 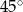 B)
B) 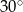 C)
C) 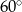 D)
D) 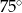
Boki równoległoboku mają długości: 6 cm i 10 cm, a jego pole wynosi 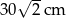 . Kąt ostry równoległoboku ma miarę:
. Kąt ostry równoległoboku ma miarę:
A) 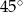 B)
B) 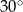 C)
C) 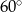 D)
D) 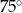
W równoległoboku 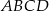 na przekątnej
na przekątnej 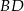 wybrano punkty
wybrano punkty 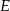 i
i 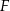 tak, że
tak, że 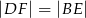 (zobacz rysunek). Dane są ponadto:
(zobacz rysunek). Dane są ponadto: 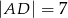 ,
, 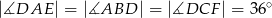 .
.
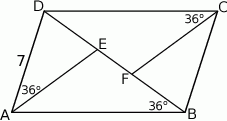
Wówczas długość odcinka 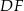 jest równa
jest równa
A) 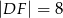 B)
B) 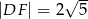 C)
C) 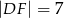 D)
D) 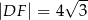
W równoległoboku o bokach 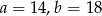 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 14 B) 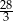 C)
C) 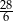 D) 5
D) 5
W równoległoboku o bokach 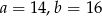 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 21 B) 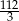 C)
C) 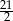 D)
D) 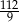
W równoległoboku 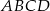 mamy dane
mamy dane 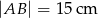 i
i 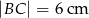 . Jedna z wysokości tego równoległoboku ma długość
. Jedna z wysokości tego równoległoboku ma długość 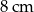 . Zatem druga wysokość ma długość
. Zatem druga wysokość ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
W równoległoboku o bokach 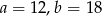 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 8 B) 12 C) 9 D) 4
Sinus kąta ostrego równoległoboku jest równy  . Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
. Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
A) 0 B) 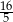 C)
C) 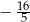 D)
D) 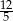
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 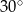 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 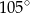 B)
B) 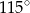 C)
C) 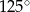 D)
D) 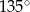
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 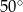 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 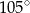 B)
B) 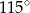 C)
C) 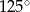 D)
D) 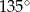
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 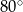 . Kąt rozwarty tego równoległoboku ma miarę
. Kąt rozwarty tego równoległoboku ma miarę
A) 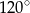 B)
B) 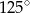 C)
C) 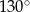 D)
D) 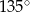
Dwa sąsiednie kąty równoległoboku różnią się o 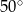 . Kąt ostry tego równoległoboku ma miarę
. Kąt ostry tego równoległoboku ma miarę
A) 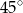 B)
B) 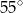 C)
C) 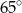 D)
D) 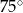
Boki równoległoboku 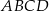 mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
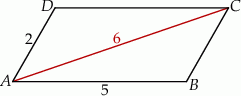
Pole tego równoległoboku jest równe
A) 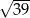 B) 48 C)
B) 48 C) 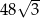 D)
D) 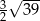
Przekątne podzieliły równoległobok na cztery trójkąty o polach 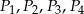 .
.
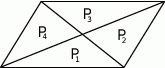
Który z podanych warunków może nie być spełniony?
A) 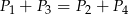 B)
B) 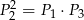 C)
C) 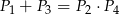 D)
D)