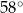Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 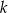 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 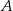 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 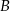 (zobacz rysunek).
(zobacz rysunek).
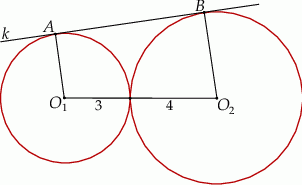
Długość odcinka 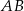 jest równa
jest równa
A) 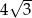 B) 7 C) 6 D)
B) 7 C) 6 D) 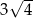
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 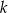 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 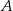 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 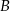 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 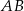 jest równa
jest równa
A) 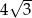 B) 7 C) 6 D)
B) 7 C) 6 D) 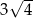
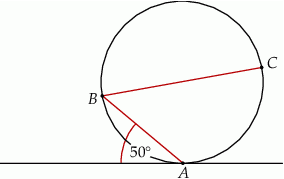
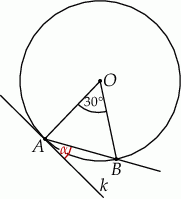
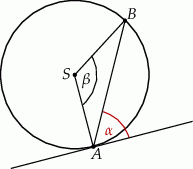
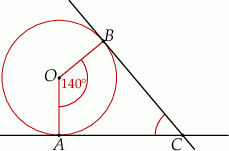
Punkt 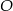 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę
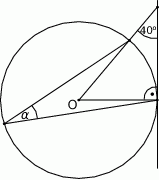
A) 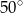 B)
B) 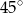 C)
C) 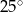 D)
D) 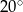
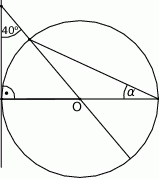
Punkt 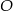 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę
A) 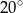 B)
B) 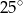 C)
C) 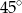 D)
D) 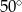
Przez wierzchołek 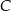 trójkąta prostokątnego
trójkąta prostokątnego 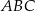 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
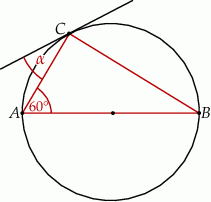
Jeżeli 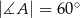 to miara kąta
to miara kąta  jest równa
jest równa
A) 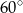 B)
B) 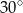 C)
C) 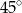 D)
D) 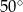
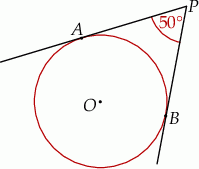
Dane są okrąg i prosta styczna do tego okręgu w punkcie 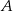 . Punkty
. Punkty 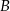 i
i 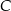 są położone na okręgu tak, że
są położone na okręgu tak, że 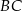 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 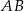 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 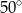 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 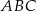 jest równa
jest równa
A) 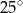 B)
B) 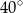 C)
C) 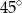 D)
D) 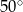
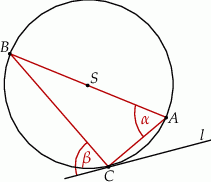
Prosta 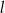 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 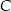 . Jeżeli kąt
. Jeżeli kąt 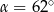 , to miara kąta
, to miara kąta 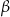 jest równa
jest równa
A) 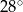 B)
B) 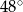 C)
C) 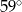 D)
D) 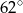
Przez wierzchołek 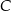 trójkąta prostokątnego
trójkąta prostokątnego 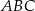 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
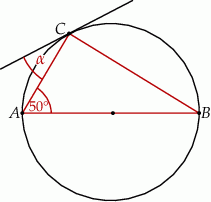
Jeżeli 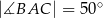 to miara kąta
to miara kąta  jest równa
jest równa
A) 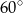 B)
B) 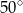 C)
C) 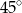 D)
D) 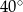
Dane są okrąg i prosta styczna do tego okręgu w punkcie 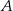 . Punkty
. Punkty 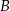 i
i 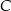 są położone na okręgu tak, że
są położone na okręgu tak, że 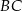 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 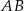 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 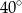 (zobacz rysunek).
(zobacz rysunek).
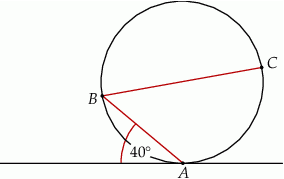
Miara kąta 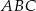 jest równa
jest równa
A) 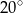 B)
B) 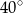 C)
C) 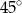 D)
D) 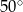
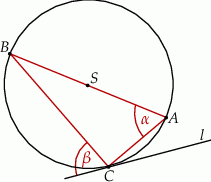
Prosta 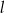 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 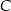 . Jeżeli kąt
. Jeżeli kąt 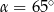 , to miara kąta
, to miara kąta 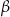 jest równa
jest równa
A) 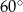 B)
B) 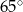 C)
C) 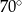 D)
D) 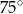
Prosta 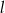 jest styczna do okręgu o środku
jest styczna do okręgu o środku 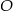 w punkcie
w punkcie 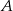 ,
, 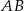 jest cięciwą okręgu,
jest cięciwą okręgu, 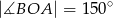 . Wówczas kąt ostry
. Wówczas kąt ostry  między cięciwą
między cięciwą 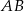 , a prostą
, a prostą 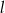 jest równy
jest równy
A) 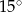 B)
B) 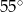 C)
C) 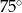 D)
D) 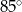
W okręgu o środku w punkcie 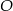 poprowadzono cięciwę
poprowadzono cięciwę 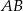 . Trójkąt
. Trójkąt 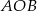 jest prostokątny. Miara kąta, jaki tworzy cięciwa
jest prostokątny. Miara kąta, jaki tworzy cięciwa 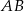 ze styczną do okręgu poprowadzoną w punkcie
ze styczną do okręgu poprowadzoną w punkcie 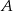 , jest równa
, jest równa
A) 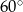 B)
B) 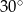 C)
C) 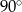 D)
D) 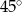
Okręgi o promieniach 4 cm oraz 6 cm są styczne zewnętrznie. Prosta, która jest styczna do okręgu o promieniu 6 cm w punkcie 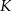 przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
przechodzi przez środek okręgu o promieniu 4 cm (patrz rysunek).
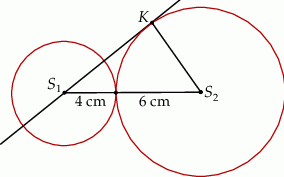
Długość odcinka 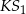 jest równa
jest równa
A) 6 cm B) 8 cm C) 10 cm D) 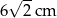
Dany jest okrąg o środku w punkcie 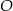 . Prosta
. Prosta 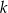 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 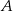 .
.
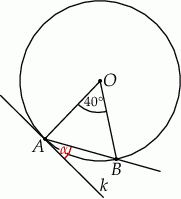
Miara kąta 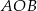 wynosi
wynosi 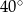 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 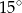 B)
B) 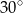 C)
C) 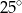 D)
D) 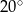
W okręgu o środku 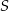 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 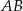 . Przez punkt
. Przez punkt 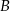 poprowadzono prostą
poprowadzono prostą 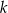 styczną do okręgu.
styczną do okręgu.
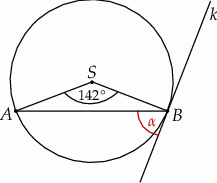
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną 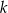 i cięciwą
i cięciwą 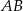 ma miarę
ma miarę
A) 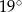 B)
B) 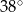 C)
C) 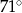 D)
D) 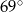
Dany jest okrąg o środku w punkcie 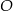 . Prosta
. Prosta 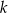 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 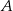 .
.
Miara kąta 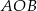 wynosi
wynosi 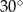 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 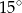 B)
B) 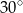 C)
C) 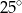 D)
D) 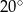
Dany jest okrąg o środku w punkcie  . Prosta
. Prosta 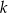 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 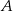 .
.
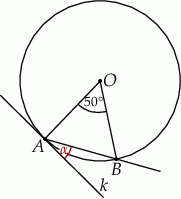
Miara kąta 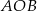 wynosi
wynosi 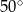 . Wobec tego miara kąta
. Wobec tego miara kąta  jest równa
jest równa
A) 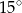 B)
B) 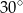 C)
C) 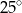 D)
D) 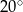
Punkty 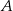 oraz
oraz 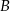 leżą na okręgu o środku
leżą na okręgu o środku 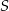 . Kąt środkowy
. Kąt środkowy 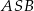 ma miarę
ma miarę 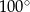 . Prosta
. Prosta 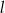 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 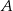 i tworzy z cięciwą
i tworzy z cięciwą 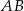 okręgu kąt o mierze
okręgu kąt o mierze  (zobacz rysunek).
(zobacz rysunek).
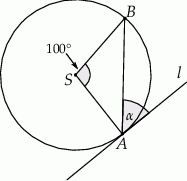
Wtedy
A) 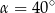 B)
B) 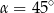 C)
C) 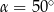 D)
D) 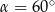
W okręgu o środku 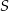 zaznaczono kąt oparty na łuku
zaznaczono kąt oparty na łuku 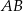 . Przez punkt
. Przez punkt  poprowadzono prostą
poprowadzono prostą  styczną do okręgu.
styczną do okręgu.
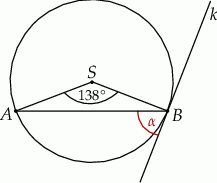
Zaznaczony na rysunku kąt  zawarty między styczną
zawarty między styczną  i cięciwą
i cięciwą 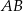 ma miarę
ma miarę
A) 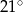 B)
B) 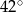 C)
C) 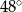 D)
D) 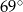
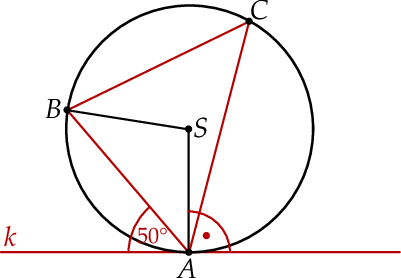
Dane są okrąg o środku 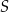 oraz prosta
oraz prosta 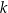 styczna do okręgu w punkcie
styczna do okręgu w punkcie 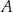 . Odcinek
. Odcinek 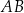 jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą
jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą 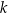 a cięciwą
a cięciwą 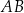 jest równa
jest równa 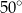 . Punkt
. Punkt 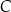 leży na okręgu. Kąt wpisany
leży na okręgu. Kąt wpisany 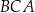 jest ostry.
jest ostry.
Miara kąta wpisanego 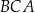 jest równa
jest równa
A) 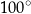 B)
B) 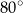 C)
C) 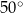 D)
D) 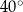
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
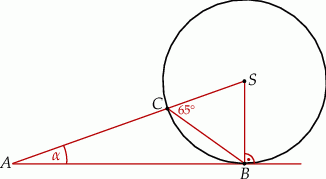
A) 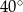 B)
B) 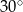 C)
C) 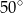 D)
D) 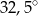
Prosta 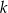 jest styczna w punkcie
jest styczna w punkcie 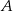 do okręgu o środku
do okręgu o środku 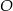 . Punkt
. Punkt 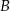 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 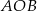 jest równa
jest równa 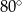 . Przez punkty
. Przez punkty 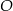 i
i 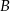 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 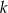 w punkcie
w punkcie 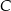 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 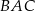 jest równa
jest równa
A) 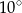 B)
B) 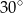 C)
C) 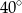 D)
D) 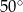
Prosta 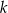 jest styczna w punkcie
jest styczna w punkcie 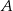 do okręgu o środku
do okręgu o środku 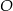 . Punkt
. Punkt 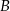 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 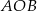 jest równa
jest równa 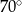 . Przez punkty
. Przez punkty 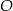 i
i 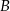 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 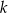 w punkcie
w punkcie 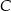 (zobacz rysunek).
(zobacz rysunek).
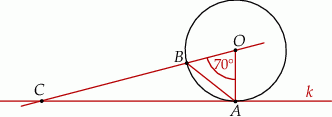
Miara kąta 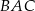 jest równa
jest równa
A) 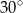 B)
B) 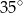 C)
C) 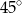 D)
D) 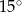
Kąt między cięciwą 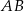 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 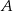 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 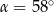 . Wówczas
. Wówczas
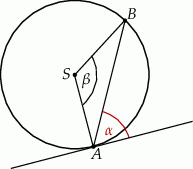
A) 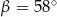 B)
B) 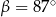 C)
C) 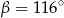 D)
D) 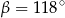
Punkty 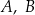 oraz
oraz 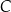 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 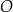 . Prosta
. Prosta 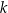 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 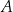 i tworzy z cięciwą
i tworzy z cięciwą 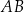 kąt o mierze
kąt o mierze 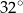 . Ponadto odcinek
. Ponadto odcinek 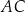 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 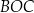 jest równa
jest równa
A) 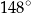 B)
B) 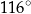 C)
C) 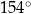 D)
D) 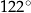
Kąt między cięciwą 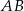 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 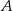 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 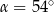 . Wówczas
. Wówczas
A) 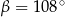 B)
B) 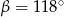 C)
C) 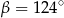 D)
D) 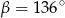
Punkty 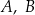 oraz
oraz 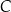 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 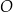 . Prosta
. Prosta 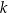 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 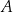 i tworzy z cięciwą
i tworzy z cięciwą 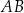 kąt o mierze
kąt o mierze 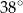 . Ponadto odcinek
. Ponadto odcinek 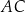 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 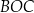 jest równa
jest równa
A) 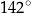 B)
B) 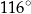 C)
C) 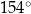 D)
D) 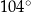
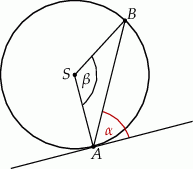
Kąt między cięciwą 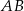 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 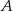 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 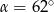 . Wówczas
. Wówczas
A) 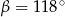 B)
B) 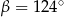 C)
C) 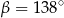 D)
D) 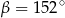
Na trójkącie 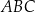 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 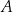 (zobacz rysunek obok).
(zobacz rysunek obok).
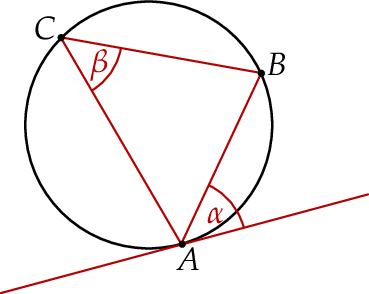
Jeżeli 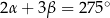 , to
, to
A) 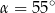 B)
B) 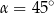 C)
C) 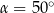 D)
D) 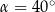
Okrąg o środku 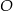 jest styczny do prostej
jest styczny do prostej 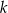 w punkcie
w punkcie 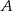 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 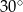 B)
B) 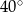 C)
C) 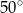 D)
D) 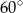
Okrąg o środku 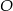 jest styczny do prostej
jest styczny do prostej 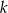 w punkcie
w punkcie  .
.
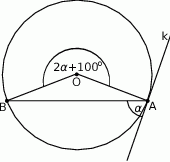
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 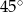 B)
B) 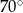 C)
C) 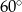 D)
D) 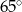
Okrąg o środku 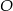 jest styczny do prostej
jest styczny do prostej 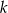 w punkcie
w punkcie  .
.
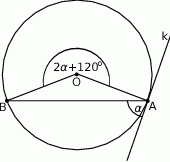
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 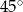 B)
B) 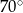 C)
C) 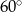 D)
D) 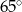
Okrąg o środku 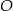 jest styczny do prostej
jest styczny do prostej 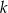 w punkcie
w punkcie 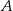 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 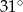 B)
B) 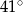 C)
C) 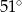 D)
D) 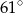
Okrąg o środku 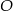 jest styczny do prostej
jest styczny do prostej 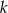 w punkcie
w punkcie 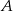 .
.
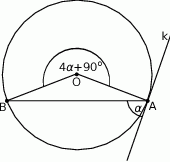
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 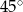 B)
B) 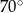 C)
C) 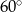 D)
D) 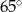
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 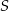 wynosi
wynosi
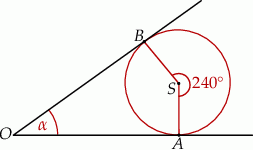
A) 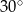 B)
B) 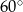 C)
C) 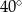 D)
D) 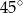
Przez punkty 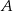 i
i 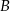 , leżące na okręgu o środku
, leżące na okręgu o środku 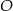 , poprowadzono proste styczne do tego okręgu, przecinające się w punkcie
, poprowadzono proste styczne do tego okręgu, przecinające się w punkcie 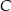 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 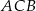 jest równa
jest równa
A) 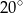 B)
B) 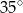 C)
C) 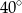 D)
D) 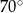
Do okręgu o środku 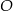 poprowadzono z zewnętrznego punktu
poprowadzono z zewnętrznego punktu 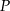 dwie styczne przecinające się w
dwie styczne przecinające się w 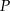 pod kątem
pod kątem 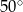 (zobacz rysunek). Punktami styczności są, odpowiednio, punkty
(zobacz rysunek). Punktami styczności są, odpowiednio, punkty 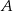 i
i 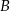 .
.
Kąt 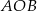 ma miarę
ma miarę
A) 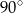 B)
B) 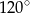 C)
C) 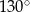 D)
D) 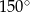
Punkty 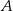 oraz
oraz 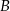 leżą na okręgu o środku
leżą na okręgu o środku 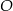 . Proste
. Proste 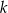 i
i 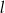 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 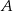 i
i 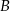 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 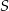 i tworzą kąt o mierze
i tworzą kąt o mierze 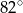 (zobacz rysunek).
(zobacz rysunek).
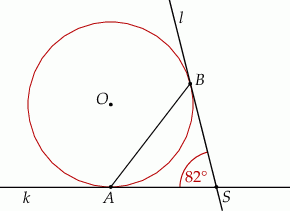
Miara kąta 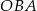 jest równa
jest równa
A) 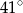 B)
B) 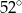 C)
C) 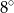 D)
D) 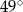
Punkty 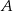 oraz
oraz 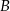 leżą na okręgu o środku
leżą na okręgu o środku 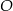 . Proste
. Proste 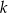 i
i 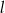 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 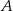 i
i 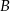 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 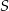 i tworzą kąt o mierze
i tworzą kąt o mierze 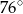 (zobacz rysunek).
(zobacz rysunek).
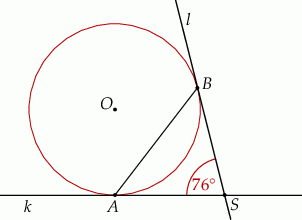
Miara kąta 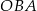 jest równa
jest równa
A) 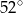 B)
B) 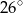 C)
C) 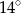 D)
D) 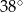
Na rysunku prosta 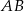 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 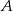 . Punkt
. Punkt 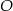 jest środkiem okręgu.
jest środkiem okręgu.
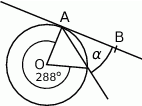
Kąt dopisany  ma miarę:
ma miarę:
A) 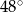 B)
B) 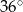 C)
C) 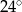 D)
D) 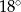
Na rysunku prosta 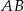 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 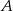 . Punkt
. Punkt 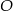 jest środkiem okręgu.
jest środkiem okręgu.
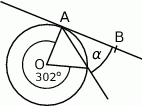
Kąt dopisany  ma miarę:
ma miarę:
A) 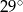 B)
B) 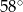 C)
C) 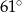 D)
D) 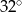
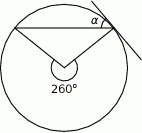
Prosta jest styczna do okręgu. Kąt  (patrz rysunek) ma miarę:
(patrz rysunek) ma miarę:
A) 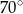 B)
B) 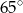 C)
C) 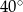 D)
D) 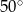
Na rysunku przedstawiono okrąg o środku 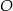 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 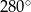 . Punkty
. Punkty 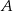 i
i 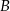 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta 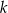 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 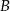 .
.
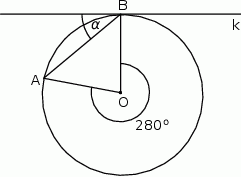
Miara kąta  jest równa
jest równa
A) 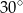 B)
B) 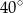 C)
C) 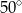 D)
D) 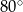
Na rysunku przedstawiono okrąg o środku 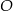 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 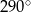 . Punkty
. Punkty 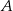 i
i 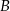 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta  jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie  .
.
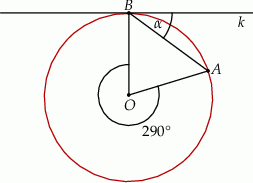
Miara kąta  jest równa
jest równa
A) 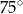 B)
B) 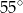 C)
C) 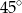 D)
D) 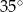
Na rysunku prosta 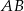 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 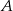 . Punkt
. Punkt 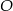 jest środkiem okręgu.
jest środkiem okręgu.
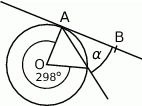
Kąt dopisany  ma miarę:
ma miarę:
A) 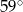 B)
B) 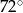 C)
C) 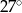 D)
D) 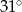
Punkty 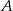 ,
, 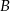 i
i 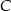 leżą na okręgu o środku
leżą na okręgu o środku 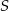 , a prosta
, a prosta 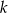 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 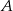 .
.
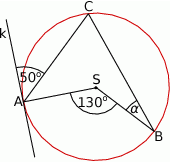
Zaznaczony na rysunku kąt  zawarty między promieniem
zawarty między promieniem 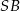 i cięciwą
i cięciwą 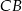 ma miarę
ma miarę
A) 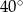 B)
B) 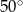 C)
C) 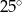 D)
D) 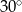
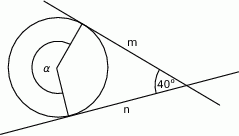
Proste 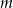 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 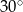 .
.
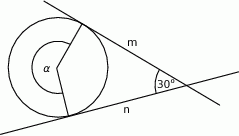
Miara kąta  jest równa
jest równa
A) 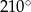 B)
B) 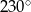 C)
C) 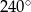 D)
D) 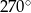
Proste 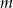 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 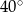 .
.
Miara kąta  jest równa
jest równa
A) 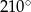 B)
B) 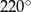 C)
C) 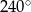 D)
D) 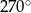
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 4 w punkcie 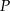 przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
przechodzi przez środek okręgu o promieniu 3 (zobacz rysunek).
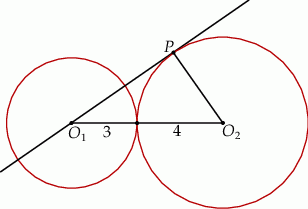
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności P, jest równe
A) 14 B) 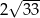 C)
C) 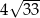 D) 12
D) 12
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 3 w punkcie 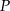 przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
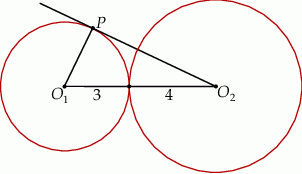
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności 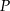 , jest równe
, jest równe
A) 21 B) 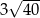 C)
C) 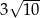 D) 24
D) 24
Prosta 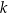 jest styczna w punkcie
jest styczna w punkcie 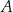 do okręgu opisanego na trójkącie równoramiennym
do okręgu opisanego na trójkącie równoramiennym 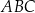 , w którym
, w którym 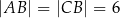 . Prosta
. Prosta 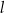 zawiera punkty
zawiera punkty 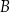 i
i 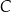 i przecina prostą
i przecina prostą 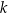 w punkcie
w punkcie 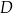 , przy czym
, przy czym 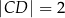 i
i 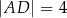 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 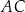 jest równa
jest równa
A) 3 B)  C)
C) 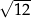 D)
D) 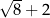
Odcinek 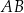 jest średnicą okręgu o środku
jest średnicą okręgu o środku 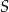 . Prosta
. Prosta 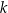 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 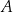 . Prosta
. Prosta 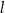 przecina ten okrąg w punktach
przecina ten okrąg w punktach 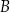 i
i 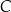 . Proste
. Proste 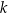 i
i 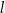 przecinają się w punkcie
przecinają się w punkcie 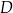 , przy czym
, przy czym 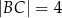 i
i 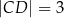 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 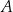 od prostej
od prostej 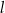 jest równa
jest równa
A) 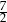 B) 5 C)
B) 5 C) 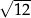 D)
D) 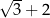
Odcinek 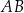 jest średnicą okręgu o środku
jest średnicą okręgu o środku 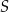 . Prosta
. Prosta 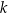 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 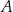 . Prosta
. Prosta 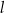 przecina ten okrąg w punktach
przecina ten okrąg w punktach 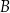 i
i 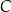 . Proste
. Proste 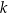 i
i 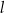 przecinają się w punkcie
przecinają się w punkcie 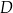 , przy czym
, przy czym 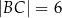 i
i 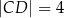 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 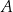 od prostej
od prostej 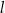 jest równa
jest równa
A) 8 B) 5 C) 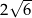 D)
D) 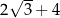
Prostokąt 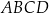 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 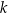 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 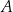 i tworzy z odcinkiem
i tworzy z odcinkiem 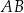 kąt o mierze
kąt o mierze  . Przekątne prostokąta
. Przekątne prostokąta 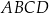 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze 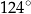 (zobacz rysunek).
(zobacz rysunek).
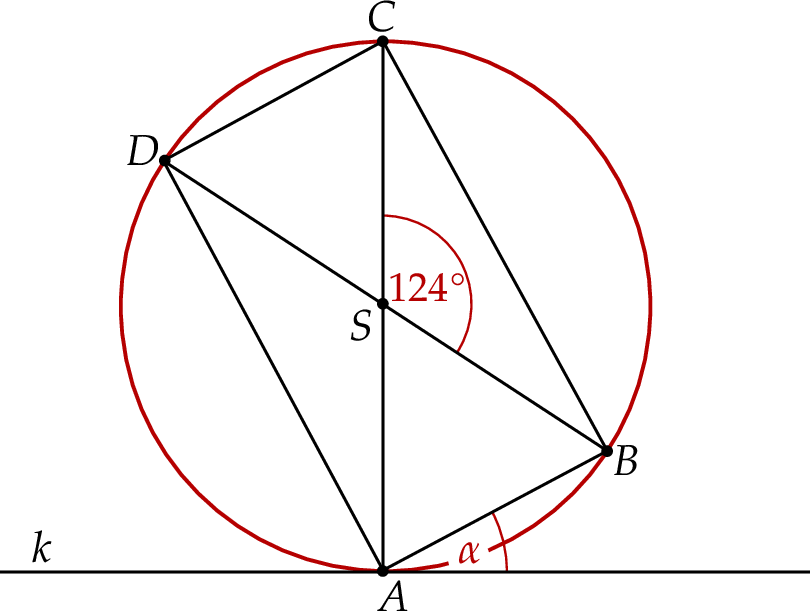
Miara kąta  jest równa
jest równa
A) 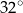 B)
B) 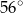 C)
C) 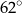 D)
D) 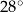
Odcinek 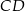 jest wysokością trójkąta
jest wysokością trójkąta 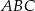 , w którym
, w którym 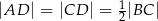 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 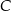 i promieniu
i promieniu 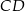 jest styczny do prostej
jest styczny do prostej 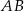 . Okrąg ten przecina boki
. Okrąg ten przecina boki 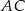 i
i 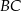 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 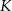 i
i 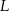 .
.
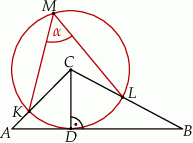
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 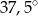 B)
B) 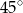 C)
C) 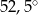 D)
D) 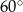
Odcinek 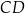 jest wysokością trójkąta równoramiennego
jest wysokością trójkąta równoramiennego 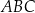 , w którym
, w którym 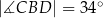 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 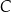 i promieniu
i promieniu 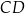 jest styczny do prostej
jest styczny do prostej 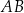 . Okrąg ten przecina boki
. Okrąg ten przecina boki 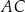 i
i 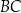 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 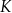 i
i 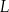 .
.

Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 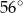 B)
B) 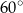 C)
C)  D)
D)