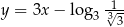Proste prostopadłe 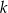 i
i 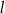 o równaniach
o równaniach 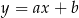 oraz
oraz 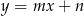 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 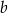 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 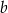 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 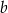 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 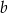 i
i  muszą być dodatnie
muszą być dodatnie
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Proste prostopadłe
Prosta o równaniu 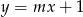 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 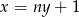 . Stąd wynika, że
. Stąd wynika, że
A) 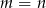 B)
B) 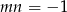 C)
C) 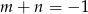 D)
D) 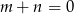
Prosta o równaniu 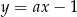 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 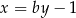 . Stąd wynika, że
. Stąd wynika, że
A) 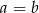 B)
B) 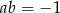 C)
C) 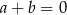 D)
D) 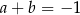
Prosta 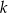 przechodzi przez punkt
przechodzi przez punkt 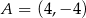 i jest prostopadła do osi
i jest prostopadła do osi 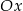 . Prosta
. Prosta 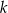 ma równanie
ma równanie
A) 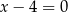 B)
B) 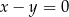 C)
C) 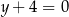 D)
D) 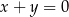
Prosta 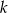 przechodzi przez punkt
przechodzi przez punkt 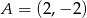 i jest prostopadła do osi
i jest prostopadła do osi 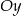 . Prosta
. Prosta 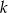 ma równanie
ma równanie
A) 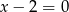 B)
B) 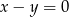 C)
C) 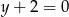 D)
D) 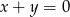
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 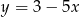 jest równy
jest równy
A) 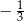 B) 3 C) -5 D)
B) 3 C) -5 D) 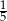
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 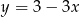 jest równy
jest równy
A) 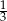 B) 3 C) -3 D)
B) 3 C) -3 D) 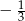
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 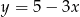 jest równy
jest równy
A) 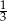 B) -3 C) 5 D)
B) -3 C) 5 D) 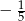
Prosta 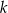 ma równanie
ma równanie 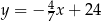 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 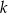 jest równy
jest równy
A)  B)
B) 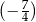 C)
C) 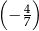 D)
D) 
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 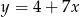 jest równy
jest równy
A) 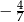 B)
B) 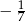 C) 7 D)
C) 7 D) 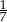
Prosta przechodząca przez punkt 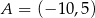 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 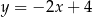 B)
B) 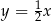 C)
C) 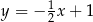 D)
D) 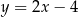
Prosta przechodząca przez punkt 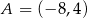 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 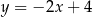 B)
B) 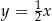 C)
C) 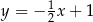 D)
D) 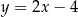
Prosta przechodząca przez punkt 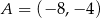 i początek układu współrzędnych jest prostopadła do prostej o równaniu
i początek układu współrzędnych jest prostopadła do prostej o równaniu
A) 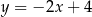 B)
B) 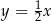 C)
C) 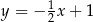 D)
D) 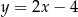
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 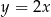 i
i 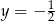 B)
B) 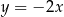 i
i 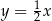
C) 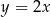 i
i 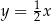 D)
D) 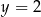 i
i 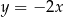
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 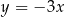 i
i 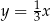 B)
B) 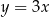 i
i 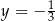
C) 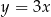 i
i 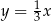 D)
D) 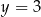 i
i 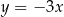
Liczba różnych wartości parametru  , dla których prosta
, dla których prosta 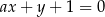 jest prostopadła do prostej
jest prostopadła do prostej 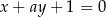 jest
jest
A) równa 0 B) równa 1 C) równa 2 D) większa od 2
Prosta prostopadła do prostej 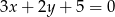 ma równanie:
ma równanie:
A) 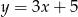 B)
B) 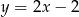 C)
C) 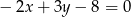 D)
D) 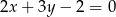
Dana jest prosta 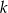 o równaniu
o równaniu 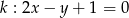 . Spośród podanych prostych wybierz prostą prostopadłą do
. Spośród podanych prostych wybierz prostą prostopadłą do 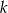 .
.
A) 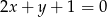 B)
B) 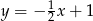 C)
C) 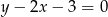 D)
D) 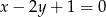
Prostą prostopadłą do prostej o równaniu 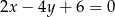 jest prosta o równaniu
jest prosta o równaniu
A) 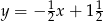 B)
B) 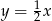 C)
C) 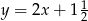 D)
D) 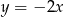
Prosta prostopadła do prostej 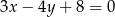 ma równanie:
ma równanie:
A) 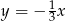 B)
B) 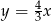 C)
C) 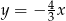 D)
D) 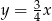
Wskaż równanie prostej prostopadłej do prostej o równaniu 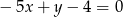 .
.
A) 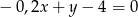 B)
B) 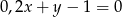 C)
C) 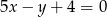 D)
D) 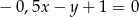
Prostą prostopadłą do prostej o równaniu 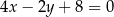 jest prosta o równaniu
jest prosta o równaniu
A) 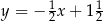 B)
B) 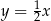 C)
C) 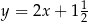 D)
D) 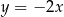
Prosta 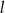 ma równanie
ma równanie 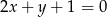 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do  .
.
A) 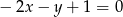 B)
B) 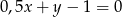 C)
C) 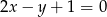 D)
D) 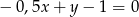
Prosta prostopadła do prostej 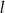 o równaniu
o równaniu 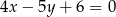 ma wzór
ma wzór
A) 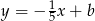 B)
B) 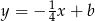 C)
C) 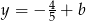 D)
D) 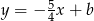
Proste o równaniach: 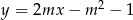 oraz
oraz 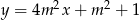 są prostopadłe dla
są prostopadłe dla
A) 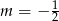 B)
B) 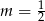 C)
C) 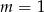 D)
D) 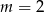
Proste opisane równaniami 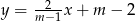 oraz
oraz 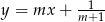 są prostopadłe, gdy
są prostopadłe, gdy
A) 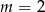 B)
B) 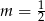 C)
C) 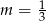 D)
D) 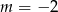
Proste opisane równaniami 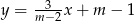 oraz
oraz 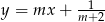 są prostopadłe, gdy
są prostopadłe, gdy
A) 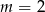 B)
B) 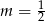 C)
C) 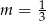 D)
D) 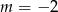
Proste o równaniach 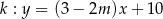 i
i 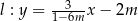 są prostopadłe dla
są prostopadłe dla
A) 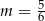 B)
B) 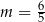 C)
C) 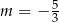 D)
D) 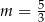
Proste o równaniach: 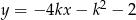 oraz
oraz 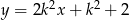 są prostopadłe dla
są prostopadłe dla
A) 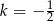 B)
B) 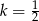 C)
C) 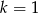 D)
D) 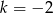
Prosta o równaniu 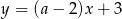 jest prostopadła do prostej
jest prostopadła do prostej 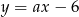 . Zatem
. Zatem
A) 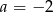 B)
B) 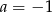 C)
C) 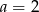 D)
D) 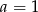
Na rysunku przedstawione są dwie proste równoległe 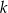 i
i 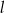 o równaniach
o równaniach 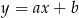 oraz
oraz 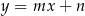 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
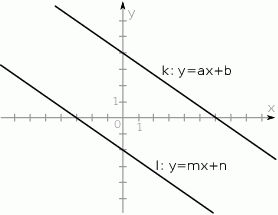
Zatem
A) 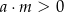 i
i 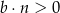 B)
B) 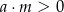 i
i 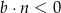
C) 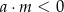 i
i 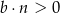 D)
D) 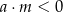 i
i 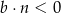
Na rysunku przedstawione są dwie proste równoległe 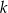 i
i 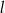 o równaniach
o równaniach 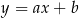 oraz
oraz 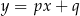 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
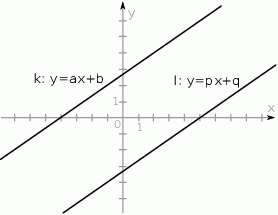
Zatem
A) 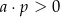 i
i 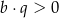 B)
B) 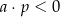 i
i 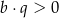
C) 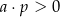 i
i 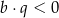 D)
D) 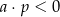 i
i 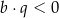
Prosta prostopadła do prostej 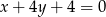 i przechodząca przez początek układu współrzędnych ma równanie
i przechodząca przez początek układu współrzędnych ma równanie
A) 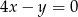 B)
B) 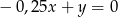 C)
C) 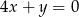 D)
D) 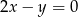
Wskaż równanie prostej przechodzącej przez początek układu współrzędnych i prostopadłej do prostej o równaniu 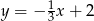 .
.
A) 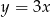 B)
B) 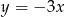 C)
C) 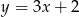 D)
D) 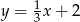
Prosta prostopadła do prostej 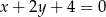 i przechodząca przez początek układu współrzędnych ma równanie
i przechodząca przez początek układu współrzędnych ma równanie
A) 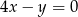 B)
B) 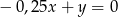 C)
C) 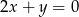 D)
D) 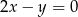
Prosta prostopadła do prostej 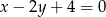 i przechodząca przez początek układu współrzędnych ma równanie
i przechodząca przez początek układu współrzędnych ma równanie
A) 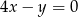 B)
B) 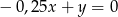 C)
C) 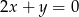 D)
D) 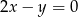
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 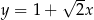 i
i 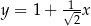 B)
B) 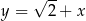 i
i 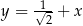
C) 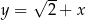 i
i 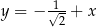 D)
D) 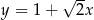 i
i 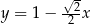
Które z równań opisuje prostą prostopadłą do prostej o równaniu 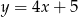 ?
?
A) 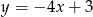 B)
B) 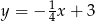 C)
C) 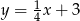 D)
D) 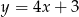
Które z równań opisuje prostą prostopadłą do prostej o równaniu 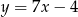 ?
?
A) 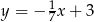 B)
B) 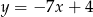 C)
C) 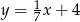 D)
D) 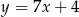
Które z równań opisuje prostą prostopadłą do prostej o równaniu 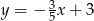 ?
?
A) 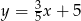 B)
B) 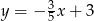 C)
C) 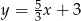 D)
D) 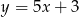
Prosta 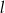 ma równanie
ma równanie 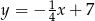 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 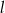 .
.
A) 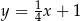 B)
B) 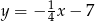 C)
C) 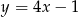 D)
D) 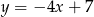
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 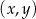 , dana jest prosta
, dana jest prosta  o równaniu
o równaniu 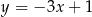 . Jedną z prostych prostopadłych do prostej
. Jedną z prostych prostopadłych do prostej 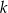 jest prosta o równaniu
jest prosta o równaniu
A) 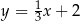 B)
B) 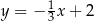 C)
C) 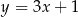 D)
D) 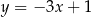
Prosta 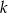 ma równanie
ma równanie 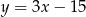 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do 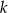 .
.
A) 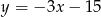 B)
B) 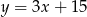 C)
C) 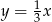 D)
D) 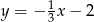
Na płaszczyźnie, w kartezjańskim układzie współrzędnych  , dana jest prosta
, dana jest prosta 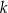 o równaniu
o równaniu 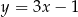 . Jedną z prostych prostopadłych do prostej
. Jedną z prostych prostopadłych do prostej 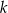 jest prosta o równaniu
jest prosta o równaniu
A) 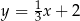 B)
B) 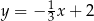 C)
C) 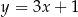 D)
D) 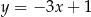
Prosta 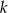 oraz prosta o równaniu
oraz prosta o równaniu 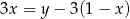 są prostopadłe oraz przecinają się w punkcie
są prostopadłe oraz przecinają się w punkcie 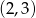 . Prosta
. Prosta 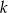 ma równanie
ma równanie
A) 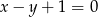 B)
B) 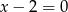 C)
C) 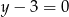 D)
D) 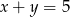
Prosta 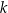 oraz prosta o równaniu
oraz prosta o równaniu 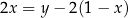 są prostopadłe oraz przecinają się w punkcie
są prostopadłe oraz przecinają się w punkcie 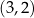 . Prosta
. Prosta 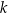 ma równanie
ma równanie
A) 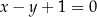 B)
B) 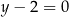 C)
C) 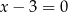 D)
D) 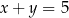
Dane są równania czterech prostych:
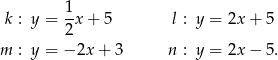
Prostopadłe są proste
A) 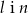 B)
B) 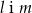 C)
C) 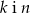 D)
D) 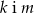
Dane są równania czterech prostych:
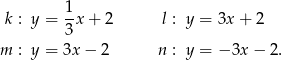
Prostopadłe są proste
A) 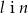 B)
B) 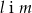 C)
C) 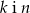 D)
D) 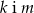
Dane są cztery proste 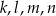 o równaniach:
o równaniach:
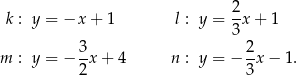
Wśród tych prostych prostopadłe są
A) proste 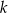 oraz
oraz 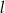 B) proste
B) proste 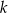 oraz
oraz 
C) proste 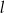 oraz
oraz 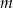 D) proste
D) proste 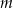 oraz
oraz 
Proste 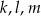 dane są równaniami
dane są równaniami 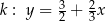 ,
, 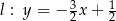 ,
, 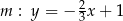 . Wynika stąd, że
. Wynika stąd, że
A) proste 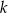 i
i 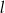 są prostopadłe
są prostopadłe
B) proste 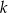 i
i 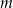 są prostopadłe
są prostopadłe
C) proste 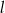 i
i 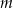 są prostopadłe
są prostopadłe
D) wśród prostych 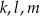 nie ma prostych prostopadłych
nie ma prostych prostopadłych
Wskaż 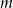 , dla którego proste
, dla którego proste 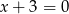 i
i 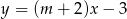 są prostopadłe.
są prostopadłe.
A) 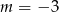 B)
B) 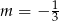 C)
C) 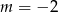 D)
D) 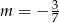
Proste o równaniach 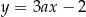 i
i 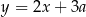 są prostopadłe. Wtedy
są prostopadłe. Wtedy  jest równe
jest równe
A)  B)
B) 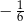 C)
C)  D)
D) 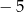
Proste 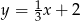 oraz
oraz 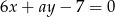 są prostopadłe, jeżeli:
są prostopadłe, jeżeli:
A) 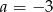 B)
B) 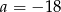 C)
C) 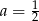 D)
D) 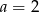
Proste 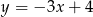 i
i 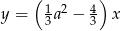 są prostopadłe, jeżeli
są prostopadłe, jeżeli
A) 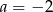 lub
lub 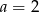 B)
B) 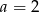 C)
C) 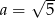 D)
D) 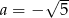 lub
lub 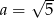
Prosta o równaniu 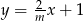 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 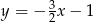 . Stąd wynika, że
. Stąd wynika, że
A) 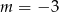 B)
B) 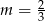 C)
C) 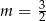 D)
D) 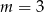
Prosta o równaniu 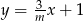 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 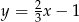 . Stąd wynika, że
. Stąd wynika, że
A) 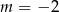 B)
B) 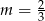 C)
C) 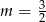 D)
D) 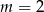
Proste o równaniach 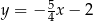 oraz
oraz 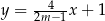 są prostopadłe. Wynika stąd, że
są prostopadłe. Wynika stąd, że
A) 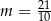 B)
B) 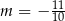 C)
C) 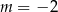 D)
D) 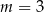
W kartezjańskim układzie współrzędnych 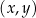 proste
proste 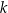 oraz
oraz 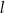 są określone równaniami
są określone równaniami
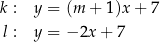
Proste 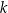 oraz
oraz 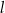 są prostopadłe, gdy liczba
są prostopadłe, gdy liczba 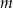 jest równa
jest równa
A) 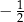 B)
B) 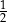 C)
C) 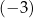 D) 1
D) 1
Proste o równaniach 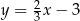 oraz
oraz 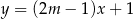 są prostopadłe, gdy
są prostopadłe, gdy
A) 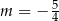 B)
B) 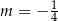 C)
C) 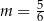 D)
D) 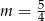
Wskaż 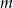 , dla którego proste
, dla którego proste 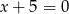 i
i 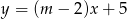 są prostopadłe.
są prostopadłe.
A) 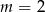 B)
B) 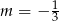 C)
C) 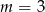 D)
D) 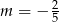
Proste o równaniach  oraz
oraz 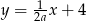 (
(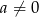 ) są prostopadłe dla
) są prostopadłe dla  równego
równego
A) 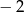 B) 2 C) 1 D)
B) 2 C) 1 D) 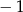
Prosta 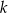 ma równanie
ma równanie 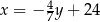 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 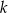 jest równy
jest równy
A)  B)
B) 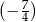 C)
C) 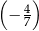 D)
D) 
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 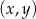 , dane są punkty
, dane są punkty 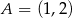 i
i 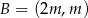 , gdzie
, gdzie 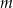 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 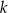 o równaniu
o równaniu 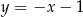 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 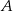 i
i 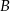 jest prostopadła do prostej
jest prostopadła do prostej 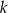 , gdy
, gdy
A) 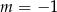 B)
B) 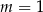 C)
C) 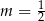 D)
D) 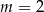
Prosta 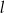 ma równanie
ma równanie 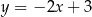 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 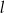 i przechodzącej przez punkt
i przechodzącej przez punkt 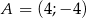 jest:
jest:
A) 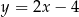 B)
B) 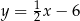 C)
C) 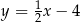 D)
D) 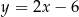
Dana jest prosta 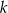 o równaniu
o równaniu 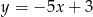 . Równanie prostej prostopadłej do prostej
. Równanie prostej prostopadłej do prostej 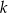 i przechodzącej przez punkt
i przechodzącej przez punkt 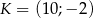 ma postać
ma postać
A) 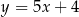 B)
B) 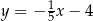 C)
C) 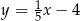 D)
D) 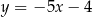
Punkt 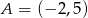 leży na prostej
leży na prostej 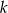 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 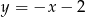 . Prosta
. Prosta 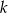 ma równanie
ma równanie
A) 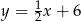 B)
B) 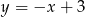 C)
C) 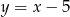 D)
D) 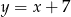
Prosta prostopadła do prostej o równaniu 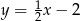 i przechodząca przez punkt
i przechodząca przez punkt 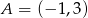 ma równanie
ma równanie
A) 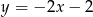 B)
B) 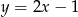 C)
C) 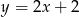 D)
D) 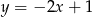
Na płaszczyźnie z układem współrzędnych proste 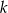 i
i 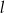 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 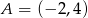 . Prosta
. Prosta 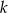 jest określona równaniem
jest określona równaniem 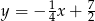 . Zatem prostą
. Zatem prostą 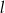 opisuje równanie
opisuje równanie
A) 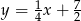 B)
B) 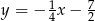 C)
C) 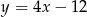 D)
D) 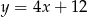
Dana jest prosta 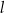 o równaniu
o równaniu 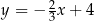 . Prosta
. Prosta 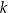 jest prostopadła do prostej
jest prostopadła do prostej 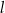 i przechodzi przez punkt
i przechodzi przez punkt 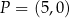 . Prosta
. Prosta 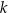 ma równanie
ma równanie
A) 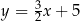 B)
B) 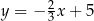 C)
C) 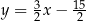 D)
D) 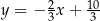
Prosta 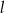 ma równanie
ma równanie 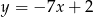 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 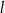 i przechodzącej przez punkt
i przechodzącej przez punkt 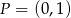 ma postać
ma postać
A) 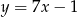 B)
B) 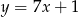 C)
C) 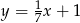 D)
D) 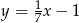
Równanie prostej prostopadłej do prostej 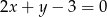 i przechodzącej przez punkt
i przechodzącej przez punkt 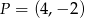 ma postać
ma postać
A) 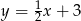 B)
B) 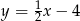 C)
C) 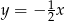 D)
D) 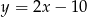
Punkt 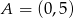 leży na prostej
leży na prostej 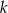 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 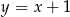 . Prosta
. Prosta 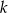 ma równanie
ma równanie
A) 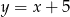 B)
B) 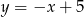 C)
C) 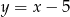 D)
D) 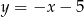
Prosta 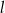 ma równanie
ma równanie 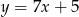 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 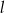 i przechodzącej przez punkt
i przechodzącej przez punkt 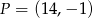 ma postać
ma postać
A) 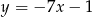 B)
B) 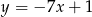 C)
C) 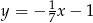 D)
D) 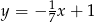
Prosta o równaniu 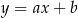 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 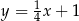 i przechodzi przez punkt
i przechodzi przez punkt 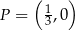 , gdy
, gdy
A) 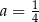 i
i 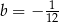 B)
B) 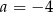 i
i 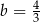
C) 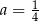 i
i 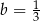 D)
D) 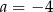 i
i 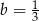
Na płaszczyźnie z układem współrzędnych proste 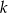 i
i 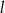 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 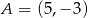 . Prosta
. Prosta 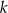 jest określona równaniem
jest określona równaniem 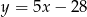 . Zatem prostą
. Zatem prostą 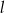 opisuje równanie
opisuje równanie
A) 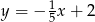 B)
B) 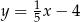 C)
C) 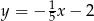 D)
D) 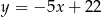
Prostą prostopadłą do prostej 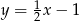 i przechodzącą przez punkt
i przechodzącą przez punkt 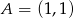 opisuje równanie:
opisuje równanie:
A) 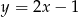 B)
B) 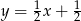 C)
C) 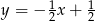 D)
D) 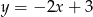
Prosta 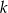 ma równanie
ma równanie 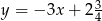 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 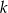 , przechodzącej przez punkt
, przechodzącej przez punkt 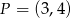 .
.
A) 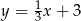 B)
B) 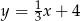 C)
C) 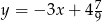 D)
D) 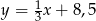
Prosta o równaniu 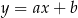 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 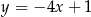 i przechodzi przez punkt
i przechodzi przez punkt 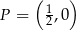 , gdy
, gdy
A) 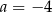 i
i 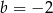 B)
B) 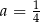 i
i 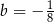
C) 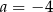 i
i 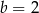 D)
D) 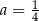 i
i 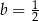
Dana jest prosta 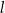 o równaniu
o równaniu 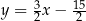 . Prosta
. Prosta 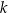 jest prostopadła do prostej
jest prostopadła do prostej 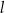 i przechodzi przez punkt
i przechodzi przez punkt 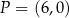 . Prosta
. Prosta 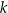 ma równanie
ma równanie
A) 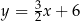 B)
B) 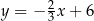 C)
C) 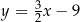 D)
D) 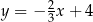
Prosta 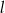 ma równanie
ma równanie 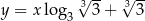 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 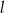 .
.
A) 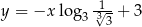 B)
B) 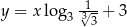
C) 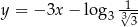 D)
D)