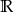Jeśli 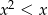 , to
, to
A) 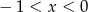 B)
B) 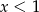 C)
C) 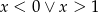 D)
D) 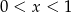
/Szkoła średnia/Zadania testowe/Nierówności/Kwadratowe/Zbiór rozwiązań
Jeśli 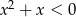 , to
, to
A) 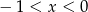 B)
B) 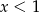 C)
C) 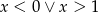 D)
D) 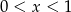
Jeśli 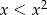 , to
, to
A) 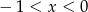 B)
B) 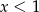 C)
C) 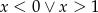 D)
D) 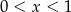
Zbiór rozwiązań nierówności kwadratowej 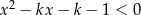 z niewiadomą
z niewiadomą  i parametrem
i parametrem 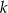 , jest taki sam jak zbiór rozwiązań nierówności
, jest taki sam jak zbiór rozwiązań nierówności 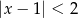 . Liczba
. Liczba 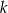 jest równa
jest równa
A) 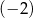 B) 2 C)
B) 2 C) 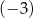 D) 3
D) 3
Przedział 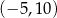 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 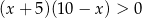 B)
B) 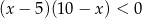
C) 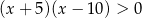 D)
D) 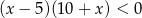
Przedział 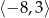 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 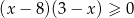 B)
B) 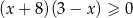
C) 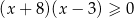 D)
D) 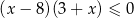
Zbiór 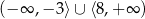 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności
A) 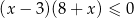 B)
B) 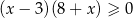
C) 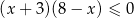 D)
D) 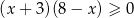
Zbiór 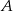 jest zbiorem wszystkich argumentów, dla których funkcja
jest zbiorem wszystkich argumentów, dla których funkcja 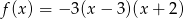 przyjmuje wartości nieujemne. Zatem
przyjmuje wartości nieujemne. Zatem
A) 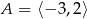 B)
B) 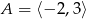 C)
C) 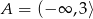 D)
D) 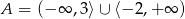
Dla jakich argumentów funkcja 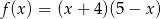 przyjmuje wartości nieujemne?
przyjmuje wartości nieujemne?
A) 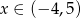 B)
B) 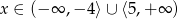 C)
C) 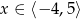 D)
D) 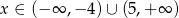
Zbiór 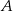 jest zbiorem wszystkich argumentów, dla których funkcja
jest zbiorem wszystkich argumentów, dla których funkcja 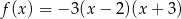 przyjmuje wartości niedodatnie. Zatem
przyjmuje wartości niedodatnie. Zatem
A) 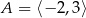 B)
B) 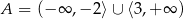
C) 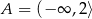 D)
D) 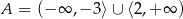
Funkcja określona wzorem 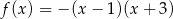 przyjmuje wartości ujemne dla
przyjmuje wartości ujemne dla
A) 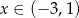 B)
B) 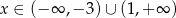
C) 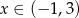 D)
D) 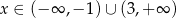
Zbiorem rozwiązań nierówności 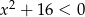 jest zbiór
jest zbiór
A) 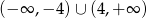 B)
B) 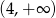 C)
C) 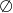 D)
D) 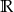
Zbiorem rozwiązań nierówności 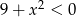 jest zbiór
jest zbiór
A) 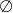 B)
B) 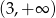 C)
C) 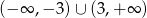 D)
D) 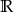
Zbiorem rozwiązań nierówności kwadratowej 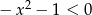 jest
jest
A) 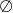 B)
B) 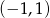 C)
C) 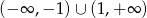 D)
D) 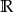
Zbiorem rozwiązań nierówności 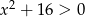 jest zbiór
jest zbiór
A) 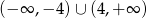 B)
B) 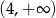 C)
C) 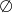 D)
D) 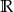
Zbiorem rozwiązań nierówności 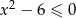 jest
jest
A) 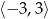 B)
B) 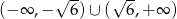 C)
C) 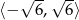 D)
D) 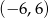
Zbiorem rozwiązań nierówności kwadratowej 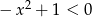 jest
jest
A) 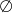 B)
B) 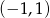 C)
C) 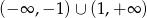 D)
D) 
Zbiorem rozwiązań nierówności 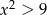 jest
jest
A) 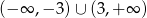 B)
B) 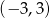 C)
C) 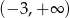 D)
D) 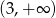
Zbiorem rozwiązań nierówności 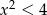 jest
jest
A) 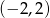 B)
B) 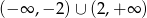 C)
C) 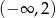 D)
D) 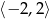
Zbiorem rozwiązań nierówności kwadratowej 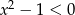 jest
jest
A) 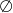 B)
B) 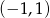 C)
C) 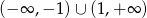 D)
D) 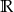
Zbiorem rozwiązań nierówności kwadratowej 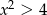 jest zbiór
jest zbiór
A) 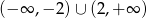 B)
B) 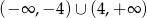 C)
C) 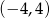 D)
D) 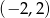
Zbiorem rozwiązań nierówności kwadratowej 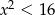 jest przedział
jest przedział
A) 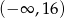 B)
B) 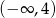 C)
C) 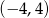 D)
D) 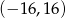
Zbiorem rozwiązań nierówności 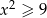 jest
jest
A) 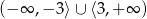 B)
B) 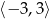 C)
C) 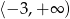 D)
D) 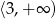
Zbiorem rozwiązań nierówności 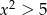 jest
jest
A) 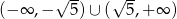 B)
B) 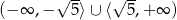 C)
C) 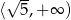 D)
D) 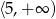
Zbiorem rozwiązań nierówności kwadratowej 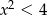 jest przedział
jest przedział
A) 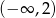 B)
B) 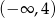 C)
C) 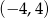 D)
D) 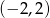
Zbiorem rozwiązań nierówności 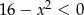 jest
jest
A) 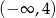 B)
B) 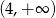 C)
C) 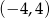 D)
D) 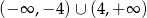
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 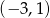 .
.
A) 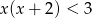 B)
B) 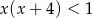 C)
C) 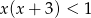 D)
D) 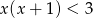
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 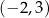 .
.
A) 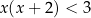 B)
B) 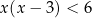 C)
C) 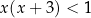 D)
D) 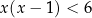
Zbiorem rozwiązań nierówności 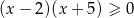 jest
jest
A) 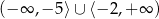 B)
B) 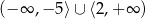
C) 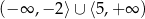 D)
D) 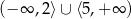
Zbiorem rozwiązań nierówności 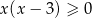 jest
jest
A) 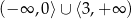 B)
B) 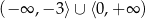
C) 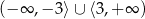 D)
D) 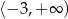
Zbiorem rozwiązań nierówności 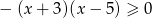 jest
jest
A) 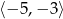 B)
B) 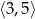 C)
C) 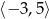 D)
D) 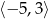
Rozwiązaniem nierówności 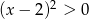 jest
jest
A) 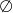 B) 2 C)
B) 2 C) 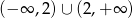 D)
D) 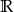
Zbiorem rozwiązań nierówności 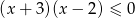 jest
jest
A) 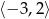 B)
B) 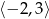 C)
C) 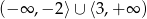 D)
D) 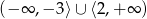
Zbiorem rozwiązań nierówności 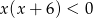 jest
jest
A) 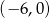 B)
B) 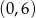 C)
C) 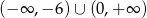 D)
D) 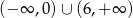
Zbiorem rozwiązań nierówności 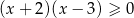 jest
jest
A) 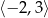 B)
B) 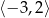
C) 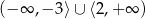 D)
D) 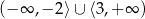
Zbiorem rozwiązań nierówności 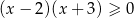 jest
jest
A) 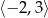 B)
B) 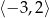
C) 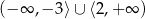 D)
D) 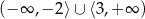
Zbiorem rozwiązań nierówności 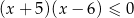 jest
jest
A) 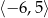 B)
B) 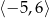
C) 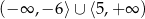 D)
D) 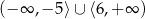
Zbiorem rozwiązań nierówności 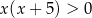 jest
jest
A) 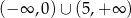 B)
B) 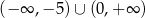
C) 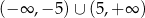 D)
D) 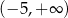
Rozwiązaniem nierówności 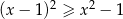 jest zbiór
jest zbiór
A) 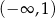 B)
B) 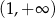 C)
C) 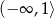 D)
D) 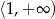
Zbiorem rozwiązań nierówności 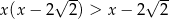 jest zbiór
jest zbiór
A) 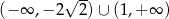 B)
B) 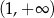
C) 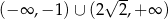 D)
D) 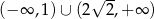
Rozwiązaniem nierówności 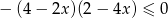 jest zbiór
jest zbiór
A) 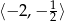 B)
B) 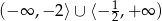 C)
C) 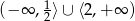 D)
D) 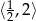
Rozwiązaniem nierówności 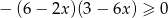 jest zbiór
jest zbiór
A) 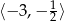 B)
B) 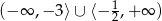 C)
C) 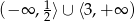 D)
D) 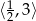
Dana jest nierówność kwadratowa
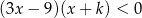
z niewiadomą  i parametrem
i parametrem 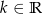 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 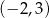 . Liczba
. Liczba 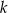 jest równa
jest równa
A) 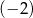 B) 2 C)
B) 2 C) 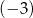 D) 3
D) 3
Dana jest nierówność kwadratowa
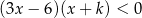
z niewiadomą  i parametrem
i parametrem 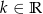 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 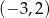 . Liczba
. Liczba 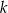 jest równa
jest równa
A) 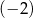 B) 2 C)
B) 2 C) 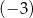 D) 3
D) 3
Rozwiązaniem nierówności 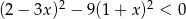 jest zbiór
jest zbiór
A) 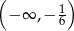 B)
B) 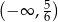 C)
C) 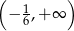 D)
D) 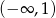
Rozwiązaniem nierówności 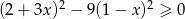 jest zbiór
jest zbiór
A) 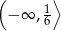 B)
B) 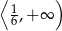 C)
C) 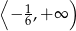 D)
D) 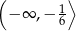
Zbiorem rozwiązań nierówności 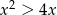 jest
jest
A) 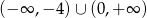 B)
B) 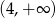 C)
C) 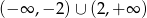 D)
D) 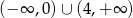
Rozwiązaniem nierówności 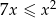 jest zbiór
jest zbiór
A) 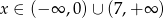 B)
B) 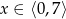 C)
C) 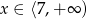 D)
D) 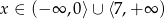
Zbiorem rozwiązań nierówności 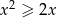 jest:
jest:
A) 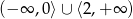 B)
B) 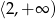 C)
C) 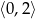 D)
D) 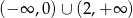
Zbiorem rozwiązań nierówności 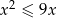 jest przedział
jest przedział
A) 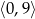 B)
B) 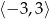 C)
C) 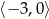 D)
D) 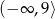
Zbiorem rozwiązań nierówności 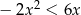 jest
jest
A) 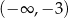 B)
B) 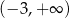 C)
C) 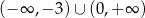 D)
D) 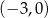
Parametr 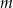 dobrano tak, że rozwiązaniem nierówności
dobrano tak, że rozwiązaniem nierówności
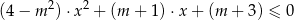
z niewiadomą  jest przedział postaci
jest przedział postaci 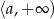 . Wynika stąd, że
. Wynika stąd, że
A) 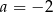 B)
B) 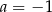 C)
C) 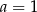 D)
D) 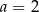
Zbiór 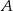 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 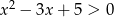 . Zatem
. Zatem
A) 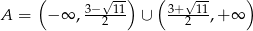 B)
B) 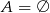 C)
C) 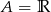 D)
D) 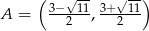
Zbiór 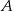 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 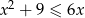 . Zatem
. Zatem
A) 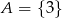 B)
B) 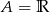 C)
C) 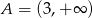 D)
D) 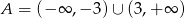
Zbiór 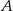 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 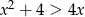 . Zatem
. Zatem
A) 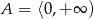 B)
B) 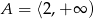 C)
C) 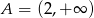 D)
D) 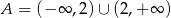
Zbiór 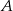 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 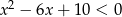 . Zatem
. Zatem
A) 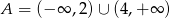 B)
B) 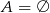 C)
C) 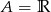 D)
D) 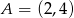
Zbiór 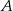 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 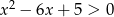 . Zatem
. Zatem
A) 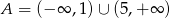 B)
B) 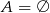 C)
C) 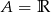 D)
D) 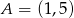
Zbiór 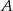 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności 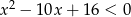 . Zatem
. Zatem
A) 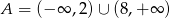 B)
B) 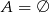 C)
C) 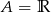 D)
D) 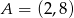
Dana jest funkcja kwadratowa 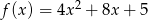 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 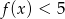 jest
jest
A) 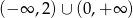 B)
B) 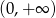 C)
C) 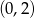 D)
D) 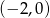
Zbiorem rozwiązań nierówności 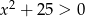 jest
jest
A) 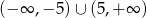 B)
B) 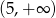 C)
C)  D)
D)