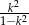Wiadomo, że 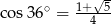 . Zatem
. Zatem
A) 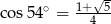 B)
B) 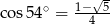 C)
C) 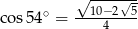 D)
D) 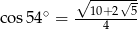
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Dany cosinus
Jeżeli 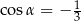 i
i  jest kątem rozwartym, to wartość
jest kątem rozwartym, to wartość 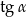 jest równa
jest równa
A) 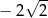 B)
B) 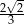 C)
C) 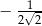 D)
D) 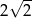
Jeśli dla kąta ostrego 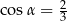 , to
, to
A) 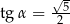 B)
B) 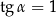 C)
C) 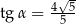 D)
D) 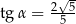
Kąt  jest ostry oraz
jest ostry oraz 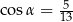 . Wtedy
. Wtedy
A) 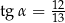 B)
B) 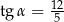 C)
C) 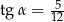 D)
D) 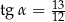
Jeśli dla kąta ostrego 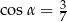 , to
, to
A) 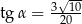 B)
B) 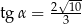 C)
C) 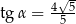 D)
D) 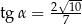
Cosinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy 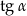 jest równy
jest równy
A) 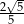 B)
B) 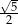 C) 2 D)
C) 2 D) 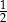
Kąt  jest ostry i
jest ostry i 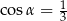 . Wobec tego
. Wobec tego
A) 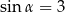 i
i 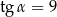 B)
B) 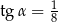 C)
C) 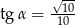 D)
D) 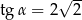
Kąt  jest ostry i
jest ostry i 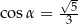 . Wobec tego
. Wobec tego
A) 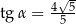 B)
B) 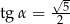 C)
C) 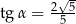 D)
D) 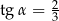
Kąt  jest ostry oraz
jest ostry oraz 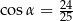 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 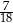 B)
B) 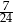 C)
C) 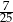 D)
D) 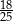
Cosinus kąta ostrego jest równy 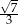 . Tangens tego kąta jest równy
. Tangens tego kąta jest równy
A) 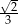 B)
B) 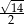 C)
C) 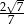 D)
D) 
Jeśli dla kąta ostrego 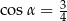 , to
, to
A) 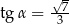 B)
B) 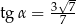 C)
C) 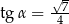 D)
D) 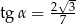
Cosinus kąta rozwartego  jest równy
jest równy 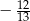 . Wtedy
. Wtedy
A) 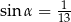 B)
B) 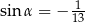 C)
C) 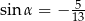 D)
D) 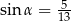
Jeżeli 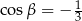 i
i 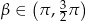 , to wartość wyrażenia
, to wartość wyrażenia 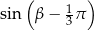 jest równa
jest równa
A) 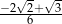 B)
B) 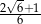 C)
C) 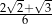 D)
D) 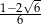
Kąt  jest ostry i
jest ostry i 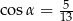 . Wtedy
. Wtedy
A) 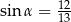 oraz
oraz 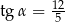 B)
B) 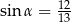 oraz
oraz 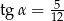
C) 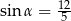 oraz
oraz 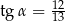 D)
D) 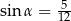 oraz
oraz 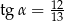
Kąt  jest ostry i
jest ostry i 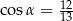 . Wtedy
. Wtedy
A) 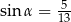 oraz
oraz 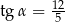 B)
B) 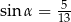 oraz
oraz 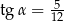
C) 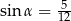 oraz
oraz 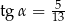 D)
D) 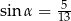 oraz
oraz 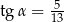
Jeśli 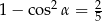 i
i  jest kątem ostrym, to
jest kątem ostrym, to 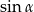 jest równy
jest równy
A) 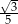 B)
B) 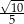 C)
C)  D)
D) 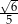
Jeżeli wiadomo, że 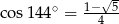 , to
, to
A) 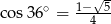 B)
B) 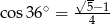 C)
C) 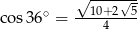 D)
D) 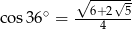
Kąt  jest ostry i
jest ostry i 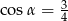 . Wtedy
. Wtedy 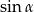 jest równy
jest równy
A) 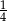 B)
B) 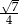 C)
C) 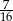 D)
D) 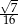
Kąt  jest ostry i
jest ostry i 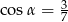 . Wtedy
. Wtedy
A) 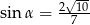 B)
B) 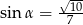 C)
C) 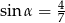 D)
D) 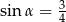
Kąt  jest ostry i
jest ostry i 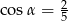 . Wtedy
. Wtedy 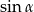 jest równy
jest równy
A) 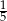 B)
B) 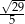 C)
C)  D)
D) 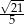
Kąt  jest ostry i
jest ostry i 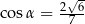 . Sinus kąta
. Sinus kąta  jest równy
jest równy
A) 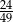 B)
B)  C)
C) 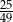 D)
D) 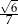
Kąt  jest ostry i
jest ostry i 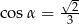 . Wtedy:
. Wtedy:
A) 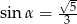 B)
B) 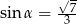 C)
C) 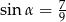 D)
D) 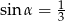
Kąt  jest ostry i
jest ostry i 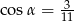 . Wówczas
. Wówczas 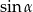 jest równy
jest równy
A) 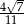 B)
B) 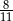 C)
C) 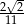 D)
D) 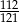
Kąt  jest ostry i
jest ostry i 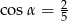 . Wówczas
. Wówczas
A) 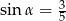 B)
B) 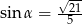 C)
C) 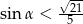 D)
D) 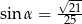
Cosinus kąta ostrego  jest równy
jest równy 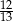 . Wtedy
. Wtedy
A) 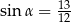 B)
B) 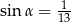 C)
C) 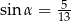 D)
D) 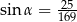
Kąt  jest ostry i
jest ostry i 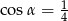 . Wtedy
. Wtedy 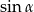 jest równy
jest równy
A) 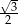 B)
B) 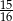 C)
C) 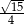 D)
D) 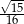
Wiadomo, że 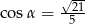 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia 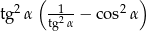 jest równa:
jest równa:
A) 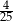 B)
B) 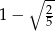 C)
C) 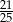 D)
D) 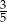
Wiadomo, że 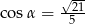 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia 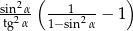 jest równa:
jest równa:
A) 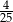 B)
B) 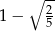 C)
C) 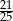 D)
D) 
Jeżeli wiadomo, że  jest kątem rozwartym i
jest kątem rozwartym i 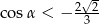 , to
, to 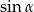 jest liczbą z przedziału
jest liczbą z przedziału
A) 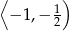 B)
B) 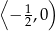 C)
C) 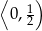 D)
D) 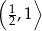
Jeśli 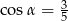 , to wartość wyrażenia
, to wartość wyrażenia 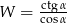 jest równa
jest równa
A) 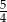 B)
B) 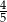 C) 1 D) 2
C) 1 D) 2
Jeśli 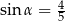 , to wartość wyrażenia
, to wartość wyrażenia 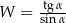 jest równa
jest równa
A) 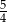 B)
B) 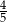 C)
C) 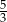 D)
D) 
Jeśli 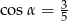 , to wartość wyrażenia
, to wartość wyrażenia 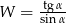 jest równa
jest równa
A) 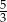 B)
B) 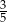 C)
C) 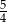 D)
D) 
Kąt  jest ostry oraz
jest ostry oraz 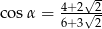 . Wtedy
. Wtedy 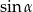 jest równy
jest równy
A) 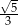 B)
B) 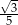 C)
C) 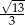 D)
D) 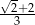
Kąt  jest ostry i
jest ostry i 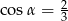 . Wartość wyrażenia
. Wartość wyrażenia 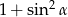 jest równa
jest równa
A) 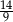 B)
B) 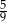 C)
C)  D)
D) 
Kąt  jest ostry i
jest ostry i 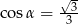 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 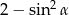 jest równa
jest równa
A) 0 B)  C)
C) 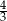 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 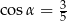 . Wtedy
. Wtedy
A) 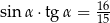 B)
B) 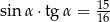 C)
C) 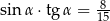 D)
D) 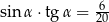
Kąt  jest ostry i
jest ostry i 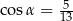 . Wtedy
. Wtedy
A) 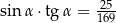 B)
B) 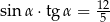 C)
C) 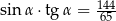 D)
D) 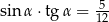
Kąt  jest ostry i
jest ostry i 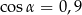 . Wówczas
. Wówczas
A) 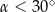 B)
B) 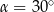 C)
C) 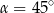 D)
D) 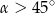
Kąt  jest ostry i
jest ostry i 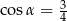 . Wówczas
. Wówczas
A) 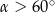 B)
B) 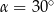 C)
C) 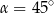 D)
D) 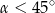
Kąt  jest kątem ostrym i
jest kątem ostrym i 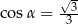 . Zatem
. Zatem
A) 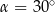 B)
B) 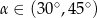 C)
C) 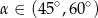 D)
D) 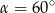
Kąt  jest ostry i
jest ostry i 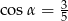 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 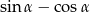 jest równa
jest równa
A) 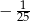 B)
B)  C)
C) 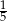 D)
D) 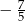
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 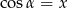 . Wtedy
. Wtedy 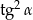 równa się
równa się
A) 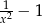 B)
B) 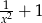 C)
C) 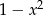 D)
D) 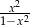
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 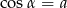 . Wtedy
. Wtedy 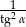 równa się
równa się
A) 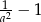 B)
B) 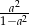 C)
C) 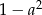 D)
D) 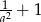
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 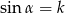 . Wtedy
. Wtedy 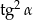 równa się
równa się
A) 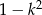 B)
B) 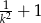 C)
C) 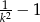 D)
D)