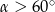Kąt  jest ostry i
jest ostry i 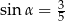 . Wtedy
. Wtedy
A) 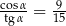 B)
B) 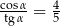 C)
C) 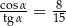 D)
D) 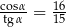
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna/Dany sinus
Dany jest kąt o mierze  taki, że
taki, że 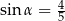 oraz
oraz 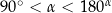 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla kąta o mierze  spełnione jest równanie: spełnione jest równanie: 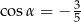 . . | P | F |
Dla kąta o mierze  spełnione jest równanie: spełnione jest równanie: 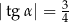 . . | P | F |
Kąt  jest ostry i
jest ostry i 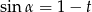 . Wtedy
. Wtedy
A) 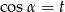 B)
B) 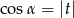 C)
C) 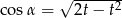 D)
D) 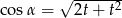
Kąt  jest ostry i
jest ostry i 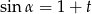 . Wtedy
. Wtedy
A) 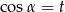 B)
B) 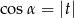 C)
C) 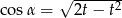 D)
D) 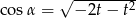
Kąt  jest ostry i
jest ostry i 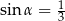 . Wartość wyrażenia
. Wartość wyrażenia 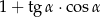 jest równa
jest równa
A) 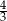 B)
B) 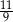 C)
C) 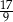 D)
D) 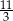
Kąt  jest ostry i
jest ostry i 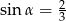 . Wartość wyrażenia
. Wartość wyrażenia 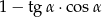 jest równa
jest równa
A) 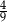 B)
B)  C)
C) 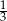 D)
D) 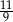
Jeżeli 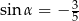 i
i 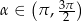 , to
, to
A) 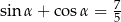 B)
B) 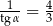 C)
C) 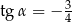 D)
D) 
Kąt  jest ostry i
jest ostry i 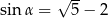 . Wartość wyrażenia
. Wartość wyrażenia 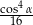 jest równa
jest równa
A) 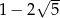 B)
B) 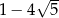 C)
C) 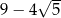 D)
D) 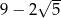
Kąt  jest ostry i
jest ostry i 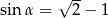 . Wartość wyrażenia
. Wartość wyrażenia 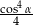 jest równa
jest równa
A) 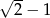 B)
B) 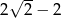 C)
C) 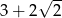 D)
D) 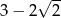
Kąt  jest ostry i
jest ostry i 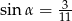 . Wówczas
. Wówczas 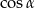 jest równy
jest równy
A) 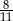 B)
B) 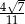 C)
C) 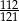 D)
D) 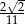
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 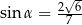 . Stąd wynika, że
. Stąd wynika, że
A) 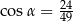 B)
B) 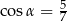 C)
C) 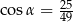 D)
D) 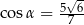
Kąt  jest ostry i
jest ostry i 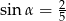 . Wówczas
. Wówczas 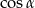 jest równy
jest równy
A)  B)
B) 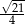 C)
C)  D)
D) 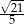
Sinusa kąta ostrego  jest równy 0,2. Cosinus kąta
jest równy 0,2. Cosinus kąta  jest równy
jest równy
A) 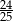 B)
B) 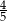 C)
C) 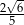 D)
D) 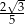
Sinus kąta ostrego  jest równy
jest równy  . Wtedy
. Wtedy
A) 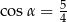 B)
B) 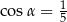 C)
C) 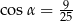 D)
D) 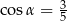
Kąt  jest ostry oraz
jest ostry oraz 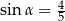 . Wtedy
. Wtedy
A) 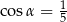 B)
B) 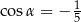 C)
C) 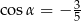 D)
D) 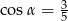
Kąt  jest ostry oraz
jest ostry oraz 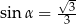 . Wtedy
. Wtedy
A) 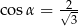 B)
B) 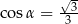 C)
C) 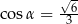 D)
D) 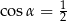
Sinus kąta ostrego  jest równy
jest równy  . Wówczas
. Wówczas
A) 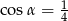 B)
B) 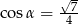 C)
C) 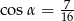 D)
D) 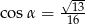
Sinus kąta ostrego  jest równy
jest równy 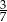 . Wówczas cosinus tego kąta jest równy
. Wówczas cosinus tego kąta jest równy
A) 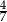 B)
B)  C)
C) 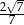 D)
D) 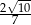
Kąt  jest ostry i
jest ostry i 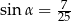 . Wynika stąd, że
. Wynika stąd, że
A) 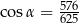 B)
B) 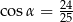 C)
C) 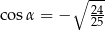 D)
D) 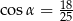
Sinus kąta ostrego  jest równy
jest równy 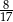 . Wówczas
. Wówczas
A) 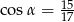 B)
B) 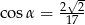 C)
C) 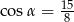 D)
D) 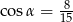
Jeśli wiadomo, że 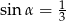 i
i  jest kątem ostrym, to prawdą jest, że
jest kątem ostrym, to prawdą jest, że
A) 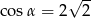 B)
B) 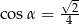 C)
C) 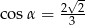 D)
D) 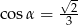
Kąt  jest ostry oraz
jest ostry oraz 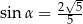 . Wtedy
. Wtedy
A) 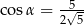 B)
B) 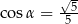 C)
C) 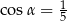 D)
D) 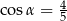
Kąt  jest ostry i
jest ostry i 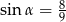 . Wówczas
. Wówczas 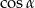 jest równy
jest równy
A) 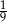 B)
B) 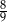 C)
C) 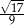 D)
D) 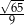
Kąt  jest ostry i
jest ostry i 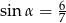 . Wówczas
. Wówczas 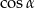 jest równy
jest równy
A) 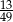 B)
B) 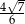 C)
C) 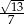 D)
D) 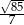
Kąt  jest ostry i
jest ostry i 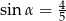 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 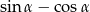 jest równa
jest równa
A) 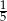 B)
B)  C)
C) 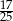 D)
D) 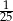
Kąt  jest ostry i
jest ostry i 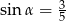 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 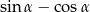 jest równa
jest równa
A) 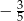 B)
B) 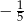 C)
C) 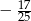 D)
D) 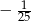
Jeśli dla kąta ostrego 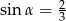 , to
, to
A) 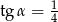 B)
B) 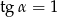 C)
C) 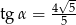 D)
D) 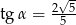
Jeśli dla kąta ostrego 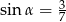 , to
, to
A) 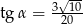 B)
B) 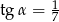 C)
C) 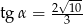 D)
D) 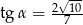
Kąt  jest ostry oraz
jest ostry oraz 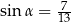 . Wtedy
. Wtedy 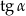 jest równy
jest równy
A)  B)
B) 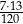 C)
C) 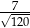 D)
D) 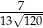
Wiadomo, że  jest kątem ostrym oraz
jest kątem ostrym oraz 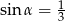 . Wówczas
. Wówczas
A) 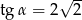 B)
B) 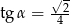 C)
C) 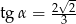 D)
D) 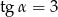
Jeśli dla kąta ostrego 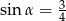 , to
, to
A) 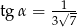 B)
B) 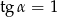 C)
C) 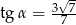 D)
D) 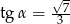
Kąt  jest ostry oraz
jest ostry oraz 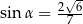 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 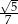 B)
B) 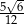 C)
C) 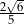 D)
D) 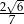
Sinus kąta ostrego  jest równy
jest równy 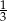 . Wówczas
. Wówczas 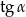 jest równy
jest równy
A) 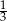 B)
B) 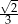 C)
C) 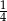 D)
D) 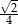
Kąt  jest ostry oraz
jest ostry oraz 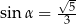 . Tangens kąta
. Tangens kąta  jest równy
jest równy
A) 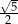 B)
B)  C)
C) 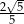 D)
D) 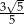
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 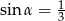 . Zatem
. Zatem
A) 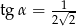 i
i 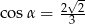
B) 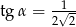 i
i 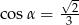
C) 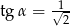 i
i 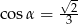
D) 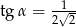 i
i 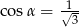
Jeżeli 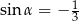 i
i 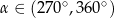 to
to
A) 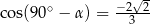 B)
B) 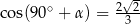
C) 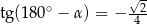 D)
D) 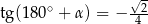
Jeżeli 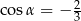 i
i 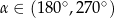 to
to
A) 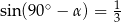 B)
B) 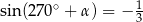
C) 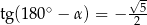 D)
D) 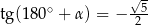
Kąt  jest ostry i
jest ostry i 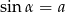 . Liczba
. Liczba  może być równa
może być równa
A) 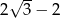 B)
B) 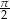 C)
C) 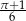 D)
D) 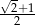
Kąt  jest ostry i
jest ostry i 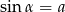 . Liczba
. Liczba  może być równa
może być równa
A) 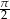 B)
B) 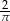 C)
C) 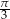 D)
D) 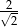
Kąt  jest rozwarty i spełniona jest równość
jest rozwarty i spełniona jest równość 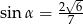 . Stąd wynika, że
. Stąd wynika, że
A) 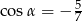 B)
B) 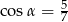 C)
C) 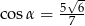 D)
D) 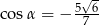
Wiadomo, że 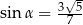 i
i 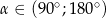 . Wynika stąd, że
. Wynika stąd, że
A) 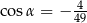 B)
B) 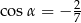 C)
C) 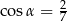 D)
D) 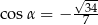
Kąt  jest rozwarty oraz
jest rozwarty oraz 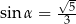 . Tangens
. Tangens  jest równy
jest równy
A) 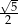 B)
B) 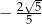 C)
C) 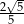 D)
D) 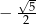
Sinus kąta rozwartego  jest równy
jest równy  . Wtedy
. Wtedy
A) 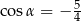 B)
B) 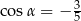 C)
C) 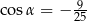 D)
D) 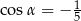
Jeżeli 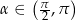 i
i 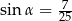 , to
, to
A) 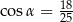 B)
B) 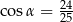 C)
C) 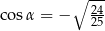 D)
D) 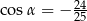
Jeśli  jest kątem ostrym i
jest kątem ostrym i 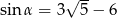 , to
, to 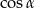 jest równy
jest równy
A) 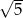 B)
B) 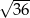 C)
C) 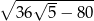 D)
D) 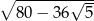
Jeśli  jest kątem ostrym i
jest kątem ostrym i 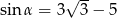 , to
, to 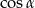 jest równy
jest równy
A) 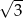 B)
B) 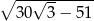 C)
C) 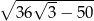 D)
D) 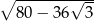
Jeśli  jest kątem ostrym i
jest kątem ostrym i 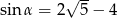 , to
, to 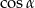 jest równy
jest równy
A) 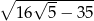 B)
B) 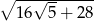 C)
C) 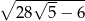 D)
D) 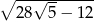
Kąt  jest ostry i
jest ostry i 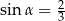 . Wtedy
. Wtedy 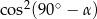 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 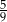
Kąt  jest ostry i
jest ostry i 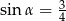 . Wartość wyrażenia
. Wartość wyrażenia 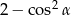 jest równa
jest równa
A) 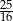 B)
B)  C)
C) 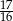 D)
D) 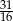
Kąt  jest ostry i
jest ostry i 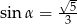 . Wartość wyrażenia
. Wartość wyrażenia 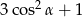 jest równa
jest równa
A)  B)
B) 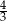 C)
C)  D)
D) 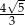
Kąt  jest ostry i
jest ostry i 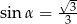 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 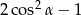 jest równa
jest równa
A) 0 B) 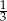 C)
C) 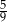 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 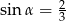 . Wartość wyrażenia
. Wartość wyrażenia 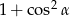 jest równa
jest równa
A) 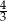 B)
B) 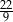 C)
C) 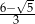 D)
D) 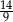
Kąt  jest ostry i
jest ostry i 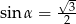 . Wartość wyrażenia
. Wartość wyrażenia 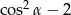 jest równa
jest równa
A) 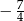 B)
B) 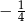 C)
C) 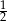 D)
D) 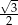
Kąt  jest ostry i
jest ostry i 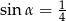 . Wówczas
. Wówczas
A) 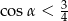 B)
B) 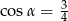 C)
C) 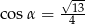 D)
D) 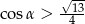
Kąt  jest ostry i
jest ostry i 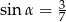 . Wówczas
. Wówczas
A) 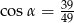 B)
B) 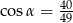 C)
C) 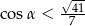 D)
D) 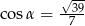
Jeśli 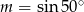 , to
, to
A) 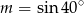 B)
B) 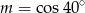 C)
C) 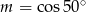 D)
D) 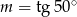
Jeśli 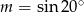 , to
, to
A) 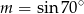 B)
B) 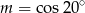 C)
C) 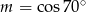 D)
D) 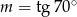
Kąt  jest ostry i
jest ostry i 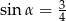 . Wówczas
. Wówczas
A) 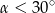 B)
B) 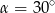 C)
C) 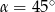 D)
D) 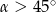
Kąt  jest ostry i
jest ostry i 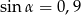 . Wówczas
. Wówczas
A) 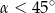 B)
B) 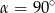 C)
C) 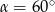 D)
D) 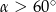
Kąt  jest ostry oraz
jest ostry oraz 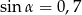 . Zatem
. Zatem
A) 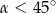 B)
B) 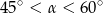 C)
C) 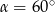 D)
D) 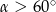
Jeśli  jest kątem ostrym i
jest kątem ostrym i 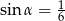 , to
, to
A) 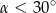 B)
B) 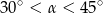 C)
C) 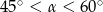 D)
D)