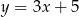Proste o równaniach: 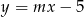 i
i 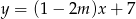 są równoległe, gdy
są równoległe, gdy
A) 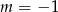 B)
B) 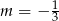 C)
C) 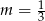 D)
D) 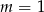
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Proste równoległe
Prosta 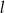 o równaniu
o równaniu 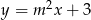 jest równoległa do prostej
jest równoległa do prostej 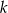 o równaniu
o równaniu 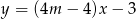 . Zatem
. Zatem
A) 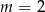 B)
B) 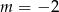 C)
C) 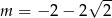 D)
D) 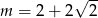
Proste o równaniach 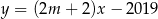 i
i 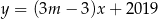 są równoległe, gdy
są równoległe, gdy
A) 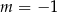 B)
B) 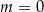 C)
C) 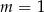 D)
D) 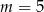
Proste o równaniach 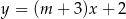 i
i 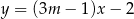 są równoległe, gdy
są równoległe, gdy
A) 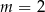 B)
B) 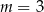 C)
C) 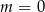 D)
D) 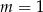
Proste o równaniach: 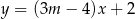 i
i 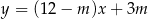 są równoległe, gdy
są równoległe, gdy
A) 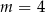 B)
B) 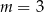 C)
C) 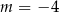 D)
D) 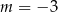
Proste o równaniach 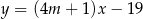 i
i 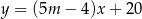 są równoległe, gdy
są równoległe, gdy
A) 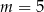 B)
B) 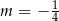 C)
C) 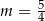 D)
D) 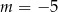
Prosta 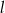 o równaniu
o równaniu 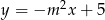 jest równoległa do prostej
jest równoległa do prostej 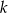 o równaniu
o równaniu 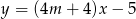 . Zatem
. Zatem
A) 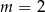 B)
B) 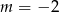 C)
C) 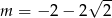 D)
D) 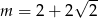
Proste 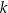 oraz
oraz 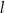 są określone równaniami
są określone równaniami
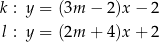
Proste 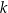 oraz
oraz 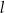 są równoległe, gdy liczba
są równoległe, gdy liczba 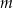 jest równa
jest równa
A) 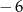 B)
B) 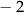 C) 2 D) 6
C) 2 D) 6
Proste o równaniach 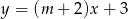 i
i 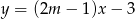 są równoległe, gdy
są równoległe, gdy
A) 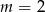 B)
B) 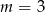 C)
C) 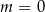 D)
D) 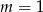
Proste 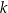 oraz
oraz 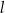 są określone równaniami
są określone równaniami
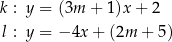
Proste 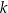 oraz
oraz 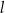 są równoległe, gdy liczba
są równoległe, gdy liczba 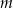 jest równa
jest równa
A) 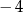 B)
B) 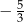 C)
C) 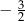 D)
D) 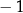
Prostymi równoległymi są wykresy funkcji liniowych:
A) 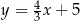 i
i 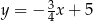 B)
B) 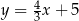 i
i 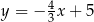
C) 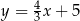 i
i 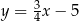 D)
D) 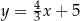 i
i 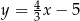
Dane są dwie proste równoległe 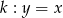 oraz
oraz 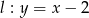 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 1,5 C) 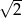 D) 1
D) 1
Odległość między prostymi 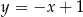 i
i 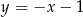 jest równa
jest równa
A) 2 B) 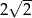 C) 1 D)
C) 1 D) 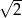
Dane są dwie proste równoległe 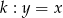 oraz
oraz 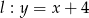 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 4 B) 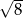 C)
C) 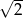 D) 3
D) 3
Dane są dwie proste równoległe 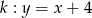 oraz
oraz 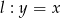 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 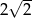 C)
C) 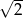 D) 4
D) 4
Odcinek o końcach 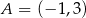 i
i 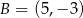 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu
A) 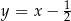 B)
B) 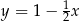 C)
C) 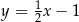 D)
D) 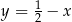
Prosta 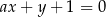 jest równoległa do prostej
jest równoległa do prostej 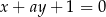 . Wtedy
. Wtedy
A) 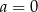 B)
B) 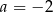 C)
C) 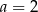 D)
D) 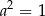
Prosta 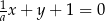 jest równoległa do prostej
jest równoległa do prostej 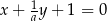 . Wtedy
. Wtedy
A) 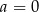 B)
B) 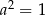 C)
C) 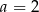 D)
D) 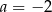
Prosta 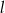 ma równanie
ma równanie 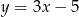 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 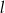 i przechodzącej przez punkt
i przechodzącej przez punkt 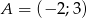 ma postać:
ma postać:
A) 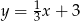 B)
B) 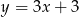 C)
C) 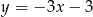 D)
D) 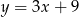
W kartezjańskim układzie współrzędnych 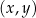 dana jest prosta
dana jest prosta 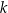 o równaniu
o równaniu 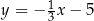 . Prosta o równaniu
. Prosta o równaniu 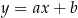 jest równoległa do prostej
jest równoległa do prostej 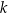 i przechodzi przez punkt
i przechodzi przez punkt 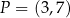 , gdy
, gdy
A) 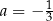 i
i 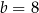 B)
B) 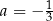 i
i 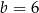 C)
C) 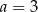 i
i 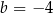 D)
D) 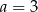 i
i 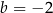
Prosta 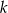 jest równoległa do prostej o równaniu
jest równoległa do prostej o równaniu 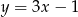 . Do wykresu prostej
. Do wykresu prostej 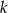 należy punkt
należy punkt 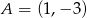 . Wskaż równanie prostej
. Wskaż równanie prostej 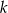 .
.
A) 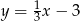 B)
B) 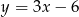 C)
C) 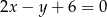 D)
D) 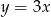
Równanie prostej równoległej do prostej 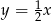 przechodzącej przez punkt
przechodzącej przez punkt 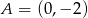 ma postać
ma postać
A) 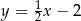 B)
B) 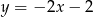 C)
C) 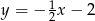 D)
D) 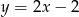
Dana jest prosta 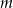 o równaniu
o równaniu 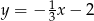 . Prosta
. Prosta 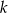 równoległa do prostej
równoległa do prostej 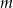 i przechodząca przez punkt
i przechodząca przez punkt 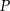 o współrzędnych
o współrzędnych 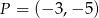 ma równanie
ma równanie
A) 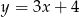 B)
B) 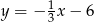 C)
C) 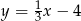 D)
D) 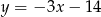
W kartezjańskim układzie współrzędnych 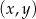 dana jest prosta
dana jest prosta 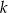 o równaniu
o równaniu 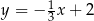 . Prosta o równaniu
. Prosta o równaniu 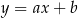 jest równoległa do prostej
jest równoległa do prostej 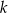 i przechodzi przez punkt
i przechodzi przez punkt 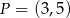 , gdy
, gdy
A) 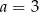 i
i 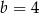 B)
B) 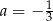 i
i 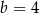 C)
C) 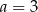 i
i 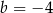 D)
D) 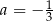 i
i 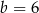
Prosta 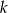 ma równanie
ma równanie 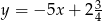 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 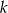 , przechodzącej przez punkt
, przechodzącej przez punkt 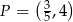 .
.
A) 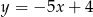 B)
B) 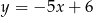 C)
C) 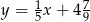 D)
D) 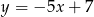
Prosta 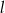 ma równanie
ma równanie 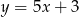 . Równanie prostej równoległej do prostej
. Równanie prostej równoległej do prostej 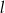 i przechodzącej przez punkt
i przechodzącej przez punkt 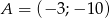 ma postać:
ma postać:
A) 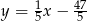 B)
B) 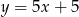 C)
C) 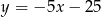 D)
D) 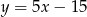
Prostą przechodzącą przez punkt 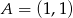 i równoległą do prostej
i równoległą do prostej 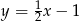 opisuje równanie
opisuje równanie
A) 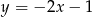 B)
B) 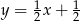 C)
C) 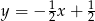 D)
D) 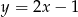
Prosta 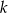 ma równanie
ma równanie 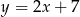 . Wskaż równanie prostej
. Wskaż równanie prostej 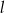 równoległej do prostej
równoległej do prostej 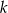 i przechodzącej przez punkt
i przechodzącej przez punkt 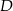 o współrzędnych
o współrzędnych 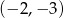 .
.
A) 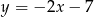 B)
B) 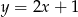 C)
C) 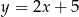 D)
D) 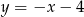
Prosta 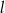 jest równoległa do prostej
jest równoległa do prostej 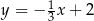 . Na prostej
. Na prostej 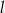 leży punkt
leży punkt 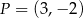 . Zatem równanie prostej
. Zatem równanie prostej 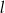 ma postać
ma postać
A) 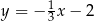 B)
B) 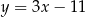 C)
C) 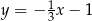 D)
D) 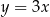
Dana jest prosta 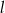 o równaniu
o równaniu 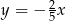 . Prosta
. Prosta 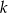 równoległa do prostej
równoległa do prostej 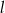 i przecinająca oś
i przecinająca oś 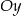 w punkcie o współrzędnych
w punkcie o współrzędnych 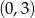 ma równanie
ma równanie
A) 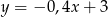 B)
B) 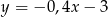 C)
C) 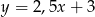 D)
D) 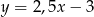
Równanie prostej przechodzącej przez punkt 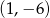 i równoległej do prostej
i równoległej do prostej 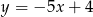 jest dane wzorem
jest dane wzorem
A) 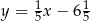 B)
B) 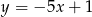 C)
C) 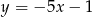 D)
D) 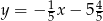
W kartezjańskim układzie współrzędnych 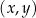 dane są prosta
dane są prosta 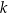 o równaniu
o równaniu 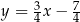 oraz punkt
oraz punkt 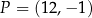 . Prosta przechodząca przez punkt
. Prosta przechodząca przez punkt 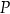 i równoległa do prostej
i równoległa do prostej 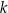 ma równanie
ma równanie
A) 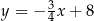 B)
B) 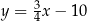 C)
C) 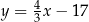 D)
D) 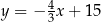
Prosta 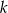 ma równanie
ma równanie 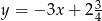 . Wskaż równanie prostej równoległej do prostej
. Wskaż równanie prostej równoległej do prostej 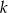 , przechodzącej przez punkt
, przechodzącej przez punkt 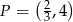 .
.
A) 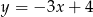 B)
B) 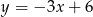 C)
C) 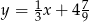 D)
D) 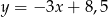
Prosta 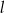 jest równoległa do prostej
jest równoległa do prostej 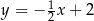 . Na prostej
. Na prostej 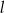 leży punkt
leży punkt 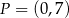 . Zatem równanie prostej
. Zatem równanie prostej 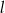 ma postać
ma postać
A) 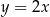 B)
B) 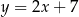 C)
C) 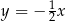 D)
D) 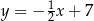
Prosta 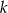 ma równanie
ma równanie 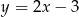 . Wskaż równanie prostej
. Wskaż równanie prostej 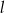 równoległej do prostej
równoległej do prostej 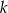 i przechodzącej przez punkt
i przechodzącej przez punkt 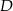 o współrzędnych
o współrzędnych 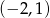 .
.
A) 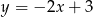 B)
B) 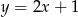 C)
C) 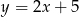 D)
D) 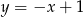
Prosta o równaniu 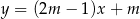 nie przecina prostej o równaniu
nie przecina prostej o równaniu 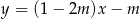 . Zatem
. Zatem
A) 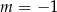 B)
B) 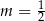 C)
C) 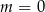 D)
D) 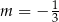
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 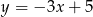 jest równy
jest równy
A) 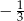 B) -3 C)
B) -3 C) 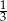 D) 3
D) 3
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 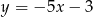 jest równy
jest równy
A) 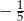 B) 5 C)
B) 5 C) 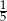 D) -5
D) -5
Prosta 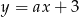 jest równoległa do prostej
jest równoległa do prostej 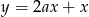 . Wtedy
. Wtedy
A) 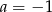 B)
B) 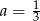 C)
C) 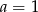 D)
D) 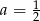
Prosta 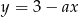 jest równoległa do prostej
jest równoległa do prostej 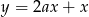 . Wtedy
. Wtedy
A) 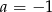 B)
B) 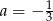 C)
C) 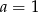 D)
D) 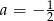
Prosta 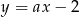 jest równoległa do prostej
jest równoległa do prostej 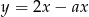 . Wtedy
. Wtedy
A) 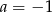 B)
B) 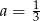 C)
C) 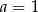 D)
D) 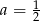
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 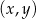 , dane są punkty
, dane są punkty 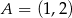 i
i 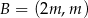 , gdzie
, gdzie 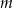 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 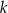 o równaniu
o równaniu 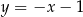 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 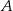 i
i 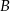 jest równoległa do prostej
jest równoległa do prostej 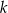 , gdy
, gdy
A) 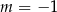 B)
B) 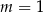 C)
C) 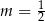 D)
D) 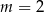
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 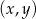 , dane są punkty
, dane są punkty 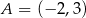 i
i 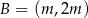 , gdzie
, gdzie 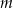 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 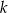 o równaniu
o równaniu 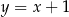 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 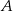 i
i 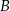 jest równoległa do prostej
jest równoległa do prostej 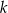 , gdy
, gdy
A) 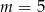 B)
B) 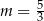 C)
C) 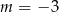 D)
D) 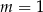
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 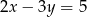 jest równy
jest równy
A) 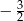 B)
B)  C)
C)  D) 2
D) 2
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 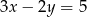 jest równy
jest równy
A) 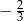 B)
B)  C)
C)  D)
D) 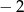
Proste o równaniach: 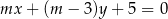 i
i 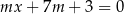 są równoległe, gdy
są równoległe, gdy
A) 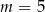 B)
B) 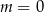 C)
C) 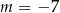 D)
D) 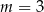
Proste o równaniach: 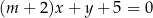 i
i 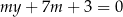 są równoległe, gdy
są równoległe, gdy
A) 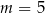 B)
B) 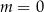 C)
C) 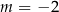 D)
D) 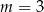
Proste o równaniach 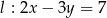 i
i 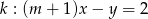 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 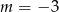 B)
B) 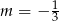 C)
C) 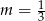 D)
D) 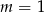
Proste o równaniach 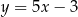 oraz
oraz 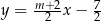 są równoległe, gdy
są równoległe, gdy
A) 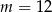 B)
B) 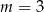 C)
C) 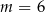 D)
D) 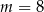
Dana jest prosta 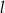 o równaniu
o równaniu 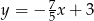 . Prosta
. Prosta 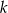 o równaniu
o równaniu 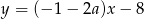 jest równoległa do prostej
jest równoległa do prostej 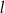 . Wynika stąd, że
. Wynika stąd, że  wynosi
wynosi
A) 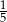 B)
B) 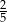 C) 2 D)
C) 2 D) 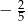
Proste o równaniach 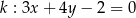 i
i 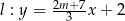 są równoległe, gdy
są równoległe, gdy
A) 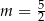 B)
B) 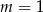 C)
C) 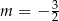 D)
D) 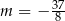
Proste o równaniach 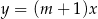 oraz
oraz 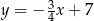 są równoległe. Wtedy
są równoległe. Wtedy
A) 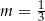 B)
B) 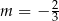 C)
C) 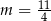 D)
D) 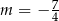
Proste o równaniach 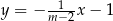 i
i 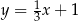 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 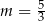 B)
B) 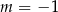 C)
C) 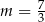 D)
D) 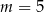
Dane są proste 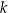 i
i 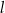 o równaniach
o równaniach
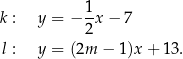
Proste 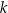 oraz
oraz 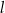 są równoległe, gdy
są równoległe, gdy
A) 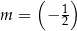 B)
B) 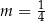 C)
C) 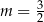 D)
D) 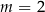
Proste o równaniach 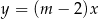 oraz
oraz 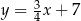 są równoległe. Wtedy
są równoległe. Wtedy
A) 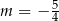 B)
B) 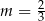 C)
C) 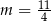 D)
D) 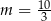
Proste o równaniach 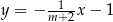 i
i 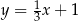 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 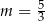 B)
B) 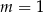 C)
C) 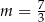 D)
D) 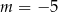
Proste o równaniach 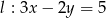 i
i 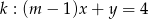 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 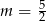 B)
B) 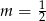 C)
C) 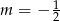 D)
D) 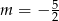
Dane są proste 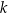 i
i 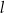 o równaniach
o równaniach
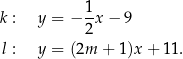
Proste 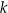 oraz
oraz 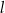 są równoległe, gdy
są równoległe, gdy
A) 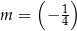 B)
B) 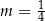 C)
C) 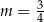 D)
D) 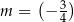
Proste o równaniach 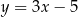 oraz
oraz 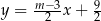 są równoległe, gdy
są równoległe, gdy
A) 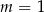 B)
B) 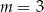 C)
C) 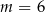 D)
D) 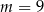
Proste o równaniach 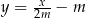 i
i 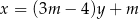 są równoległe, gdy
są równoległe, gdy
A) 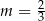 B)
B) 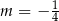 C)
C) 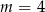 D)
D) 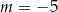
Prosta 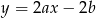 jest równoległa do prostej
jest równoległa do prostej 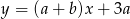 , gdzie
, gdzie 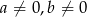 . Wynika stąd, że
. Wynika stąd, że
A) 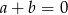 B)
B) 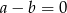 C)
C) 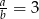 D)
D) 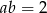
Prosta 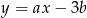 jest równoległa do prostej
jest równoległa do prostej 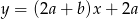 , gdzie
, gdzie 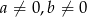 . Wynika stąd, że
. Wynika stąd, że
A) 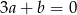 B)
B) 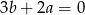 C)
C) 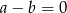 D)
D) 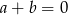
Prosta 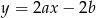 jest równoległa do prostej
jest równoległa do prostej 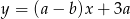 , gdzie
, gdzie 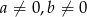 . Wynika stąd, że
. Wynika stąd, że
A) 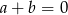 B)
B) 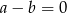 C)
C) 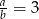 D)
D) 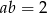
Odległość pomiędzy prostymi równoległymi 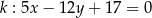 i
i 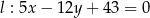 jest równa
jest równa
A) 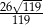 B)
B) 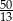 C) 1 D) 2
C) 1 D) 2
W kartezjańskim układzie współrzędnych 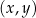 dana jest prosta
dana jest prosta 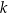 o równaniu
o równaniu 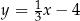 . Prosta o równaniu
. Prosta o równaniu 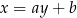 jest równoległa do prostej
jest równoległa do prostej 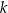 i przechodzi przez punkt
i przechodzi przez punkt 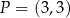 , gdy
, gdy
A) 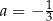 i
i 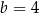 B)
B) 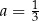 i
i 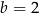 C)
C) 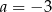 i
i 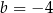 D)
D) 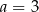 i
i 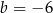
Prostą równoległą do prostej 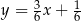 jest prosta:
jest prosta:
A) 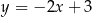 B)
B) 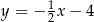 C)
C) 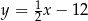 D)
D) 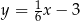
Prosta o równaniu 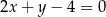 jest równoległa do prostej:
jest równoległa do prostej:
A) 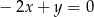 B)
B) 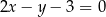 C)
C) 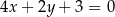 D)
D) 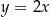
Wskaż równanie prostej równoległej do prostej o równaniu 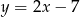 .
.
A) 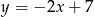 B)
B) 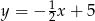 C)
C) 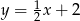 D)
D) 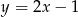
Prosta równoległa do prostej 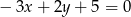 ma równanie:
ma równanie:
A) 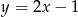 B)
B) 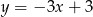 C)
C) 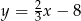 D)
D) 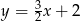
Wskaż równanie prostej równoległej do prostej o równaniu 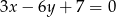 .
.
A) 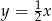 B)
B) 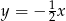 C)
C) 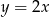 D)
D) 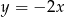
Prostą równoległą do prostej o równaniu 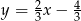 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 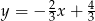 B)
B) 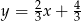 C)
C) 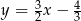 D)
D) 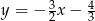
Prosta 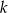 równoległa do prostej
równoległa do prostej 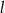 o równaniu
o równaniu 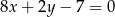 może mieć wzór
może mieć wzór
A) 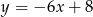 B)
B) 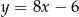 C)
C) 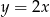 D)
D) 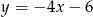
Prosta 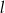 ma równanie
ma równanie 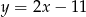 . Wskaż równanie prostej równoległej do
. Wskaż równanie prostej równoległej do 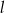 .
.
A) 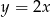 B)
B) 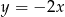 C)
C) 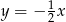 D)
D) 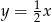
Wskaż równanie prostej równoległej do prostej o równaniu 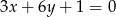 .
.
A) 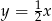 B)
B) 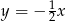 C)
C) 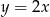 D)
D) 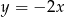
Prostą równoległą do prostej o równaniu 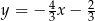 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 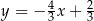 B)
B) 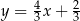 C)
C) 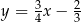 D)
D) 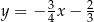
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 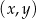 , dana jest prosta
, dana jest prosta 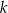 o równaniu
o równaniu 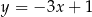 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 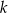 jest prosta o równaniu
jest prosta o równaniu
A) 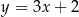 B)
B) 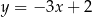 C)
C) 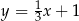 D)
D) 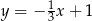
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 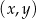 , dana jest prosta
, dana jest prosta 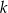 o równaniu
o równaniu 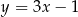 . Jedną z prostych równoległych do prostej
. Jedną z prostych równoległych do prostej 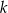 jest prosta o równaniu
jest prosta o równaniu
A) 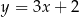 B)
B) 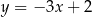 C)
C) 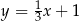 D)
D) 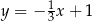
Dana jest prosta 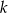 o równaniu
o równaniu 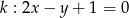 . Spośród podanych prostych wybierz prostą równoległą do
. Spośród podanych prostych wybierz prostą równoległą do 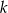 .
.
A) 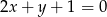 B)
B) 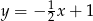 C)
C) 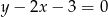 D)
D) 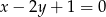
Prostą równoległą do prostej 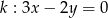 opisuje równanie
opisuje równanie
A) 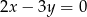 B)
B) 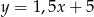 C)
C) 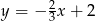 D)
D)